最长子串、子序列

先说明下子串和子序列的问题：对于s = “pwwkew"来说，其中一个子串为"wke”，而"pwke" 是一个子序列。
子序列：一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。
对于求最长子串、最长序列的问题：
基本上需要用到动态规划的dp数组来辅助。主要原因是，如果暴力求各个子串或者序列的话，算数量太大，容易超时。
在使用dp数组时，有两种类型，一种是一维的dp数组，一种是二维的dp数组。

一维dp

对于一个字符串或者数组中求最大值时，一般考虑一维的dp数组，并且对于其定义为dp[i]表示为从S[0]到S[i]间符合题意的最大值。但如果用这个定义会导致转移状态方程不好推导，dp[i]和dp[i-1]中间有断层，则需要考虑更改dp[i]的定义。可以考虑把dp[i]表示为以S[i]为结尾的子串或者子数组的符合题意的最大值，比如力扣如下题：

有断层

对于有断层的，一般都要在推导dp[i]时，需要在0 ~ i -1间找到一个最大的，来推导dp[i]。

最长递增子序列

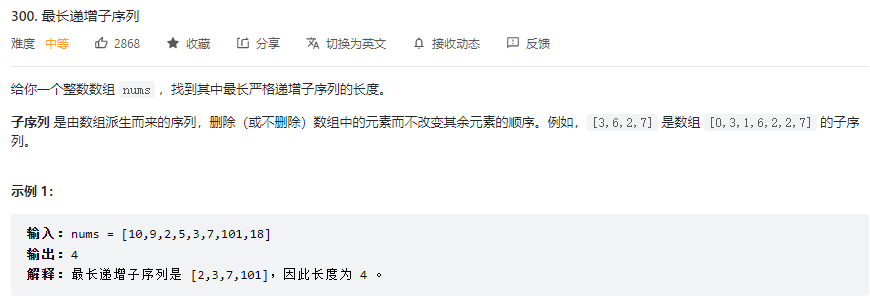
对于dp数组的定义：
这个题是有断层的。如果把dp[i]定义为，nums[0 … i]子数组中的最长递增子序列的长度，那么当第i个元素要加入时，就会出现问题，如下图所示，当前nums[i]不好去找dp[i-1]的元素去比较，从而推导出dp[i]。此时需要更换对于dp[i]的定义。

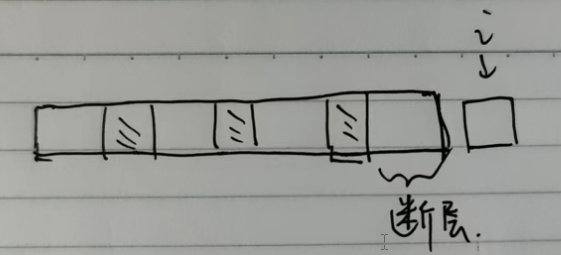
当我们把dp[i]定义为：以nums[i]为结尾的子数组的最长递增子序列的长度。那么断层就不会出现，dp[i-1]中的子数组，永远会包含nums[i-1]自己。如下图：

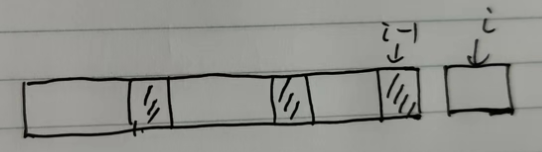
那么我们就在比较dp[i]和dp[i-1]的大小，就能推导出dp[i]的值。也需要一种逆向思维，从转移公式开始去推导对dp[i]定义的修改。
对于dp数组的转移公式：
当我们要求dp[i]时，即需要把nums[i]插入进去。那么它应该在哪个位置比较合适呢？
这里最关键，如果不加思考，可能会觉得如果nums[i] > nums[i - 1]的话，就让dp[i] = dp[i -1] + 1。这里有个问题，就是原nums数组并不是有序的，你不能确保dp[i -1]就是dp[0] ~ dp[i -1]里头最大的那个啊！nums[i] < nums[i - 1]时的操作也一样。
最直观的方式就是，从i-1往前找，找到一个nums[j]小于等于nums[i]的，并且dp[j]是当中最大的，这样就可以推导出dp[i]了，因为dp[i]一定包含自己，那是否要包含[0 ~ i-1]中的元素，那就得去找到一个满足值小于自己的，并且dp又是最大的来计算。
另外，这里找到这么一个j后，还要看nums[j]是否与nums[i]，相等，如果相等，那么dp[i] = dp[j]；不相等（肯定是小于nums[i]的），则dp[i] = dp[j] + 1。

最大子数组和

对于dp[i]的定义为：以nums[i]为结尾的「最大子数组和」

无重复字符的最长子串

如果定义dp[i]为：s[0 … i]的【无重复字符的最长子串】的长度，那么就会有断层，我并不知道dp[i - 1]表示的那个满足题意的连续子串的位置在哪里，这样我也不好去推导dp[i]出来。如下图：

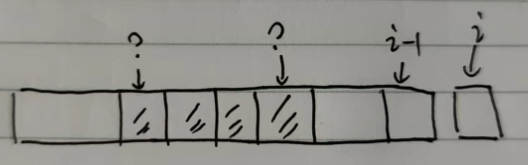
所以必须针对这个断层，修改定义。对于dp[i]的定义为：以s[i]为结尾的【无重复字符的最长子串】的长度。
在推导dp[i]时，需要去检测从start开始到i-1，处是否有nums[i]这个元素，对于dp[i]的值应该是从i-1开始到第一个出现nums[i]元素间的距离。

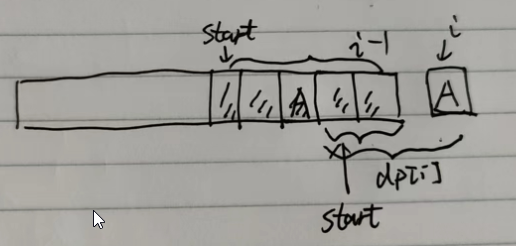
注意：这里需要使用一个pair<int, int>记录前一个dp[i]的最长子串的始末位置，在判断s[i]与s[i-1]不等时，需要继续往前判断s[i]是否包含在前一个dp[i-1]的子串中，如果在，则当前的dp[i]需要减去dp[i-1]子串的前一部分。

买卖股票的最佳时机

• 定义推导
  这里如果定义dp[i]为[0 … i]里最大收益，那么同样是会出现断层，即买卖点不知道在哪里。这个时候我们一定要确定一个卖点时间。那么自然会把dp[i]定义为：第i天卖出股票能获得的最大收益。
• 状态转移方程推导：
  这里如果按照前面的方式会进入一个误区，就是dp[i]由dp[i-1]来计算出来。但是你并不知道dp[i-1]是在哪天买入的。这里有一个非常重点的东西就是，收益最大，那么一定要买入价格最低，反正我都必须在第i天卖出。那就扫描数组的时候记录下[0 ~ i-1]区间里的最小值即可。
  dp[i] = prices[i] - minPrices; 再注意更新下minPrices即可。

二维dp

如果涉及到两个字符串或者数组的，基本上需要用到二维dp数组。对于二维dp的状态转移方程，大致都会是要从左、上及左上三个方向来推导，即：dp[i][j] = max(dp[i-1][j], dp[i][j-1], dp[i-1][j-1])。

• 1143. 最长公共子序列
        
        这里对于dp的定义需要使用到二维数组，因为这里涉及到两个字符串。
        定义dp[i][j]为：s1[0…i-1]及s2[0…j-1]两个字符串的【最长公共子序列】的长度。
        dp[0][x]/dp[x][0]表示其中有一个是空字符串，那它们的最长公共子序列的长度自然为0；
        转移方程：dp[i][j] = max(dp[i-1][j], dp[i][j-1], dp[i-1][j-1])
• 516. 最长回文子序列
       
       定义dp[i][j]为：s[i … j]之间的最长回文子序列的长度。
       那么dp[i][j]要从dp[i+1][j-1]、dp[i][j-1]、dp[i+1][j]三者中取出。
       当s[i] == s[j]时，比较简单，显然dp[i][j] = d[i+1][j-1] + 2
       当s[i] != s[j]时，说明s[i]和s[j]不能同时出现在s[i…j]的最长回文子序列中。那么就只能在s[i]或者s[j]中取一个去加入到上一个回文子序列中，形成新的回文子序列。即dp[i][j] = max(dp[i][j-1], dp[i+1][j])