Description

小J学习了等差数列，于是他很开心的知道了

1+2+3+.....+100=5050.

现在他想知道，对于某个公差为1的等差数列，如果总和为N的话。

有多少个等差数列满足这个条件

Format

Input

一行给出整数N

N<=10^12

Output

一行给出你的结果

Samples

输入数据 1

12

Copy

输出数据 1

4

Copy

输入数据 2

1

Copy

输出数据 2

2

Copy

Hint 对于样例存在以下四种数列

[12]

[3,4,5]

[−2,−1,0,1,2,3,4,5]

[−11,−10,−9,…,10,11,12]

---

思路:

 

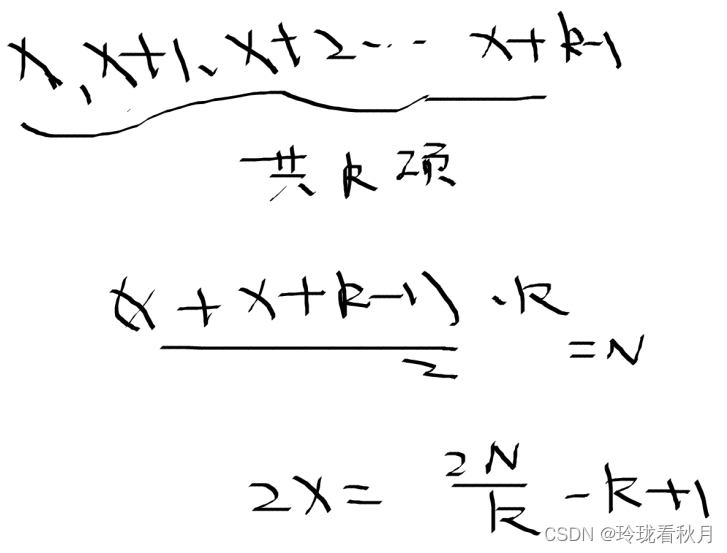
 于是枚举K，明显K应该为2N的约数，代入上式算出2n/k-k+1,这个数字必须为偶数

同理如果k是2N的约数，则另一个约数为2n/k....

当然k如果等于2n/k，则只能算一次。 

记得开long long ，为什么要开，自己想清楚。。。。。

---

#include <bits/stdc++.h>
using namespace std;
#define int long long
int s,n,t;
signed main()
{
  cin>>n;
  n *= 2;
  for(int k = 1; k <= n / k; k++)
    if(n % k == 0)
    {
      t = n / k - k + 1;
      if(t % 2 == 0) s++;
      int kk = n / k;
      if(k == n / k) continue;
      t = n / kk - kk + 1;
      if(t % 2 == 0) s++;
    }
  cout<<s;
  return 0;
}