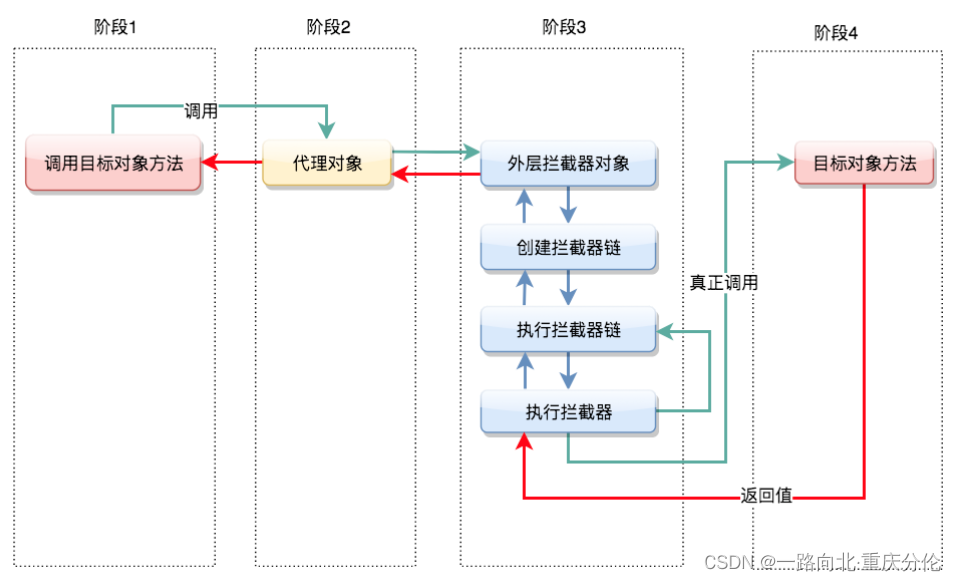
叉乘的定义：

混合积的几何意义：就是平行六面体的体积

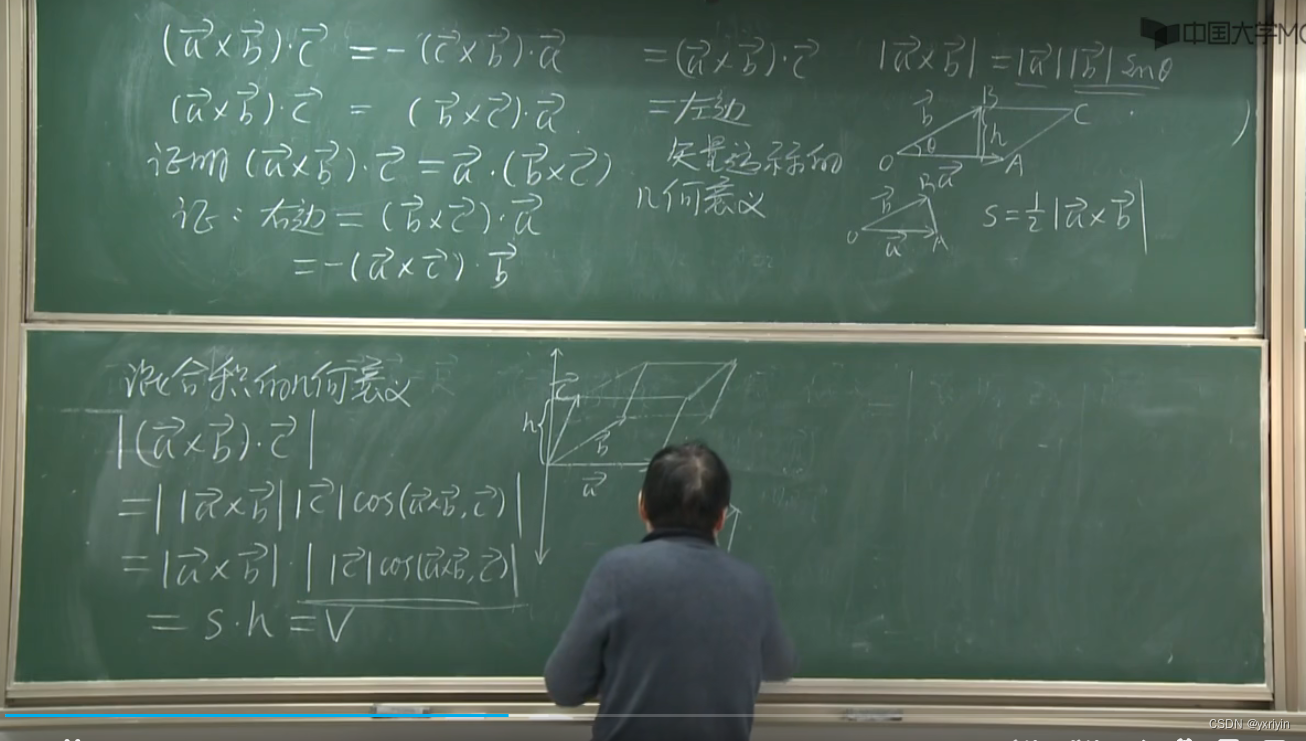
 三个向量共面的充要条件：

 这里要注意，混合机对应的就是三阶行列式的值。

平面方程：

点法式：

 一般式：

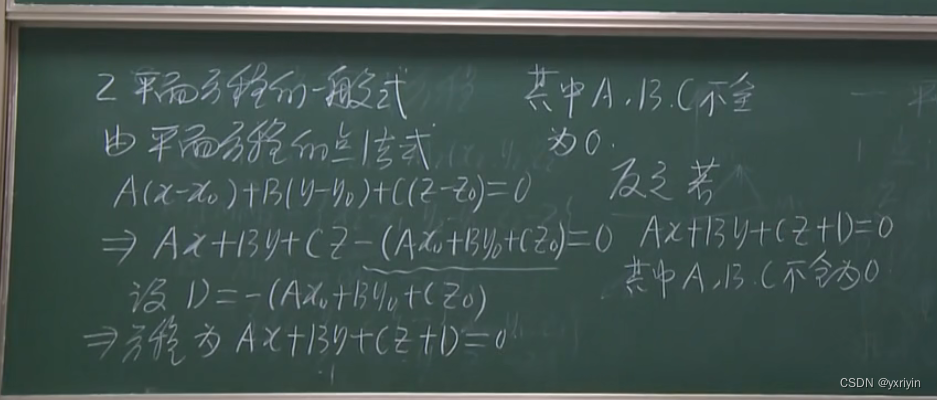
截距式：

三点式：

直线方程

点向式：

 参数式：

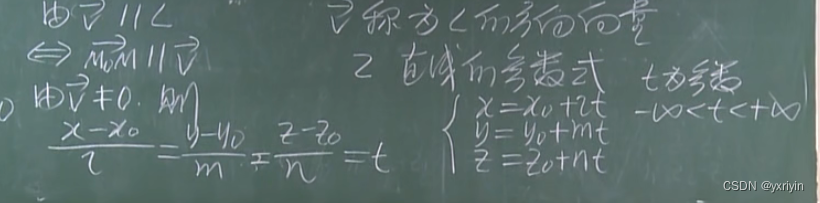
两点式：

一般式：

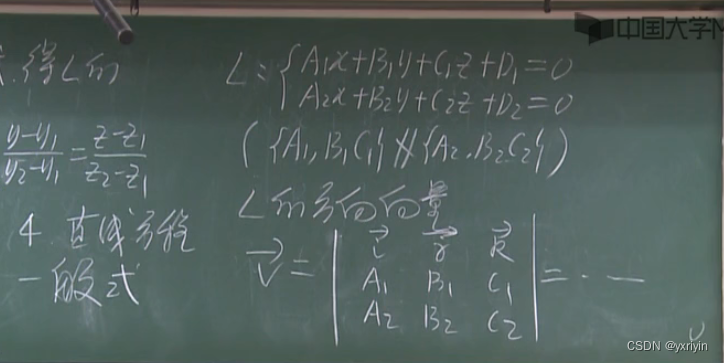
点到平面的距离：

点到直线的距离：

其他空间解析几何暂时不列举了，需要的时候再复习好了。

接下来是重点 多元函数微分学和积分学。

判断二元函数极限不存在的方法：

 多元函数的连续：

 全增量和偏增量：

偏导数的定义：

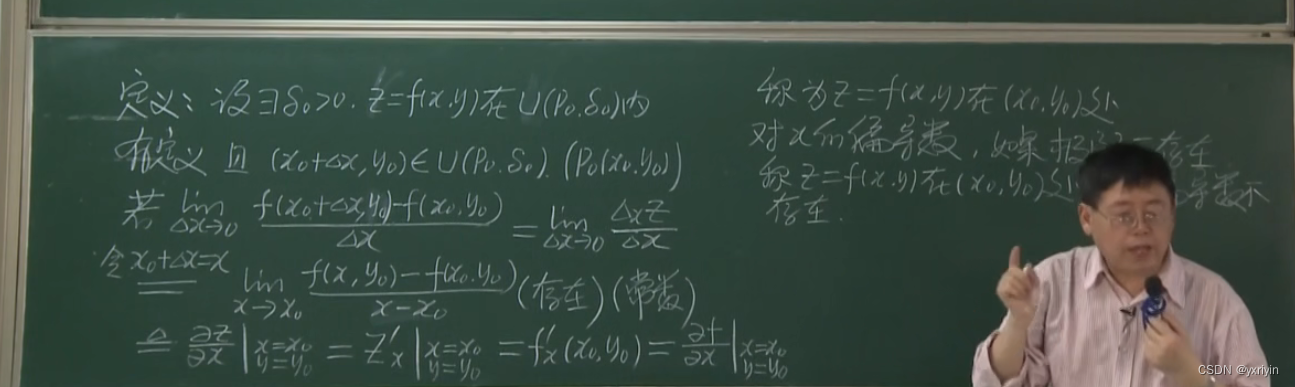
 多重偏导和顺序无关：

证明：

不要求，用四次拉格朗日定理 

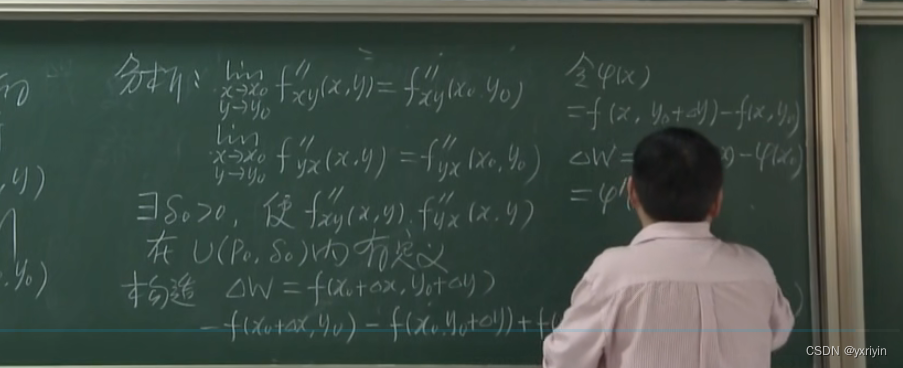
全微分的定义：

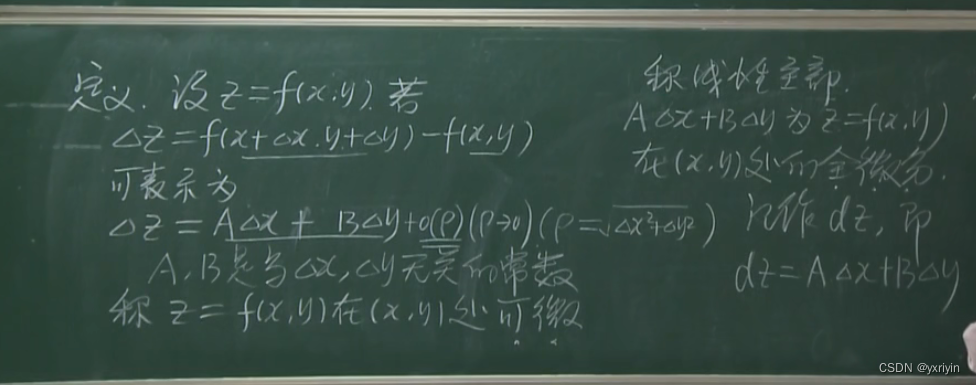
这里要注意，虽然是定义，但这个定义可以推倒出来的：

按照《简明微积分》里面的推倒：

=f(x+,y+)-f(x,y)

     =f(x+,y+)-f(x,y+y) +f(x,y + y)-f(x,y)

用微分中值定理：

    =(x+,y+) + 

 当增量x,y都趋向于0的时候，

对于高阶无穷小量的说明，我们来看：

从理解上说，p=  和之前单个变量的距离是一致的。

按照一元变量的定义：

所以

于是

后面的就是的高阶无穷小。

对于多元微积分来说，下面的分母应该就是自变量改变量的距离，一般我们对距离的定义就是

常规的

高阶无穷小量p的另一种表示形式：

那么我们怎么证明A就是z对x的偏导呢？

令这个时候，

那么

于是

同理可证明B

复合偏导数求导法则证明：

图中有笔误，z误写成了u，理解就好

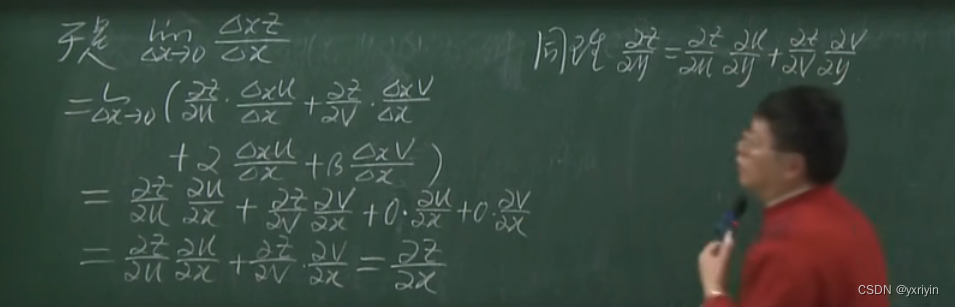
全微分一阶形式不变性的证明：

 方程确定多元函数求偏导的方法：

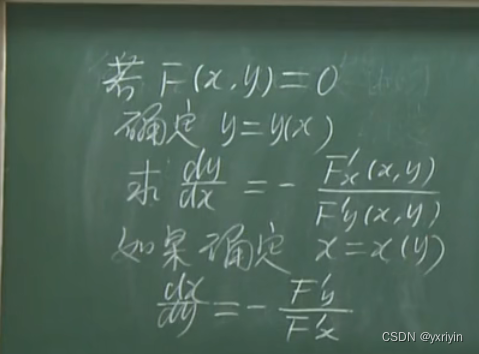
可以复习下克拉默法则：

克拉默法则是怎么想出来的？ - 知乎

方向导数定理：

证明：

 梯度：

几何意义：

 梯度是方向导数中最大的一个。

拉格朗日数乘法：

二重积分：

非规则区域的和式极限为0（边界曲线的面积为0）

二重积分的计算：

把二重积分化成累次积分

 

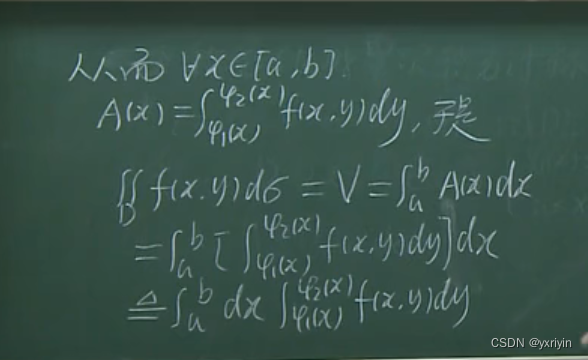
二重积分换元，引出了雅克比行列式，

这里我们看《简明微积分》里面的证明：

书上有点笔误，知乎上有个简略证明：重积分换元的公式，证明，解法，例题 - 知乎

我们也简单证明下：

 图还是按照这个图，证明按照《简明微积分》

取四个点，M1,M2,M3,M4

坐标分别为：

M1:x1,y1

M2:x1 +  + o(p), y1 +  + o(p)

M3:可以忽略

M4:x1 +  + o(p), y1 +  + o(p)

因爲近似成平行四边形，所以直接取两相邻的边叉乘即可。

M1M2:  + o(p),  + o(p)

M1M4: + o(p),  + o(p)

根据叉乘公式：

就是（  + o(p)）（  + o(p)）-（  + o(p)）（  + o(p)）

展开：

​​​​​​​

知乎上是没有这个高阶无穷小的项的，但我觉得简明微积分里的更加正确，只有加了d的微分才可以舍弃高阶无穷小，而上面这个是等于号，我认为不能舍弃高阶无穷小。

让我们重新梳理思路：

首先，从体积的角度去理解这个二重积分：

就是对于区域D下的面积，和每个微元的函数值的积分，最终形成体积的概念。就是求和公式：

而通过换元u,v, f(x(u,v),y(u,v)) 可以看成复合函数f(T(u,v))

还是从求和公式出发先：

核心就在于求和公式中和的区别

我认为简明微积分的做法更加正确。

首先毫无疑问，从单变量微积分讲，dx=f'(u)du

这是因为自变量u的改变量du会引起因变量dx的改变量，它近似与f'(u)du，当du趋于0时，可以把高阶无穷小（相对于du）舍去，也就是直接等于。

类比到二元微积分中，就是因变量dxdy=Adudv

因为是两个变量，几何上要从一维的长度变成二维的面积。

注意，其实dxdy和dudv应该是一个整体，只是进行积分计算的时候，我们可以化成累次积分。

所以考虑uv下的自变量的改变量d,它引起的因变量的改变量d',我们可以画图：

也就是四个点，A(x(u,v),y(u,v),  B(x(u+du, v), y(u+du), v)

                         C(x(u,v+dv),y(u,v+dv)),  D（坐标忽略）

这个新的四边形的面积就是因变量的改变量。

我们用叉乘算出面积：

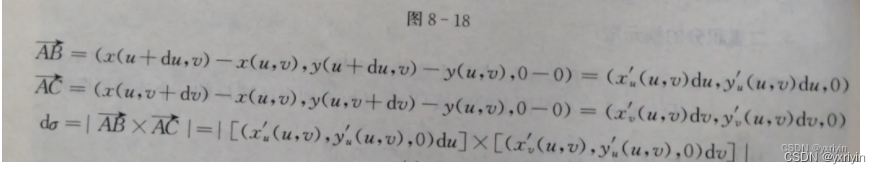
至于为什么二元是面积的变化，包括更高维度怎么处理，我们需要去学习卓里奇的数学分析再看了。