目录

逆波兰表达式

四元式

三元式

间接三元式

---

逆波兰表达式

逆波兰表示法即后缀表达式，而后缀表达式需要注意：

①遵循从外向内进行分析

②由算数优先符从低到高进行拆分，例如：

我们以“-”号作为分隔进行拆分，而不是以“*”号

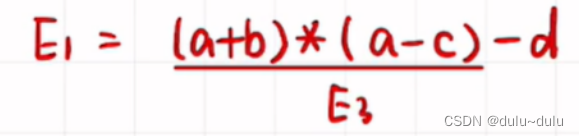
来看一个例题

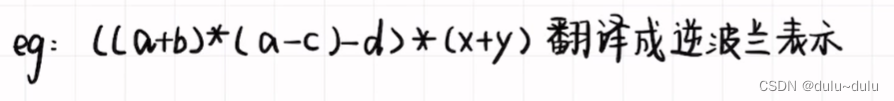首先

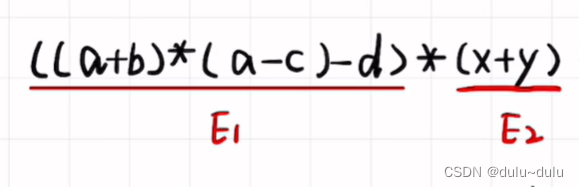
原式子：E1*E2        变为后缀表达式：E1E2*，同理可得：

最终，将分解的式子带回：

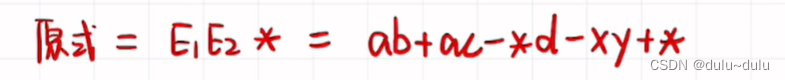
再举一个例子：

①a-(-b)*c=aE1-

②E1=（-b）*c= (-b) c* = b @ c *（求负运算表示为@）

③后缀表达式=a b @ c * -

含有布尔运算符的逆波兰表达式：

四元式

四元式和逆波兰表达式的过程相反，是由内到外进行计算：

第一步是*，参与运算的符号是B,D，命名为t1，以此类推

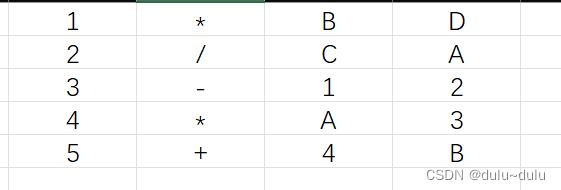
三元式

三元式与四元式对比，如下：

将四元式的最后一列去掉，并且将t4 转为 4

间接三元式

如下图所示的四元式中（1）和（4）重复了

可以将（4）去掉，而其后的（5），（6），（7）就变为（4），（5），（6）

原式中的（5）（^ (4) N）,则为（4）（^ （1）N）