前言
前几期我们详细介绍了插入排序(直接插入排序和希尔排序)、选择排序(直接选择和堆排序)、交换排序(冒泡排序和快速排序)。并对快排的各个版本做了详细的介绍,本期我们来介绍把最后两个即外部排序:归并排序 和 非比较:计数排序。
本期内容介绍
归并排序递归版
归并排序非递归版
计数排序
归并排序
归并排序递归版
基本思路:将两个有序的子序列合并成一个有序的序列的过程~!
具体过程:将一个无序的序列分成两个长度相等或相差1 的两个左右子序列,分别对左右的两个子序列重复上述操作,直到只有一个元素,开始往回归并即取较小的尾插~!一组归并完了拷贝回原数组,再去归并另一组,直至整个序列有序~!由于数组不像链表可以直接拿下来,所以得借助一个第三方的辅助空间~!
OK,干说理论可能不太清楚我来画个图理解一下:
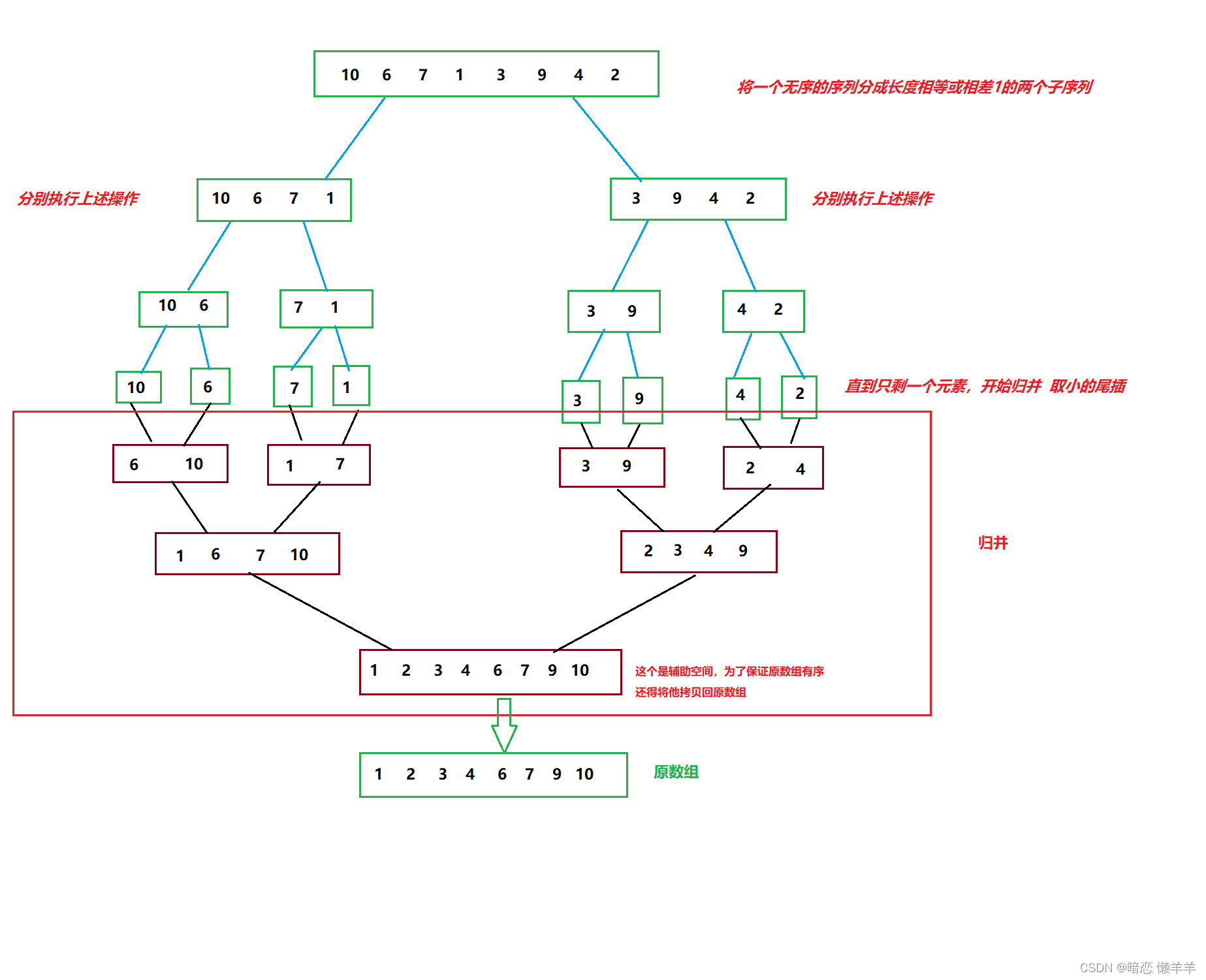
这就是一个归并的过程,但注意的是,他的分割不是又生成新的小数组,而是通过下标控制的!下面的归并也是,不是每次归并就开一个对应大小的数组而是一开始就开一个和原数组一样大的,通过下标的控制即可~!有没觉得这个和前面二叉树的那个后序遍历相似!
所以上面的图实际上是下面这样:

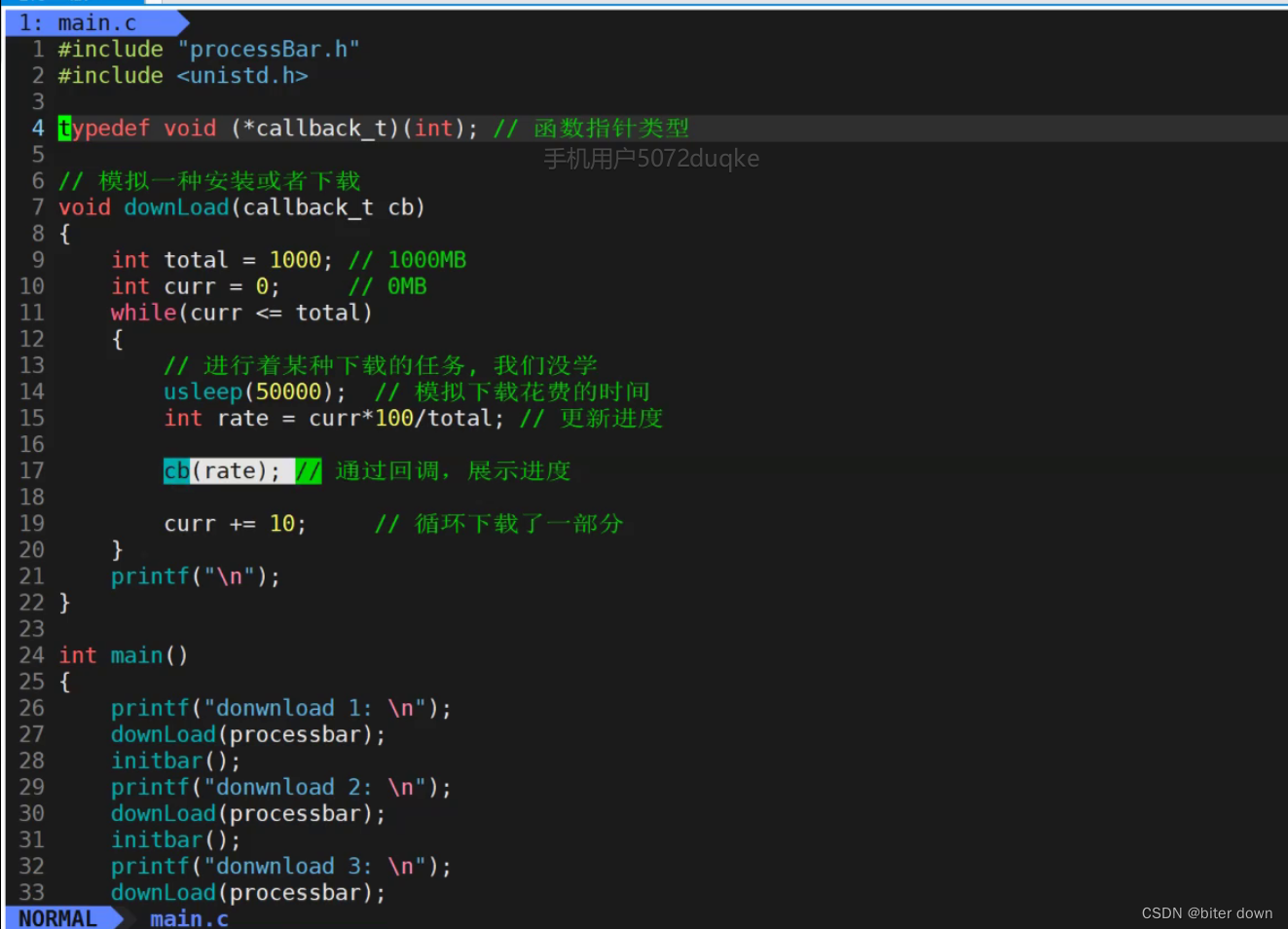
OK,上代码
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);//辅助空间
if (NULL == tmp)
{
perror("malloc failed");
exit(-1);
}
_MergeSort(a, tmp, 0, n - 1);
free(tmp);
}这里为了不每次归并都开空间,我们一开始先开好,然后以以参数的形式传过去~!
void _MergeSort(int* a, int* tmp, int begin, int end)
{
if (begin >= end)//只有一个或越界时不要再分了
return;
int mid = begin + (end - begin) / 2;//找中间的位置
_MergeSort(a, tmp, begin, mid);//分割左区间
_MergeSort(a, tmp, mid + 1, end);//分割右区间
int begin1 = begin, end1 = mid;//左区间的开始和结束
int begin2 = mid + 1, end2 = end;//右区间的开始和结束
int index = begin;//开始归并的辅助空间的起始位置就是当前区间的开始位置
while (begin1 <= end1 && begin2 <= end2)//归并
{
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
//把剩余的放在后面
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
//拷贝回去
for (int i = begin; i <= end; i++)
{
a[i] = tmp[i];
}
//memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
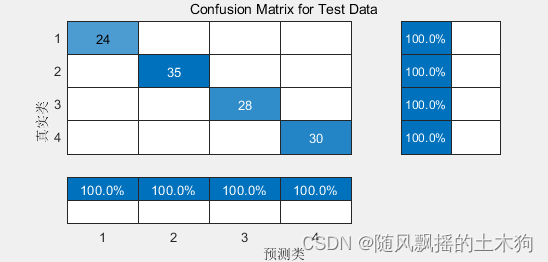
}OK,测试一下:
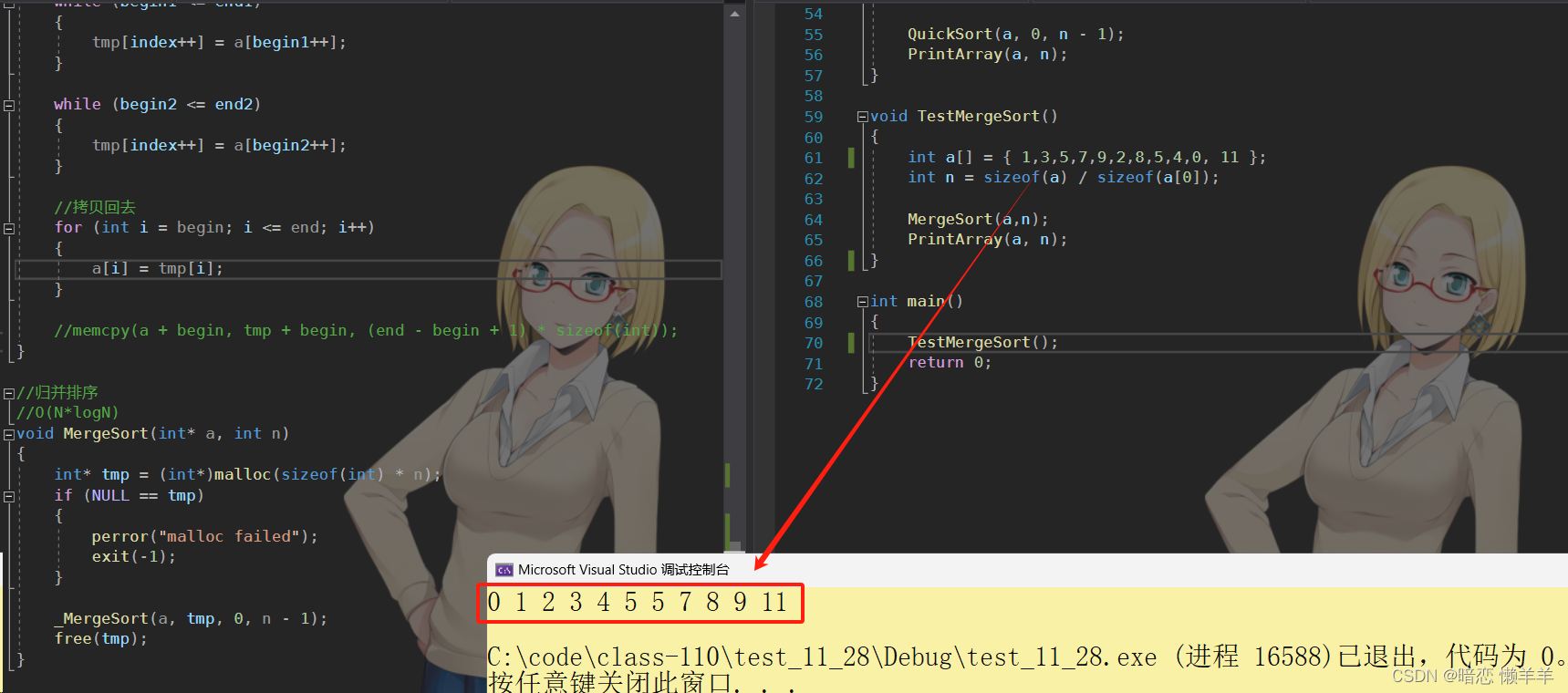
OK,没有问题~!递归版本的是比较简单的,我们下面来实现一下非递归版本的~!
归并排序非递归版
和递归的思路反着来,从下往上一个一个一组归并,一一组归并好了,两两一组往上归并...,直到整个序列有序~!
OK,还是画个图:
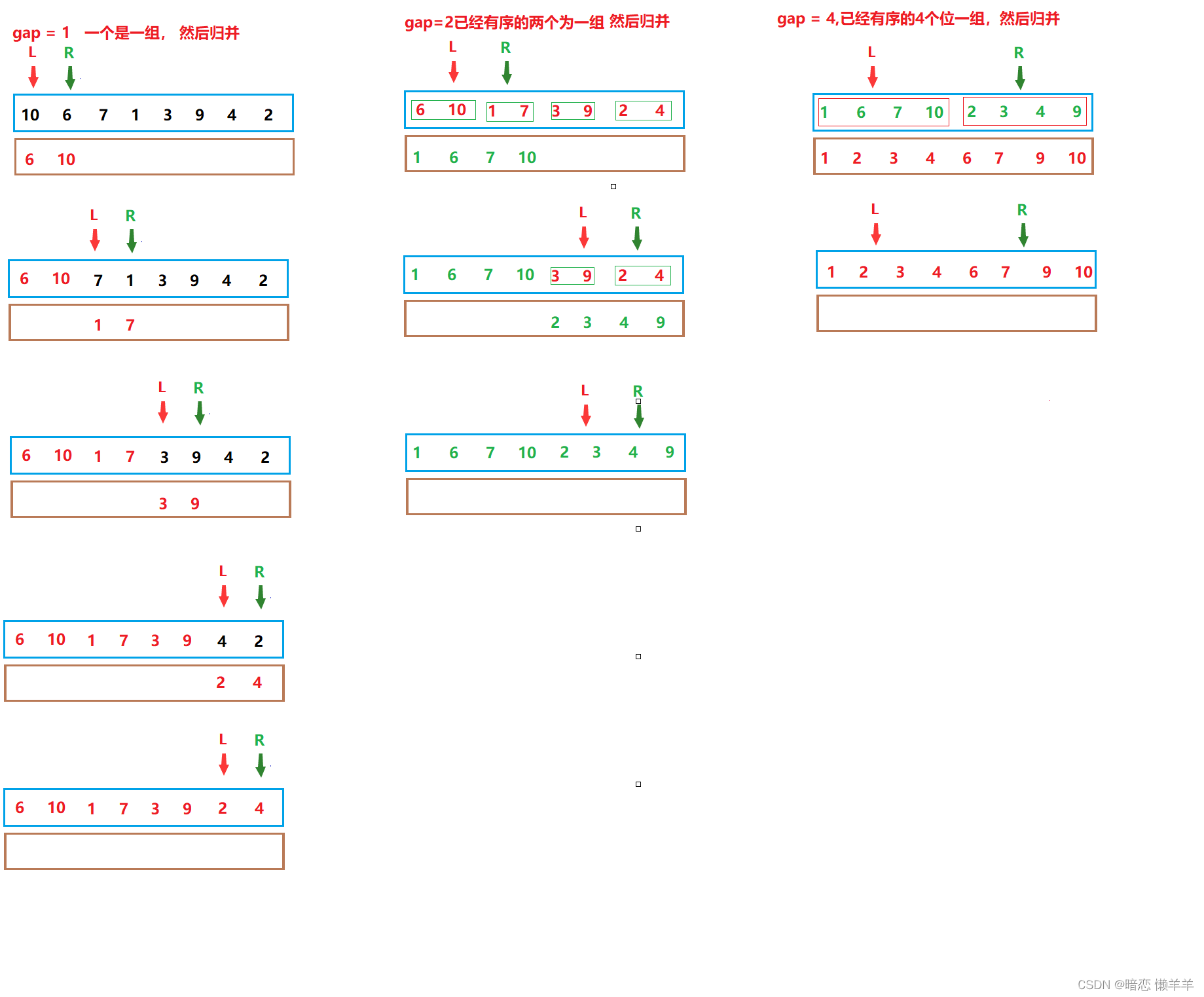
这里的问题就是,如何控制每次归并的子序列的范围?以及什么时候结束归并?
一、gap 控制几个为一组归并(gap一开始从1开始),则:
第一个子序列的起始是begin1 = i, end1 = i + gap -1;
第二个子序列的起始是begin2 = i+gap, end2 = i + 2 *gap - 1;
其中i是遍历一遍待排序的数组的下标,i从0开始。但注意的是,i每次跳几步呢?如下图,i每次应该跳2*gap步。
二、gap控制的是每次几个为一组我们 一开始是1个,2个、4个、8个,显然是2的倍数,所以gap每次乘等2即可!也不能一直让gap*=2下去,gap不可能大于等于数组的长度,所以当超过数组的长度是结束!

还有一个比较坑爹的点就是,数组的长度不一定给是偶数啊,上面介绍的只是因于数组长度是偶数的情况,非偶数的情况gap*=2,后面如果一分为2 的长度不够,就会越界,如下图。
解决方案:判断,当begin2\end2\end1越界时判断一下,当end2越界时,说明前面的区间都存在,只需要end2调整到n-1的位置即可。当begin2\end1越界时说明后面的区间不存在,直接不要排序了,又因为end1越界时begin2必定越界,所以可以直接用begin2来判断也可以~!

OK, 介绍到这里就可以上代码了:
void MergeSortNoR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc failed");
exit(-1);
}
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2*gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
//第二组不存在就不要排了
if (begin2 >= n)//if (end1 >= n ||begin2 >= n)
{
break;
}
//当end2越界时调整到n-1的位置
if (end2 >= n)
{
end2 = n - 1;
}
int index = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
//拷贝回去
//for (int k = i; k <= end2; k++)
//{
// a[k] = tmp[k];
//}
memcpy(a + i, tmp + i, (end2 - i + 1) * sizeof(int));
}
gap *= 2;
}
free(tmp);
}测试一下:
复杂度分析
时间复杂度:O(N*logN)
我们上面说过,他像二叉树的后序遍历,高度是logN,每一层合计归并时O(N)遍历一遍数组
空间复杂度:O(N)
N为辅助数组的长度,和原数组的长度一样!
计数排序
计数排序是一种非比较排序,他又称鸽巢原理或抽屉原理(小学数学)。其实如果你学过哈希表的话,你就知道它实际上是哈希寻址的一种变形而已!(哈希全家桶的那一套会在后面C++介绍和实现)
思路:统计每个元素的出现的次数,根据统计的结果把元素放到原数组中!
什么意思?白话一点说就是,一个元素(也有可能是处理过的元素)作为统计数组的下标,每出现一次都会记录一次。等统计结束后根据每个位置出现的次数依次放回原数组,放的元素就是统计数组的下标(或下标+处理的值)~!
注意这里统计的话要有一个专门的统计数组,数组的大小为最大值-最小值+1(保证所有的数都可以被统计)。
OK,画个图:
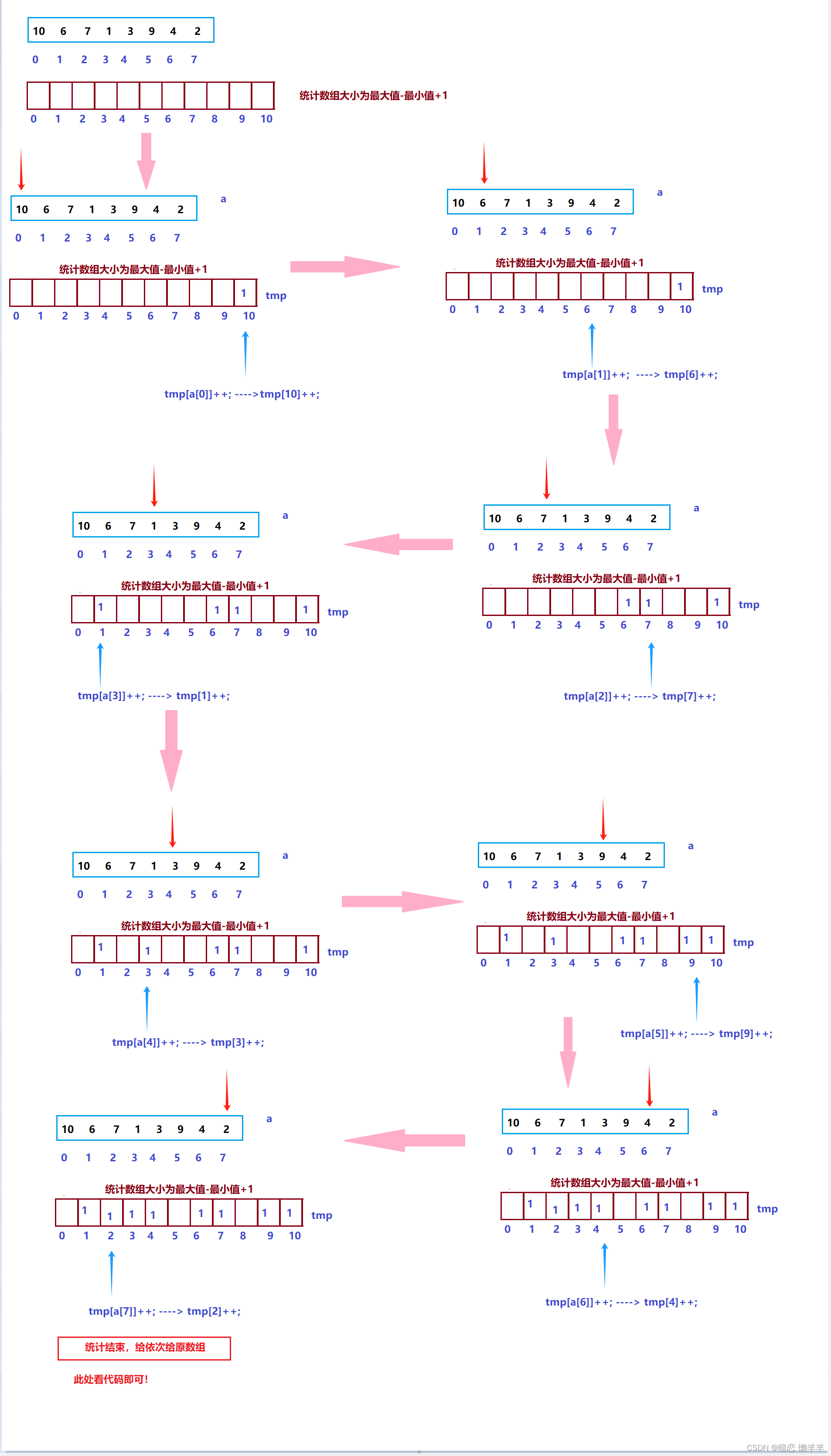
这里还有一个问题就是如果,要排序的数组元素是,100,102,101,111,110,199,188,200
按上述的话,开200个空间,前半部分浪费了。如何将解决呢?其实我们只需要映射一下就OK了,每个元素统计时减去最小值,放回是 每个元素再加上即可~!也就是100是最小的,100-100==0,即100在0号下标的位置++一下即可~!这样旧只需要开max-min +1个空间了,节省了不必要的空间~!
这就是上面说的处理过的元素~!
上代码:
//计数排序
void CountSort(int* a, int n)
{
//找最大和最小的元素
int min = a[0], max = a[0];
for (int i = 0; i < n; i++)
{
if (min > a[i])
min = a[i];
if (max < a[i])
max = a[i];
}
//开max - min + 1 的空间
int* tmp = (int*)calloc((max - min + 1), sizeof(int));
if (NULL == tmp)
{
perror("malloc failed");
exit(-1);
}
//统计出现的次数
for (int i = 0; i < n; i++)
{
tmp[a[i] - min]++;
}
//依次给原数组即可
int index = 0;
for (int i = 0; i < max - min + 1; i++)
{
while (tmp[i]--)
{
a[index++] = i + min;
}
}
}OK,测试一下:

复杂度分析
时间复杂度:O(N+K)
N为原数组的大小, K为统计数组的大小。遍历一遍数组找最大和最小O(N),统计O(N), 拷贝回去O(N+K)遍历一遍统计数组的同时还要遍历一原数组!
空间复杂度:O(K)
K是统计数组的大小~!
注意:计数排序效率还可以,但他的致命缺陷就是比较适合数据相对集中的数字据,如果不集中的话或很浪费空间例如:1,2,5,3,4,0,888,9999,1111,11,7,4这样的数据。
OK~!本期本想就到这里,好兄弟我们下期再见~!