本文内容借鉴一本我非常喜欢的书——《数据结构与算法图解》。学习之余，我决定把这本书精彩的部分摘录出来与大家分享。   

目录

写在前面

1.选择排序

2.选择排序实战

3.选择排序的实现

4.选择排序的效率

5.忽略常数

6.大O的作用

7.总结

---

写在前面

大 O 是一种能够比较算法效率，并告诉我们在特定环境下应采用何种算法的伟大工具。但我们不能完全依赖于它。

因为有时候即使两种算法的大 O 记法完全一样，但实际上其中一个比另一个要快得多。

本章我们就来学习如何分辨那些效率貌似一样的算法，从而选出较快的那个。

---

1.选择排序

上一章分析了冒泡排序算法，其效率是 O(N^2 )。现在我们再来探索另一种排序算法，选择排
序，并将它跟冒泡排序对比一下。

运用大O来给代码提速（冒泡排序）http://t.csdn.cn/PTevF选择排序的步骤如下。

(1) 从左至右检查数组的每个格子，找出值最小的那个。在此过程中，我们会用一个变量来记住检查过的数字的最小值（事实上记住的是索引，但为了看起来方便，下图就直接写出数值）。如果一个格子中的数字比记录的最小值还要小，就把变量改成该格子的索引，如图所示。

(2) 知道哪个格子的值最小之后，将该格与本次检查的起点交换。第 1 次检查的起点是索引 0，
第 2 次是索引 1，以此类推。下图展示的是第一次检查后的交换动作。

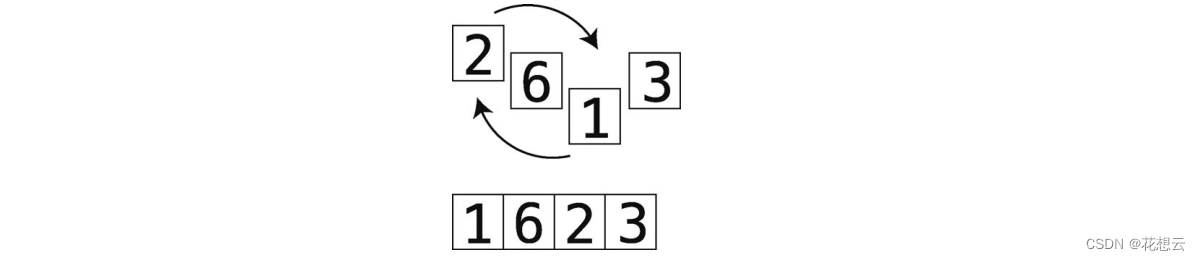
(3) 重复第(1) (2)步，直至数组排好序。 

---

2.选择排序实战

以数组 [4,2,7,1,3] 为例，步骤如下。

开始第 1轮检查。

首先读取索引 0。根据此算法的定义，它是目前遇到的最小值（因为现在只检查了一个格子），于是记下其索引。

第 1步：将索引 1的值 2与目前的最小值 4进行比较。

2比 4还要小，于是将目前的最小值改为 2。

第 2步：再与下一个值做比较。因为 7大于 2，所以最小值还是 2。

第 3步：将 1和目前的最小值做比较。 

1比 2还要小，于是目前的最小值更新为 1。

第 4步：比较 3和目前的最小值 1。因为现在已经走到数组尽头了，所以可以断定 1是整个
数组的最小值。 

第 5步：本次检查的起点是索引 0，不管那里的值是什么，我们都应该将最小值 1换到那里。

现在 1就排到正确的位置上了。

可以开始第 2轮检查了。 

准备工作：因为索引 0的值已符合其排位，所以这一轮从下一个格子开始，即索引 1，其值为 2，也是目前本轮所遇到的最小值。

第 6步：将 7跟目前的最小值 2进行比较。因为 2小于 7，所以最小值仍为 2。

 第 7步：将 4跟目前的最小值 2进行比较。因为 2小于 4，所以最小值仍为 2。

第 8步：将 3跟目前的最小值 2进行比较。因为 2小于 3，所以最小值仍为 2。 

又走到数组尽头了。本轮不需要做任何交换，2已在其正确位置上。于是第 2轮检查结束，现在数组如下图所示。 、

开始第 3轮检查。 

准备工作：从索引 2起，其值为 7。于是本轮目前最小值为 7。

第 9 步：比较 4 与 7。

将 4 记为目前的最小值。 

第 10 步：遇到 3，它比 4 还小。

于是 3 成了目前的最小值。

第 11 步：到数组尽头了，将 3 跟本轮起点 7 进行交换。 

于是 3 排到正确位置上了。 

虽然我们可以看到现在整个数组都有序了，但计算机是看不到的，它只会继续第 4轮检查。

准备工作：此轮检查从索引 3开始，其值 4是目前的最小值。

第 12步：比较 4和 7。 

4仍为最小值，而且它也处于本轮起点，因此无须任何交换。

因为最后一个格子左侧的那些值都已在各自的正确位置上，所以最后一格也必然正确，于是排序结束。

---

3.选择排序的实现

下面是用C语言实现的选择排序：

void SelectSort(int arr[], int n)//升序
{
	for (int i = 0; i < n-1; i++) //n个数，只需排好n-1个，剩下的一个自然在正确的位置上
	{
		int min = i;      //用min来记录最小值的索引（下标）         
		
        for (int j = i+1; j < n; j++)  //从i索引的后一个开始比较
		{
			if (arr[j] < arr[min])
			{
				min = j;            //找到比自己小的数的索引，并成为它
			}
		}
		if (min != i)               //如果min的值改变，则与i处的值交换
		{
			int tmp = arr[i];
			arr[i] = arr[min];
			arr[min] = tmp;
		}
	}
}

下面来进行分析：

for (int i = 0; i < n-1; i++) 

这个外层的循环代表每一轮检查。在一轮检查之初，我们会先记住目前的最小值的索引。

int min = i;

因此每轮开始时 min 都会是该轮的起点索引 i 。

注意我们实际上记录的是最小值的索引，而非最小值本身。于是，第 1 轮开始时最小值的索引是 0，到第 2 轮则是 1，以此类推。

for (int j = i+1; j < n; j++)

这个内层循环控制的是找出最小值的索引的过程。

if (arr[j] < arr[min])
{
	min = j;            
}

循环内逐个检查数组未排序的格子，若遇到比之前记录的本轮最小值还小的格子值，就将min更新为该格子的索引。

内层循环结束时，会得到未排序数值中最小值的索引。

if (min != i)
{
	int tmp = arr[i];
	arr[i] = arr[min];
	arr[min] = tmp;
}

然后再看看这个最小值是否已在正确位置，即该索引是否等于 i 。如果不是，就将 i 所指的值与最小值交换。

---

4.选择排序的效率

选择排序的步骤可分为两类：比较和交换。

若有 N个元素，就会有 (N - 1) + (N - 2) + (N - 3) + … + 1次比较。

但每轮的交换最多只有 1 次。如果该轮的最小值已在正确位置，就无须交换，否则要做 1 次交换。相比之下，冒泡排序在最坏情况（完全逆序）时，每次比较过后都要进行 1 次交换。

下表为冒泡排序和选择排序的并列对比。

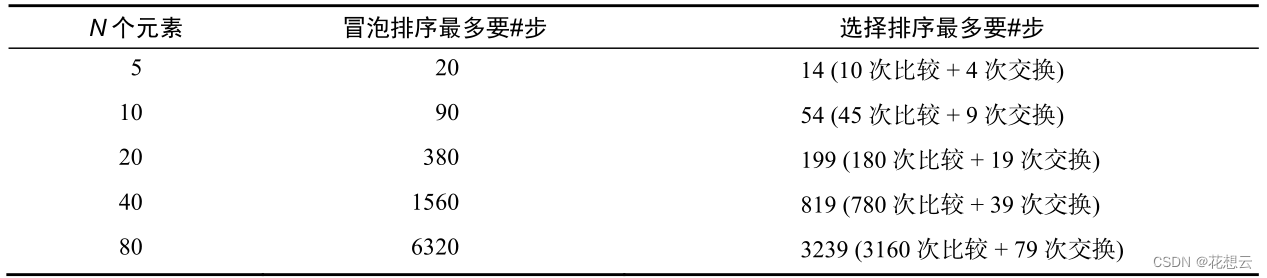
从表中可以清晰地看到，选择排序的步数大概只有冒泡排序的一半，即选择排序比冒泡排序快一倍。 

---

5.忽略常数

但有趣的是，选择排序的大 O记法跟冒泡排序是一样的。

还记得我们说过，大 O记法用来表示步数与数据量的关系。所以你可能会以为步数约为 N^2的一半的选择排序，其大 O会写成 O(N ^2/ 2)，以表示 N个元素需要 N ^2 / 2步。如下表所示。

但事实上，选择排序的大 O记法为 O(N^2 )，跟冒泡排序一样。这是因为大 O记法的一条重要
规则：

大 O 记法忽略常数。

---

6.大O的作用

尽管不能比较冒泡排序和选择排序，大 O 还是很重要的，因为它能够区分不同算法的长期增长率。当数据量达到一定程度时，O(N)的算法就会永远快过 O(N^2 )，无论这个 O(N)实际上是O(2N)还是 O(100N)。

下图为 O(N)和 O(N^2 )的对比。

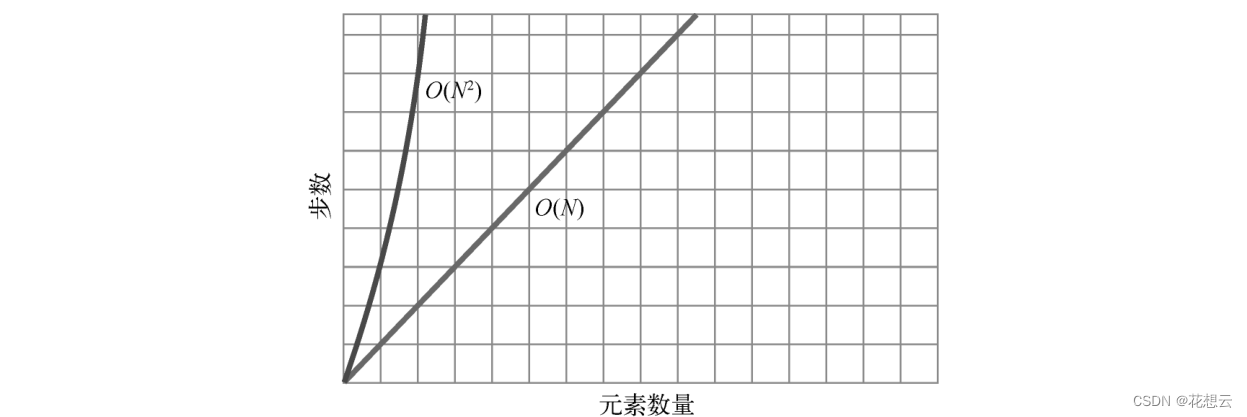
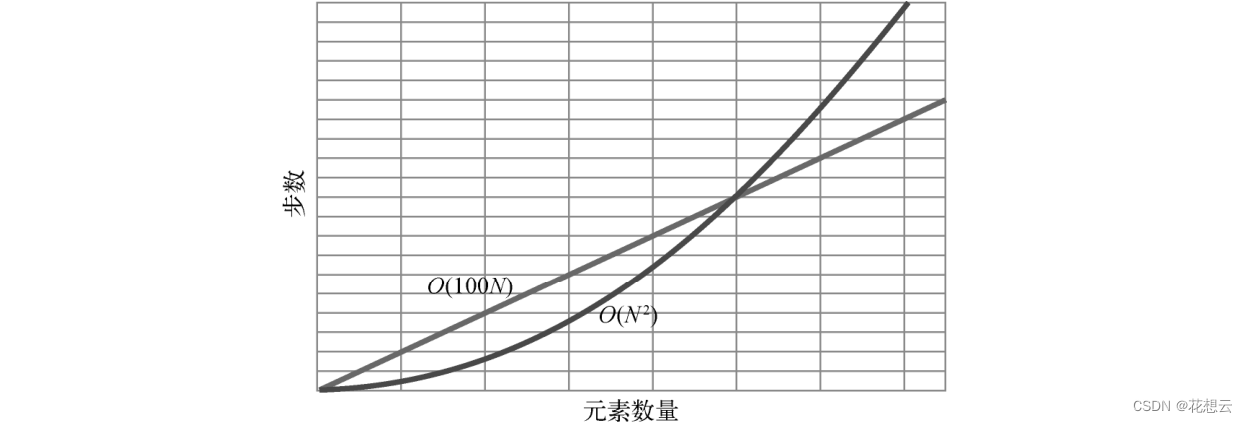
这就是大 O 记法忽略常数的原因。大 O 记法只表明，对于不同分类，存在一临界点，在这一点之后，一类算法会快于另一类，并永远保持下去。至于这个点在哪里，大 O并不关心。

因此，不需要写成 O(100N)，归类到 O(N)就好了。

---

7.总结

现在我们已经掌握了一些非常强大的算法分析手法。我们能够使用大 O去判断各种算法的效率，即便两种算法的大 O记法一样，也知道如何对比它们。不过在对比算法时，还需要考虑一个重要因素。至今我们关注的都是最坏情况下算法会跑得多慢，但其实最坏情况并不总会发生。没错，我们遇到的大都是平均情况。下一章，我们会学习怎样顾及所有情况。