一、题目描述

二、思路分析

这道题中，其实刚一看是非常的抽象的，也是非常麻烦的。麻烦的点在于我们既需要考虑横着放的方块，又需要考虑竖着放的方块。

但是我们注意到，只要我们放好横着放的方块，竖着的方块的放法是唯一确定的，因此我们只需要考虑横放的方块。

这道题我们采用动态规划的方式来做，而动规的核心思路就是枚举子问题，利用子问题来解决当前的问题，那么这道题的子问题是什么呢？

我们不动行数，让列数从小到大增大，列数较小的看作子问题。

然后我们如何拜访横着的方块呢？

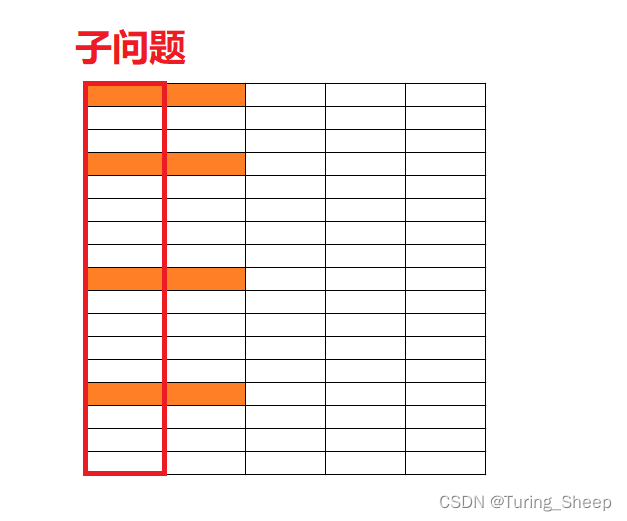
我们方块的摆放上图的方式，即，当前列的某几行的方块延申到了下一列。

那么我们如果两列一起看是不是就相当于在某几行放了一个方块。

但是并不是所有的方案都是合法的，比如下面这几种方法就是不合理的：

情况1：

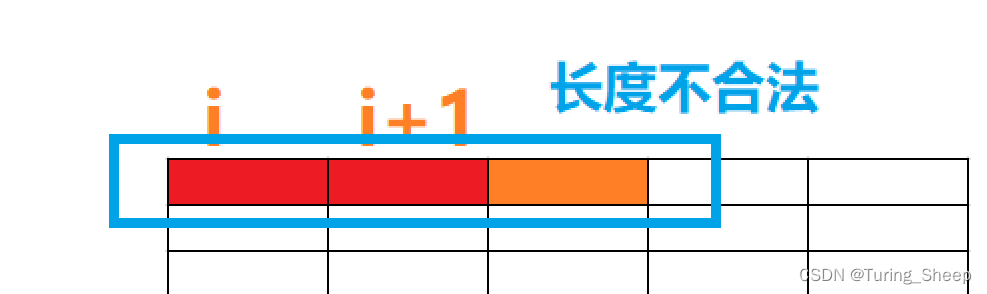
在第i列的时候，我们让第一行延申，在第i+1列的时候，还让i+1延申，那么很显然最终构成的长方体是3*1，不合法。

情况2：

两个延申行中间的间隔是奇数，导致我们无法利用竖着的填充满。

1、状态表示——状态压缩

问题的关键是如何表示，某列是否延申，这里就要用到今天的重点，状态压缩 。即将一种状态压缩成二进制数。 什么意思呢？

我们规定：1代表延申，0代表不延申。

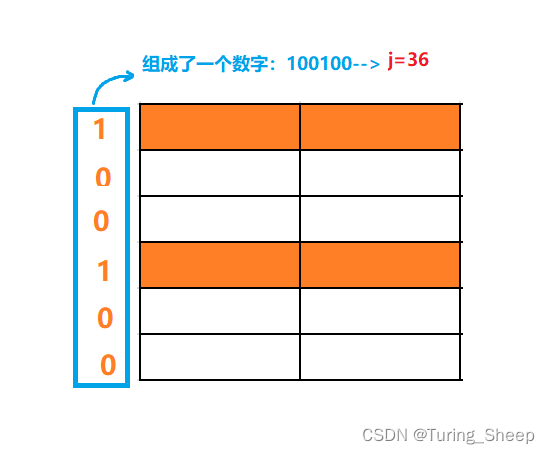
如上图所示，我们将上图中的一种状态压缩成了一个数字 j。所以$j$就表示我们表格中的延申状态。

因此假设行数是$5$行，我们只需要从$00000$到$11111$去枚举每一种状态，然后我们判断是否合法即可。

而中间的状态枚举，即写一个循环$0$到$2^5-1$

所以状态表示：

$f[i][j]$：共i列，且第i列向下一行延申的状态是j的所有方案数。

最终状态：

假设表格有k列，那么最终表示就是$f[k][0]$，意思就是第k列不延申到下一列。

2、状态转移

假设我们下面的列数均合法，则：
$$f(i,j)=sum(f(i-1,k))(j\&k=0，j|k是合法状态)$$

3、循环

外循环就是我们的列数，内循环就是我们每一列可能的延申情况。

4、初始化

第0列中延申0个，这种情况下，f[0][0]=1

三、代码

#include<iostream>
#include<cstring>
using namespace std;
const int N=15,M=1<<N;
long long dp[N][M];
bool st[M];
int n,m;
int main()
{
    while(cin>>n>>m,n||m)
    {
        for(int i=0;i<1<<n;i++)
        {
            int cnt=0;
            st[i]=true;
            for(int j=0;j<n;j++)
            {
                if((i>>j)&1)
                {
                    if(cnt&1)
                    {
                        st[i]=false;
                        break;
                    }
                }
                else cnt++;
            }
            if(cnt&1)st[i]=false;
        }
        memset(dp,0,sizeof dp);
        dp[0][0]=1;
        for(int i=1;i<=m;i++)
        {
            for(int j=0;j<1<<n;j++)
            {
                for(int k=0;k<1<<n;k++)
                {
                    if(!(j&k)&&st[j|k])dp[i][j]+=dp[i-1][k];
                }
            }
        }
        cout<<dp[m][0]<<endl;
    }
    return 0;
}