数组是存储在连续内存空间上的相同类型数据的集合。在数组中可以方便地通过下标索引的方式获取对应的数据。
需要注意的是：

• 数组的下标都是从0开始的。
• 数组在内存空间是连续的，所以删除或者增添元素时难免要移动其他元素的地址，只能覆盖。

leedcode26：删除有序数组中的重复项
给你一个 升序排列 的数组 nums ，请你 原地 删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。元素的 相对顺序 应该保持一致 。
不要使用额外的数组空间，你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
示例：

输入：nums = [1,1,1,2,2,3]
输出：5, nums = [1,1,2,2,3]
解释：函数应返回新长度 length = 5, 并且原数组的前五个元素被修改为 1, 1, 2, 2, 3 。 不需要考虑数组中超出新长度后面的元素。

方法：使用双指针
算法思路：
数组完成排序后，我们可以放置两个指针i和j，其中i是慢指针，j是快指针。只要nums[i]=nums[j]，我们就加一移动j的位置，以跳过重复项。
当遇到nums[i]!=nums[j]时，我们就需要把nums[j]的值复制给nums[i+1]，然后接着重复循环，直到j指针到达数组的末尾为止。
代码如下：

class Solution {
    public int removeDuplicates(int[] nums) {
         //双指针法，i慢指针，j块指针
         if(nums.length==0){
             return 0;
         }
         int i=0;
         for(int j=1;j<nums.length;j++){
             if(nums[i]!=nums[j]){
                 i++;
                 nums[i]=nums[j];
             }
         }
         return i+1;
    }
}

leedcode724：寻找数组的中心下标
给你一个整数数组 nums ，请计算数组的 中心下标 。
数组 中心下标 是数组的一个下标，其左侧所有元素相加的和等于右侧所有元素相加的和。
如果中心下标位于数组最左端，那么左侧数之和视为 0 ，因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。
如果数组有多个中心下标，应该返回 最靠近左边 的那一个。如果数组不存在中心下标，返回 -1 。
示例1：

输入：nums = [1, 7, 3, 6, 5, 6]
输出：3
解释：
中心下标是 3 。
左侧数之和 sum = nums[0] + nums[1] + nums[2] = 1 + 7 + 3 = 11 ，
右侧数之和 sum = nums[4] + nums[5] = 5 + 6 = 11 ，二者相等。

示例2：

输入：nums = [1, 2, 3]
输出：-1
解释：
数组中不存在满足此条件的中心下标。

示例3：

输入：nums = [2, 1, -1]
输出：0
解释：
中心下标是 0 。
左侧数之和 sum = 0 ，（下标 0 左侧不存在元素），
右侧数之和 sum = nums[1] + nums[2] = 1 + -1 = 0

方法：使用前缀和
算法思路：先统计出整个数组的总和，然后从第一个元素开始叠加，总和递减当前元素，叠加递增当前元素，直到两个值相等，此时叠加元素的下标就是中心下标。

代码如下：

class Solution {
    //使用前缀和的方法
    public int pivotIndex(int[] nums) {
        //sum_right代表总的大小
        int sum_right=Arrays.stream(nums).sum(); 
        int sum_left=0;
        for(int i=0;i<nums.length;i++){
        //加上当前数组元素值
         sum_left=sum_left+nums[i];
         if(sum_left==sum_right){
             return i;//返回中心下标
         }
         //向右移动减去当前的数组元素值
         sum_right=sum_right-nums[i];
        }
        return -1;
    }
}

leedcode 27. 移除元素
给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。
不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
示例：

输入：nums = [3,2,2,3], val = 3
输出：2, nums = [2,2] 解释：函数应该返回新的长度 2, 并且nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如，函数返回的新长度为 2 ，而 nums =2,2,3,3] 或 nums = [2,2,0,0]，也会被视作正确答案。

方法一、暴力解法

class Solution {
    //暴力解法
    public int removeElement(int[] nums, int val) {
     int size=nums.length;
     for(int i=0;i<size;i++){
          if(nums[i]==val){
            //如果发现需要移除的元素就将数组整体向前移动一位
            for(int j=i+1;j<size;j++){
                nums[j-1]=nums[j];
            }
          //因为数组整体向前移动一位，所以i的下标也应向前移动一位。因为下一次i也是原来的位置所以需要--
          i--;
          size--;//此时数组长度减一
          }

     }
     return size;
    }
}

方法二、双指针

class Solution {
    public int removeElement(int[] nums, int val) {
    //slow慢指针，fast块指针
      int slow=0;
      for(int fast=0;fast<nums.length;fast++){
          if(nums[fast]!=val){
              nums[slow]=nums[fast];
              slow++;
          }
      }
      return slow;
    }
}

leedcode 209. 长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。
示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

方法一、暴力解法

class Solution {
    //暴力解法
    public int minSubArrayLen(int target, int[] nums) {
      int result=Integer.MAX_VALUE;//最终结果
      int sum=0;//子数组的元素之和
      int subLength=0;//子数组的长度
      
      for(int i=0;i<nums.length;i++){ //设置子数组的起点位置是i
          sum=0;
          for(int j=i;j<nums.length;j++){//设置子数组的终止位置是j
            sum=sum+nums[j];
            if(sum>=target){//进行记录,更新result
              subLength=j-i+1;//获取子数组长度
              result=result<subLength?result:subLength;//获取长度最小的结果
              break;
            }
          }
      }
      return result==Integer.MAX_VALUE?0:result;

    }
}

方法二、滑动窗口

class Solution {
    //滑动窗口，双指针的一种
    public int minSubArrayLen(int target, int[] nums) {
      
      int sum=0;//记录总和
      //起始位置
      int i=0;
      int sublength=0;//记录长度
      int result=Integer.MAX_VALUE;
      for(int j=0;j<nums.length;j++){
          sum=sum+nums[j];
          //滑动窗口
          while(sum>=target){
            sublength=j-i+1;//获取子数组的长度
            result=Math.min(sublength,result);//取得长度最小的子数组
            //不断变更i（子数组的起始位置）
            sum=sum-nums[i];
            i++;
          }
      }
      //如果result没有赋值，则返回0，说明没有符合
      return result==Integer.MAX_VALUE?0:result;
    }
}

leedcode59. 螺旋矩阵 II
给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

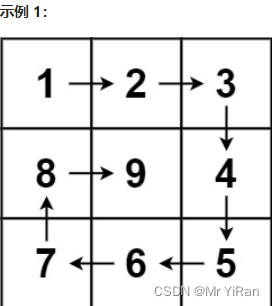
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

整体代码如下：

class Solution {
    //循环不变量，按照左闭右开的原则
    public int[][] generateMatrix(int n) {
      
      int start=0;//定义每次循环的开始点
      int loop=0;//控制循环次数
      int [][] res=new int[n][n];
      int count=1;//定义填充的数字
      int i,j;//i表示纵坐标，j为横坐标
      while(loop++ <n/2){//n/2表示转几圈

          //模拟上侧从左到右
          for(j=start;j<n-loop;j++){
              res[start][j]=count++;
          }

          //模拟右侧从上到下
          for(i=start;i<n-loop;i++){
              res[i][j]=count++;
          }

          //模拟下侧从右到左
          for(;j>=loop;j--){
              res[i][j]=count++;
          }

          //模拟左侧从下到上
          for(;i>=loop;i--){
              res[i][j]=count++;
          }
          //下一圈的时候start要加一，表示下一卷的起始
          start++;
      }
      //当转的圈数是奇数时，则需要单独给矩阵最中间的位置赋值
      if(n%2==1){
          res[start][start]=count;
      }
      return res;
    }
}