论文地址:https://arxiv.org/pdf/1707.06347.pdf
一、 置信域方法(Trust Region Methods)
设
π
θ
o
l
d
\pi_{\theta_{old}}
πθold是先前参数为
θ
o
l
d
\theta_{old}
θold的策略网络,
π
θ
\pi_{\theta}
πθ则是当前待优化的策略网络,则TRPO的优化目标是:
maximize
θ
E
^
t
[
π
θ
(
a
t
∣
s
t
)
π
θ
o
l
d
(
a
t
∣
s
t
)
A
^
t
]
subject
to
E
^
t
[
KL
[
π
θ
o
l
d
(
⋅
∣
s
t
)
,
π
θ
(
⋅
∣
s
t
)
]
]
≤
δ
\begin{align} &\mathop{\text{maximize}}_{\theta}\quad\hat{\mathbb{E}}_t\Big[\frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}\hat{A}_t \Big] \\ &\mathop{\text{subject}\;\text{to}}\quad\hat{\mathbb{E}}_t[\text{KL}[\pi_{\theta_{old}}(\cdot|s_t),\pi_{\theta}(\cdot|s_t)]]\leq\delta \end{align}
maximizeθE^t[πθold(at∣st)πθ(at∣st)A^t]subjecttoE^t[KL[πθold(⋅∣st),πθ(⋅∣st)]]≤δ
其中,
A
^
t
\hat{A}_t
A^t是
t
t
t时刻的优势函数估计值。
r
t
(
θ
)
=
π
θ
(
a
t
∣
s
t
)
π
θ
o
l
d
(
a
t
∣
s
t
)
r_t(\theta)=\frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}
rt(θ)=πθold(at∣st)πθ(at∣st)是用来控制新旧策略的差异,若差异到则会增加更新幅度,反之则降低更新幅度。约束条件则是新旧策略函数的KL散度,该约束会控制新旧策略的差距不会太大。但是,求解这个带约束的优化问题实现复杂且计算量大。
理论上证明TRPO在实践中,建议使用惩罚项而不是约束,即转换为无约束优化问题。
maximize
θ
E
^
t
[
π
θ
(
a
t
∣
s
t
)
π
θ
o
l
d
(
a
t
∣
s
t
)
A
^
t
−
β
KL
[
π
θ
o
l
d
(
⋅
∣
s
t
)
,
π
θ
(
⋅
∣
s
t
)
]
]
\mathop{\text{maximize}}_{\theta}\quad\hat{\mathbb{E}}_t\Big[\frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}\hat{A}_t-\beta\text{KL}[\pi_{\theta_{old}}(\cdot|s_t),\pi_{\theta}(\cdot|s_t)]\Big]
maximizeθE^t[πθold(at∣st)πθ(at∣st)A^t−βKL[πθold(⋅∣st),πθ(⋅∣st)]]
其中,
β
\beta
β是超参数。TRPO使用硬约束而不是惩罚项,是因为很难选择单个
β
\beta
β在所有不同问题上均表现良好。实验也表明,简单选择固定的惩罚系数
β
\beta
β并用SGD优化惩罚目标是不够的,需要额外的修改。
二、Clipped Surrogate Objective
由于
r
t
(
θ
)
=
π
θ
(
a
t
∣
s
t
)
π
θ
o
l
d
(
a
t
∣
s
t
)
r_t(\theta)=\frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}
rt(θ)=πθold(at∣st)πθ(at∣st),显然
r
t
(
θ
o
l
d
)
=
1
r_t(\theta_{old})=1
rt(θold)=1。TRPO最大化”代理“目标函数:
L
CPI
(
θ
)
=
E
^
t
[
π
θ
(
a
t
∣
s
t
)
π
θ
o
l
d
(
a
t
∣
s
t
)
A
^
t
]
=
E
^
t
[
r
t
(
θ
)
A
^
t
]
L^{\text{CPI}}(\theta)=\hat{\mathbb{E}}_t\Big[\frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}\hat{A}_t\Big]=\hat{\mathbb{E}}_t[r_t(\theta)\hat{A}_t]
LCPI(θ)=E^t[πθold(at∣st)πθ(at∣st)A^t]=E^t[rt(θ)A^t]
在没有约束的情况下,最大化
L
CPI
L^{\text{CPI}}
LCPI有可能会大幅度更新策略;因此,需要修改目标函数来惩罚
r
t
(
θ
)
r_t(\theta)
rt(θ)远离1。
因此提出目标函数
L
CLIP
(
θ
)
=
E
^
t
[
min
(
r
t
(
θ
)
A
^
t
,
clip
(
r
t
(
θ
)
,
1
−
ϵ
,
1
+
ϵ
)
A
^
t
]
L^{\text{CLIP}}(\theta)=\hat{\mathbb{E}}_t\Big[\min(r_t(\theta)\hat{A}_t,\text{clip}(r_t(\theta),1-\epsilon,1+\epsilon)\hat{A}_t\Big]
LCLIP(θ)=E^t[min(rt(θ)A^t,clip(rt(θ),1−ϵ,1+ϵ)A^t]
ϵ
\epsilon
ϵ截断超参数,通常设置为0.2。
clip()
\text{clip()}
clip()代表截断函数,负责将
r
t
r_t
rt限制在
[
1
−
ϵ
,
1
+
ϵ
]
[1-\epsilon,1+\epsilon]
[1−ϵ,1+ϵ],以保证收敛性。最后,使用无截断和截断目标函数的最小值,从而形成未截断目标函数的下界。
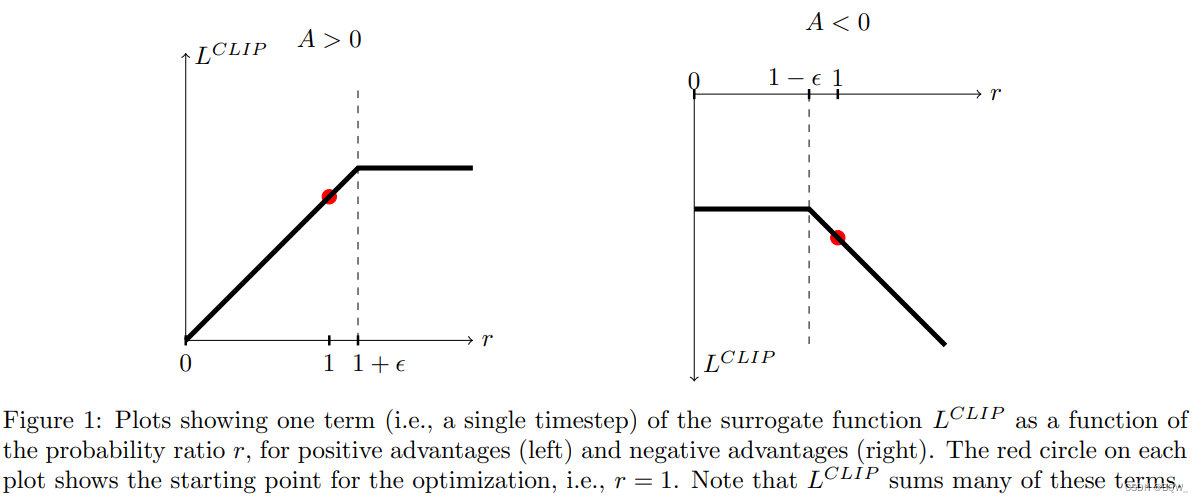
优势函数A可以分为正负两种情况。若优势函数为正,当
r
t
>
1
+
ϵ
r_t>1+\epsilon
rt>1+ϵ时,将不提供额外的奖励;若优势函数为负,当
r
t
<
1
−
ϵ
r_t<1-\epsilon
rt<1−ϵ时,同样不提供额外的奖励,这样就能限制新旧策略的差异。
三、自适应KL惩罚系数
另一种代替或者补充clipped surrogate objective的方案是使用KL散度惩罚,并调整惩罚系数,每次策略更新时使得KL散度 d targ d_{\text{targ}} dtarg达到某个目标值。在作者的实验中,KL惩罚的表现要差于clipped surrogate objective,但其可以作为重要的baseline。
在每次策略更新中执行下面的步骤:
-
利用若干个minibatch SGD的epochs,优化KL惩罚目标
L KLPEN ( θ ) = E ^ t [ π θ ( a t ∣ s t ) π θ o l d ( a t ∣ s t ) A ^ t − β KL [ π θ o l d ( ⋅ ∣ s t ) , π θ ( ⋅ ∣ s t ) ] ] L^{\text{KLPEN}}(\theta)=\hat{\mathbb{E}}_t\Big[\frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}\hat{A}_t-\beta\text{KL}[\pi_{\theta_{old}}(\cdot|s_t),\pi_{\theta}(\cdot|s_t)]\Big] LKLPEN(θ)=E^t[πθold(at∣st)πθ(at∣st)A^t−βKL[πθold(⋅∣st),πθ(⋅∣st)]] -
计算 d = E ^ t [ KL [ π θ o l d ( ⋅ ∣ s t ) , π θ ( ⋅ ∣ s t ) ] ] d=\hat{\mathbb{E}}_t[\text{KL}[\pi_{\theta_{old}}(\cdot|s_t),\pi_{\theta}(\cdot|s_t)]] d=E^t[KL[πθold(⋅∣st),πθ(⋅∣st)]]
若 d < d targ / 1.5 , β ← β / 2 d<d_{\text{targ}}/1.5,\beta\leftarrow\beta/2 d<dtarg/1.5,β←β/2
若 d > d targ × 1.5 , β ← β × 2 d>d_{\text{targ}}\times1.5,\beta\leftarrow\beta\times 2 d>dtarg×1.5,β←β×2
更新后的 β \beta β用于下一次的策略更新。
四、完整算法

前面推导的surrogate损失函数能够在典型的策略梯度上简单改动即可实现。大多数的优势函数都使用一个可学习的状态价值函数
V
(
s
)
V(s)
V(s)。若策略网络和价值网络共享神经网络架构,那么需要使用一个结合了策略函数和值函数误差项的损失函数。目标函数可以进一步添加熵正则来确保充分的探索。合并这些项,就能够获得下面的目标函数:
L
CLIP+VF+S
(
θ
)
=
E
^
t
[
L
t
CLIP
(
θ
)
−
c
1
L
t
VF
(
θ
)
+
c
2
S
[
π
θ
]
(
s
t
)
]
L^{\text{CLIP+VF+S}}(\theta)=\hat{\mathbb{E}}_t[L_t^{\text{CLIP}}(\theta)-c_1L_t^{\text{VF}}(\theta)+c_2S[\pi_{\theta}](s_t)]
LCLIP+VF+S(θ)=E^t[LtCLIP(θ)−c1LtVF(θ)+c2S[πθ](st)]
其中,
c
1
c_1
c1和
c
2
c_2
c2是控制各个项比例的超参数,
S
S
S是熵正则项,
L
t
SF
L^{\text{SF}}_t
LtSF是均方误差损失
(
V
θ
(
s
t
)
−
V
t
targ
)
2
(V_{\theta}(s_t)-V_t^{\text{targ}})^2
(Vθ(st)−Vttarg)2。