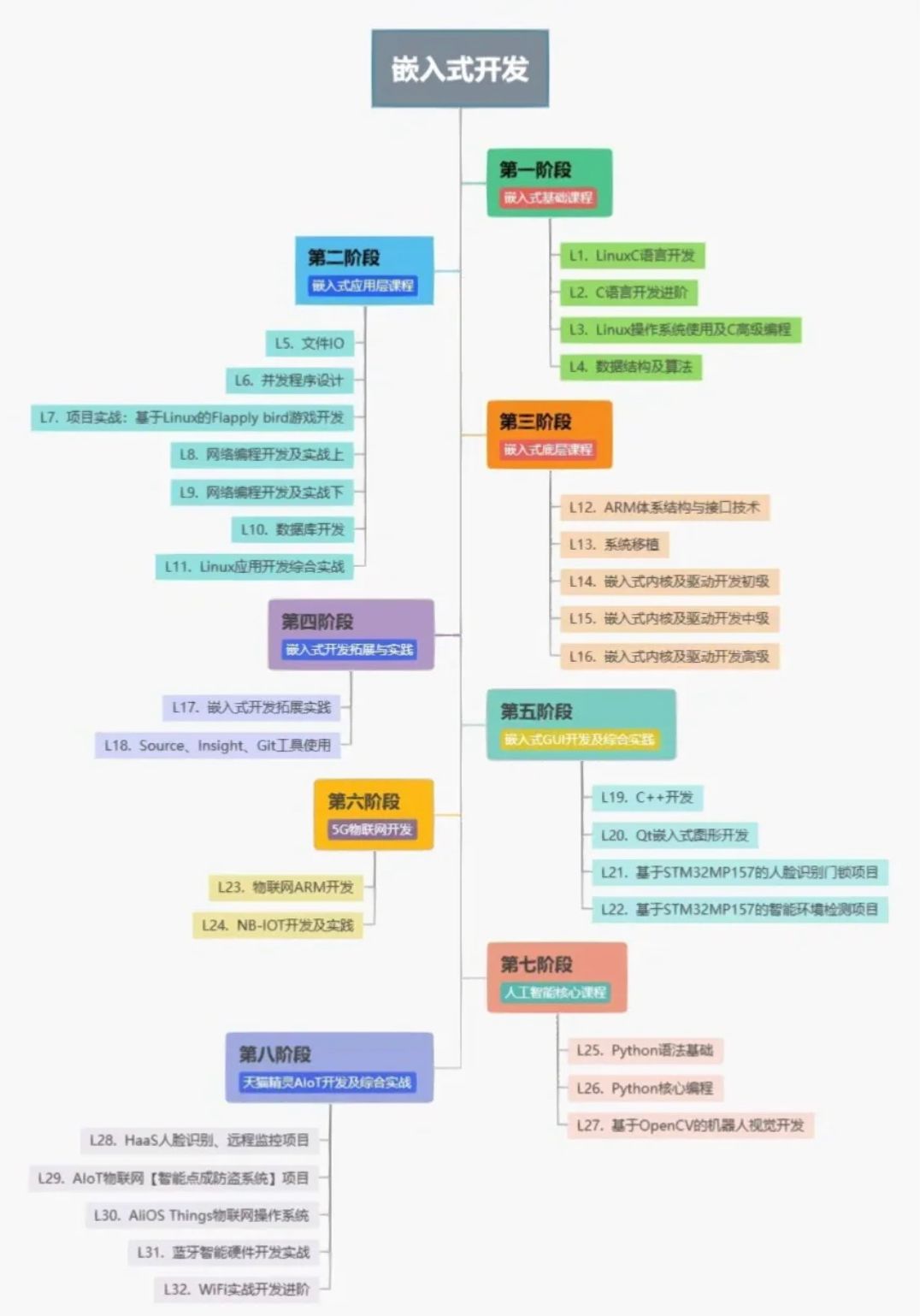
嵌入式开发必须学习qt吗?
在开始前我有一些资料,是我根据自己从业十年经验,熬夜搞了几个通宵,精心整理了一份「 嵌入式的资料从专业入门到高级教程+工具包」,点个关注,全部无偿共享给大家!!!
在评论区回复“888”之后私信回复“888”,即可拿走。在嵌入式开发领域,QT 不是必需的,但学习 QT 会对嵌入式开发者的技能提升有很大帮助。
QT 是一个强大的跨平台 GUI 库,可以帮助开发者快速构建具有图形用户界面的应用程序。在嵌入式开发中,图形用户界面通常是必要的,因此学习 QT 可以使开发者更轻松地创建这些界面。此外,QT 还可以用于创建网络应用程序和嵌入式设备的应用程序,这些也是嵌入式开发中常见的需求。
然而,嵌入式开发并不仅仅涉及 GUI 开发。例如,嵌入式硬件开发、底层驱动开发等也是嵌入式开发的重要部分,这些工作通常不需要学习 QT。
如果你从事嵌入式开发,并希望构建具有图形用户界面的应用程序,那么学习 QT 是非常有益的。但如果你的工作重点在于嵌入式硬件或底层驱动开发,那么学习 QT 可能不是必需的。