一、力扣第144题：二叉树的前序遍历

题目链接：144. 二叉树的前序遍历 - 力扣（Leetcode）

题目描述：

1.解题思路

这道题，在经历了我们上节的分析之后其实难度不大，我们首先遇到的一个困难就是，这个题目要求是传一个数组回去，所以我们必须使用malloc出来的数组，但是这时候产生了第一个困难，数组该开辟多大呢？为了知道开辟多大的数组，我们就得需要先计算出这棵树又多少个结点，于是，我们得先写一个函数去计算结点的个数。计算完毕之后，我们开辟好数组的同时，也将returnSize给他赋值完成。

这样的话，接下来我们就该去遍历这个二叉树，但是二叉树的遍历需要使用递归，而我们肯定不可能递归这个函数，因为这个函数每次都会malloc，所以我们就需要将前序遍历给独立出来，封装成一个函数。这样的话，我们就需要注意的一点就是，当前的数组遍历到哪里去了，这里我们最好使用传址调用。这就是本道题的注意事项了

2.解题代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int TreeSize(struct TreeNode* root)
{
    if(root==NULL)
    {
        return 0;
    }
    else
    {
        return 1+TreeSize(root->left)+TreeSize(root->right);
    }
} 
void _prevOrder(struct TreeNode* root,int* arr,int* i)
{
    if(root==NULL)
    {
        return;
    }
    arr[*i]=root->val;
    (*i)++;
    _prevOrder(root->left,arr,i);
    _prevOrder(root->right,arr,i);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize){
    int size=TreeSize(root);
    int* arr=(int*)malloc(sizeof(struct TreeNode)*size);
    *returnSize=size;
    int i=0;
    _prevOrder(root,arr,&i);
    return arr;
}

二、力扣第94题：二叉树的中序遍历

题目链接：力扣

题目描述：

这道题其实和上一道题基本一致：那么解题思路也不再赘述，这里直接给出代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int TreeSize(struct TreeNode* root)
{
    if(root==NULL)
    {
        return 0;
    }
    return 1+TreeSize(root->left)+TreeSize(root->right);
}
void _InOrder(struct TreeNode* root,int* arr,int* i)
{
    if(root==NULL)
    {
        return ;
    }
    _InOrder(root->left,arr,i);
    arr[*i]=root->val;
    (*i)++;
    _InOrder(root->right,arr,i);
}
int* inorderTraversal(struct TreeNode* root, int* returnSize){
    int size=TreeSize(root);
    int* arr=(int*)malloc(sizeof(struct TreeNode)*size);
    *returnSize=size;
    int i=0;
    _InOrder(root,arr,&i);
    return arr;
}

三、力扣第145题：二叉树的后序遍历

题目链接：力扣

题目描述：

同样的，也与前面的题换汤不换药，这里直接给出代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
 int TreeSize(struct TreeNode* root)
{
    if(root==NULL)
    {
        return 0;
    }
    else
    {
        return 1+TreeSize(root->left)+TreeSize(root->right);
    }
} 
void _PostOrder(struct TreeNode* root,int* arr,int* i)
{
    if(root==NULL)
    {
        return;
    }
    _PostOrder(root->left,arr,i);
    _PostOrder(root->right,arr,i);
    arr[*i]=root->val;
    (*i)++;
}
int* postorderTraversal(struct TreeNode* root, int* returnSize){
    int size=TreeSize(root);
    int* arr=(int*)malloc(sizeof(struct TreeNode)*size);
    *returnSize=size;
    int i=0;
    _PostOrder(root,arr,&i);
    return arr;
}

四、力扣第104题：二叉树的最大深度

题目链接：力扣

题目描述：

1.解题思路

对于这道题，我们的思想还是使用分治算法，分而治之。也就是需要使用递归，我们是这样想的，当我们接受一棵树以后，我们先判断这颗树是不是为空，为空的话，那么他的高度或深度当然就是0了，但是不为空呢，其实就是他的左子树的的深度与右子树深度这两者中的最大值+1。这样一听似乎就豁然开朗了。

2.解题代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


int maxDepth(struct TreeNode* root){
    if(root==NULL)
    {
        return 0;
    }
    int left_maxDepth=maxDepth(root->left);
    int right_maxDepth=maxDepth(root->right);
    return left_maxDepth>right_maxDepth?left_maxDepth+1:right_maxDepth+1;
}

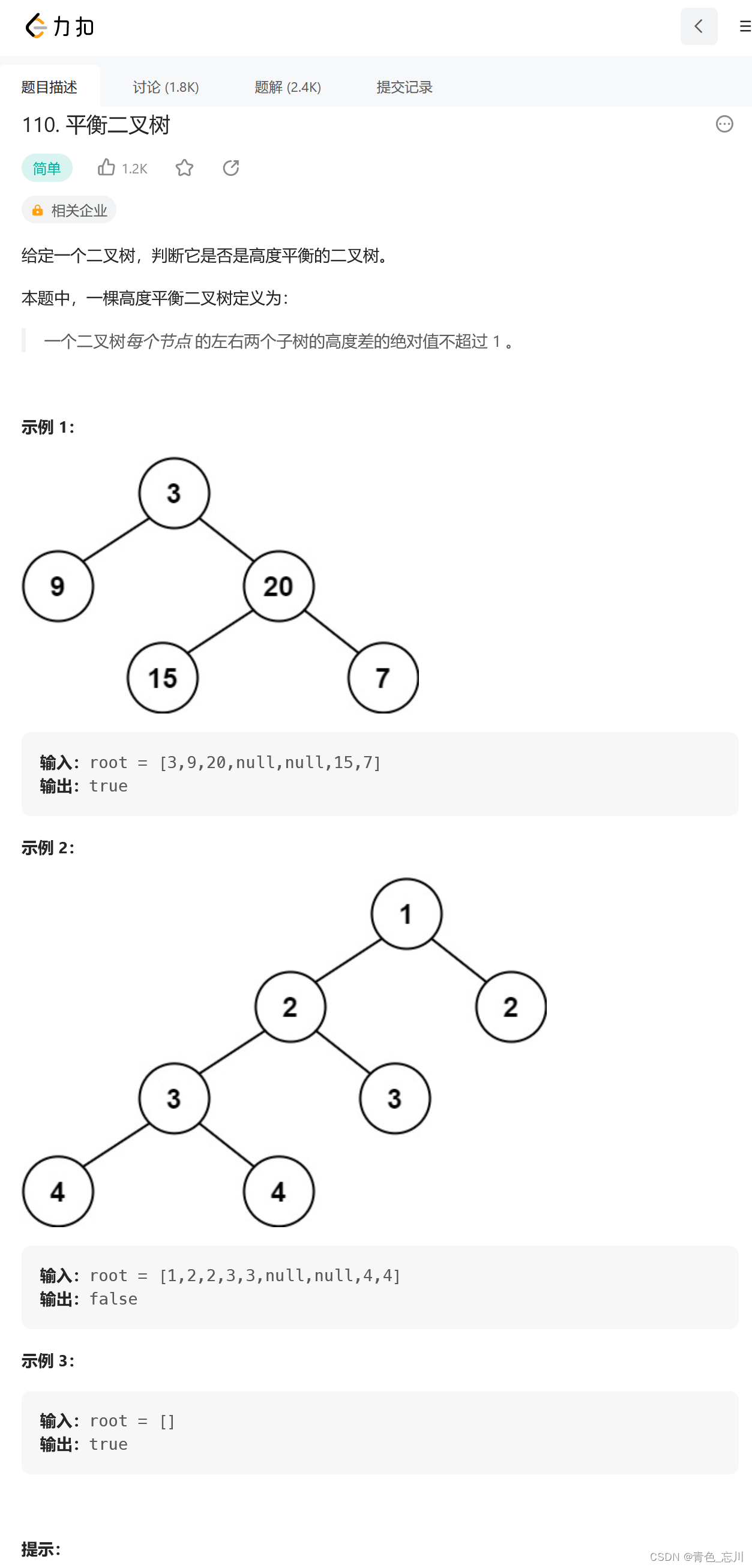
五、力扣第110题：平衡二叉树

题目链接：力扣

题目描述：

1.解题思路

对于这道题我们得先搞清楚平衡二叉树的定义，一棵树中的每一个结点他的左右子树高度差不超过1。我们在这里很容易想当然的就判断一下一棵树的左子树的深度，右子树的深度，然后做差求绝对值，其实这里就忽略了左右子树是否都满足平衡二叉树的定义。因为他是要求每一棵树都要满足定义的。在这里，我们就发现上一道题就有用起来了。我们直接使用上一道题的函数。然后再里面再套一层递归就可以解决问题了

2.解题代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
int maxDepth(struct TreeNode* root){
    if(root==NULL)
    {
        return 0;
    }
    int left_maxDepth=maxDepth(root->left);
    int right_maxDepth=maxDepth(root->right);
    return left_maxDepth>right_maxDepth?left_maxDepth+1:right_maxDepth+1;
}
bool isBalanced(struct TreeNode* root){
    if(root==NULL)
    {
        return true;
    }
    int leftDepth=maxDepth(root->left);
    int rightDepth=maxDepth(root->right);
    return abs(leftDepth-rightDepth)<2
        && isBalanced(root->left)
        && isBalanced(root->right);
}