1.概述

逻辑回归，是一种线性分类器。其本质是由线性回归变化而来的，一种广泛使用于分类问题中的广义回归算法。

最小二乘法就是用来求解线性回归中参数的数学方法。

2.sklearn中的逻辑回归

（1）逻辑回归分类器（又叫logit回归，最大熵分类器）
（2）带交叉验证的逻辑回归分类器
（3）利用梯度下降求解的线性分类器（SVM，逻辑回归等等）

3. linear_model.LogisticRegression

其中， 表示求解出来的一组参数，m是样本的个数， 是样本i上真实的标签， 是样本i上，基于参数 计算出来的逻辑回归返回值， 是样本i各个特征的取值。

这就是我们的交叉熵函数。我们希望将极大值问题转换为极小值问题，因此我们对logP取负，就得到了

3.重要参数

（1）penalty & C

正则化是用来防止模型过拟合的过程，常用的有L1正则化和L2正则化两种选项，分别通过在损失函数后加上参数向量的L1范式和L2范式的倍数来实现。

其中L1范式表现为参数向量中的每个参数的绝对值之和，L2范数表现为参数向量中的每个参数的平方和的开方值。
其中 是我们之前提过的损失函数，C是用来控制正则化程度的超参数，n是方程中特征的总数，也是方程中参数的总数，j代表每个参数。

L1正则化和L2正则化虽然都可以控制过拟合，但它们的效果并不相同。当正则化强度逐渐增大（即C逐渐变小），参数 的取值会逐渐变小，但L1正则化会将参数压缩为0，掌管了参数的“稀疏性”。，L2正则化只会让参数尽量小，不会取到0。

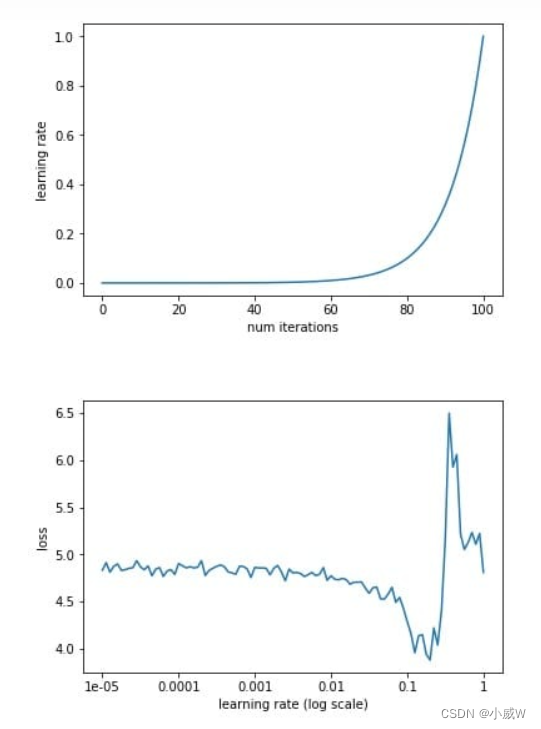
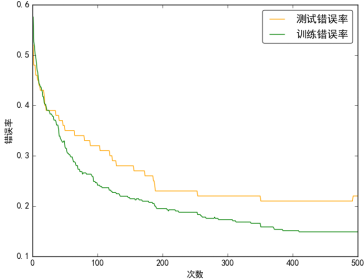
（2）max_iter

逻辑回归的数学目的是求解能够让模型最优化，拟合程度最好的参数 的值，即求解能够让损失函数 最小化的值。
梯度下降求解逻辑回归

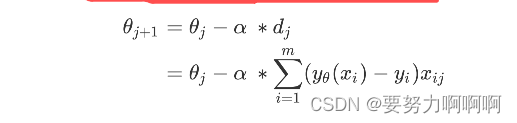
其中 是第j次迭代后的参数向量， 是第j次迭代是的参数向量， 被称为步长，控制着每走一步（每迭代一次）后 的变化，并以此来影响每次迭代后的梯度向量的大小和方向。

（2）class_weight

样本不平衡