顺序表中基本操作的具体思路与实现（C语言版）

news2024/9/21 6:59:31

顺序表中基本操作的具体思路与实现（C语言版）

      • 一、操作前的准备工作
        • （1）定义操作算法中用到的预定义常量和类型
        • （2）定义线性表中可能拥有的元素的最大个数
        • （3）定义顺序表类型
      • 二、具体操作的实现
        • （1）创建顺序表
        • （2）初始化顺序表
        • （3）销毁顺序表
        • （4）清除顺序表
        • （5）求顺序表的长度
        • （6）判断顺序表是否为空
        • （7）顺序表的按位置查找（根据位置position获取相应位置数据元素的值）
        • （8）顺序表的按值查找
            • 方法一：使用for循环
            • 方法二：使用while语句
        • （9）顺序表的插入操作
        • （10）顺序表的按位置删除操作
        • （11）顺序表的求前驱节点操作
        • （12）顺序表的求后继节点操作
        • （13）显示顺序表操作
      • 三、全部代码及其运行结果

一、操作前的准备工作

（1）定义操作算法中用到的预定义常量和类型

//函数结果状态代码：
#define TURE 1
#define FALSE 0
#define OK  1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2

//Status是函数的类型，其值是函数结果状态代码
typedef int Status;
typedef int Elemtype;

（2）定义线性表中可能拥有的元素的最大个数

#define MAXSIZE 5

（3）定义顺序表类型

typedef struct {
	Elemtype *elem;
	int length; //当前顺序表中实际拥有的元素个数，即当前顺序表的长度
}SqList;

二、具体操作的实现

（1）创建顺序表

//创建顺序表
Status List_Creat(SqList* L,int n)
{
    int i;
    if (n < 1 || n > MAXSIZE)
    {
        return ERROR;
    }
    L->elem = (Elemtype*)malloc(sizeof(Elemtype) * MAXSIZE);
    L->length = n;
    for (i = 0; i < L->length; i++)
    {
        int temp;
        int number = i + 1;
        printf("请输入顺序表中的第%d个元素个数：\n", number);
        scanf("%d", &temp);
        L->elem[i] = temp;
    }
    return OK;
}

（2）初始化顺序表

malloc(m)函数，开辟m字节长度的地址空间，并返回这段空间的首地址

sizeof(x)函数，计算变量x的长度

思路：
①为顺序表动态分配空间
②如果内存分配失败
③空表长度为0

Status InitList_Sq(SqList *L) {
	//malloc(m)函数，开辟m字节长度的地址空间，并返回这段空间的首地址
	//sizeof(x)函数，计算变量x的长度
    //①为顺序表动态分配空间
	L->elem = (Elemtype*)malloc(sizeof(Elemtype)*MAXSIZE);  
	//②如果内存分配失败
    if (!(L->elem)) {                                            
        //exit(0) 表示程序正常退出
        //exit⑴/exit(-1)表示程序异常退出
        //exit() 结束当前进程/当前程序
        //在整个程序中只要调用exit就结束
        return ERROR;
        exit(OVERFLOW);
    }
    //③空表长度为0
    L->length = 0;
    return OK;
}

（3）销毁顺序表

Status DestroyList(SqList *L){
    if (!L->elem) {
        return ERROR;
    }
    else
    {
        free(L->elem);
        return OK;
    }
}

（4）清除顺序表

Status ClearList(SqList *L) {
    if (!L->elem) {
        return ERROR;
    }
    else
    {
        L->length = 0;
        return OK;
    }
}

（5）求顺序表的长度

Status GetLength(SqList *L)
{
    return L->length;
}

（6）判断顺序表是否为空

Status IsEmpty(SqList *L) {
    if (L->length == 0) {
        return 1;
    }
    else {
        return 0;
    }
}

（7）顺序表的按位置查找（根据位置position获取相应位置数据元素的值）

注意：此处的position指的是逻辑位序，从1开始，而物理位序即下标从0开始

Status GetElme(SqList *L, int position, Elemtype *e) {
    //判断position的值是否合理，若不合理，返回error
    if (position < 1 || position > L->length) {
        return ERROR;
    }
    *e = L->elem[position - 1];//position - 1的单元存放着第position个数据
    return OK;
}

（8）顺序表的按值查找

在线性表L中查找与指定值e相同的数据元素的位置

从表的一端开始，逐个进行记录的关键字和给定值的比较。

找到返回该元素的位置序号，未找到，返回0。

方法一：使用for循环
Status LocateElme(SqList *L,Elemtype e){
    //法一：使用for循环
    //在线性表L中查找值为e的数据元素，返回其序号(是第几个元素)
    for (int i = 0; i < L->length; i++)
    {
        if (L->elem[i] == e) {
            return i + 1;//查找成功，返回序号
        }
    }
    return 0;//查找失败,返回0
}
方法二：使用while语句
Status LocateElme(SqList *L,Elemtype e){
    //法二：使用while语句
    //在线性表l中查找值为e的数据元素，返回其序号(是第几个元素)
    int i = 0;
    while (i < L->length && L->elem[i] != e)
    {
        i++;
    }
    if (i < L->length) {
        return i + 1;//查找成功，返回序号
    }
    return 0;//查找失败,返回0
}

（9）顺序表的插入操作

  • 顺序表的插入的含义：线性表的插入运算是指在表的第i (1 <= i <= n+1)个位置上，插入一个新结点e，使长度为n的线性表(a1,…,ai - 1, ai,…,an)变成长度为n+1的线性表(a1,…,ai-1,e,ai,…,an)
  • 算法思想:
    ①判断插入位置i是否合法。
    ②判断顺序表的存储空间是否已满，若已满返回ERROR。
    ③将第n至第i位的元素依次向后移动一个位置，空出第i个位置。
    ④将要插入的新元素e放入第i个位置。
    ⑤表长加1，插入成功返回OK。
Status ListInsert_Sq(SqList *L, int i, Elemtype e) {
    if (i < 1 || i > L->length + 1)
    {
        return ERROR; //i值不合法
    }
    if (L->length == MAXSIZE)
    {
        return ERROR; //当前存储空间已满
    }
    for (int j = L->length - 1; j >= i - 1; j--)
    {
        L->elem[j + 1] = L->elem[j]; //插入位置及之后的元素后移
    }
    L->elem[i - 1] = e;
    L->length++;
    return OK;
}

（10）顺序表的按位置删除操作

  • 顺序表的删除运算的含义：顺序表的删除运算是指将表的第i(1 <= i <= n+1)个结点删除，使长度为n的线性表(a1,…,ai-1,ai,ai+1,…,an)变成长度为n-1的线性表(a1,…,ai-1,ai+1,…,an)。
  • 算法思想:
    ①判断删除位置i是否合法(合法值为1<=i<=n+1)。
    ②将第i+1至第n位的元素依次向前移动一个位置。
    ③表长减1, 删除成功返回OK。
Status ListDelete_Sq(SqList *L, int i) {
    if (i < 1 || i > L->length)
    {
        return ERROR; //i值不合法
    }
    int j;
    for (j = i; j < L->length; j++)
    {
        L->elem[j - 1] = L->elem[j]; //插入位置及之后的元素后移
    }
    L->length--;
    return OK;
}

（11）顺序表的求前驱节点操作

Status List_Prior(SqList* L, int i) {
    if (i < 2 || i > L->length)
    {
        return ERROR;
    }
    return L->elem[i - 2];
}

（12）顺序表的求后继节点操作

Status List_Next(SqList* L, int i) {
    if (i < 1 || i > L->length - 1)
    {
        return ERROR;
    }
    return L->elem[i];
}

（13）显示顺序表操作

void Show_Sq(SqList* L) {
    for (int i = 0; i < L->length; i++)
    {
        printf("%d\t", L->elem[i]);
    }
}

三、全部代码及其运行结果

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>     
//操作算法中用到的预定义常量和类型
//函数结果状态代码：
#define TURE 1
#define FALSE 0
#define OK  1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2

//Status是函数的类型，其值是函数结果状态代码
typedef int Status;
typedef int Elemtype;

//定义线性表中可能拥有的元素的最大个数
#define MAXSIZE 5

//定义顺序表类型
typedef struct {
	Elemtype *elem;
	int length; //当前顺序表中实际拥有的元素个数，即当前顺序表的长度
}SqList;

//创建顺序表
Status List_Creat(SqList* L,int n)
{
    int i;
    if (n < 1 || n > MAXSIZE)
    {
        return ERROR;
    }
    L->elem = (Elemtype*)malloc(sizeof(Elemtype) * MAXSIZE);
    L->length = n;
    for (i = 0; i < L->length; i++)
    {
        int temp;
        int number = i + 1;
        printf("请输入顺序表中的第%d个元素个数：\n", number);
        scanf("%d", &temp);
        L->elem[i] = temp;
    }
    return OK;
}

//初始化顺序表
Status InitList_Sq(SqList *L) {
	//malloc(m)函数，开辟m字节长度的地址空间，并返回这段空间的首地址
	//sizeof(x)函数，计算变量x的长度
    //①为顺序表动态分配空间
	L->elem = (Elemtype*)malloc(sizeof(Elemtype)*MAXSIZE);  
	//②如果内存分配失败
    if (!(L->elem)) {                                            
        //exit(0) 表示程序正常退出
        //exit⑴/exit(-1)表示程序异常退出
        //exit() 结束当前进程/当前程序
        //在整个程序中只要调用exit就结束
        return ERROR;
        exit(OVERFLOW);
    }
    //③空表长度为0
    L->length = 0;
    return OK;
}

//销毁顺序表
Status DestroyList(SqList *L){
    if (!L->elem) {
        return ERROR;
    }
    else
    {
        free(L->elem);
        return OK;
    }
}

//清除顺序表
Status ClearList(SqList *L) {
    if (!L->elem) {
        return ERROR;
    }
    else
    {
        L->length = 0;
        return OK;
    }
}

//求顺序表的长度
Status GetLength(SqList *L)
{
    return L->length;
}

//判断顺序表是否为空
Status IsEmpty(SqList *L) {
    if (L->length == 0) {
        return 1;
    }
    else {
        return 0;
    }
}

//顺序表的取值（根据位置position获取相应位置数据元素的值）
//注意：此处的position指的是逻辑位序，从1开始，而物理位序即下标从0开始
Status GetElme(SqList *L, int position, Elemtype *e) {
    //判断position的值是否合理，若不合理，返回error
    if (position < 1 || position > L->length) {
        return ERROR;
    }
    *e = L->elem[position - 1];//position - 1的单元存放着第position个数据
    return OK;
}

//顺序表的按值查找
//在线性表L中查找与指定值e相同的数据元素的位置
//从表的一端开始，逐个进行记录的关键字和给定值的比较。找到返回该元素的位置序号，未找到，返回0。
Status LocateElme(SqList *L,Elemtype e){
    //法一：使用for循环
    //在线性表L中查找值为e的数据元素，返回其序号(是第几个元素)
    //for (int i = 0; i < L->length; i++)
    //{
    //    if (L->elem[i] == e) {
    //        return i + 1;//查找成功，返回序号
    //    }
    //}
    //return 0;//查找失败,返回0

    //法二：使用while语句
    //在线性表l中查找值为e的数据元素，返回其序号(是第几个元素)
    int i = 0;
    while (i < L->length && L->elem[i] != e)
    {
        i++;
    }
    if (i < L->length) {
        return i + 1;//查找成功，返回序号
    }
    return 0;//查找失败,返回0
}

//顺序表的插入
//插入位置在最后
//插入位置在中间
//插入位置在最前面
//顺序表的插入的含义：线性表的插入运算是指在表的第i(1<=i<=n+1)个位置上，插入-个新结点e, 
//使长度为n的线性表(a1,...,ai - 1, ai,...,an)变成长度为n+1的线性表(a1,...,ai-1,e,ai,...,an)
//算法思想:
//①判断插入位置i是否合法。
//②判断顺序表的存储空间是否已满，若已满返回ERROR。
//③将第n至第i位的元素依次向后移动一个位置，空出第i个位置。
//④将要插入的新元素e放入第i个位置。
//⑤表长加1，插入成功返回OK。
Status ListInsert_Sq(SqList *L, int i, Elemtype e) {
    if (i < 1 || i > L->length + 1)
    {
        return ERROR; //i值不合法
    }
    if (L->length == MAXSIZE)
    {
        return ERROR; //当前存储空间已满
    }
    for (int j = L->length - 1; j >= i - 1; j--)
    {
        L->elem[j + 1] = L->elem[j]; //插入位置及之后的元素后移
    }
    L->elem[i - 1] = e;
    L->length++;
    return OK;
}

//顺序表的按位置删除
//线性表的删除运算是指将表的第i(1<=i<=n+1)个结点删除
//使长度为n的线性表(a1,...,ai-1,ai,ai+1,...,an)
//变成长度为n-1的线性表(a1,...,ai-1,ai+1,...,an)
//算法思想:
//①判断删除位置i是否合法(合法值为1<=i<=n+1)。
//②将第i+1至第n位的元素依次向前移动一个位置。
//③表长减1, 删除成功返回OK。
Status ListDelete_Sq(SqList *L, int i) {
    if (i < 1 || i > L->length)
    {
        return ERROR; //i值不合法
    }
    int j;
    for (j = i; j < L->length; j++)
    {
        L->elem[j - 1] = L->elem[j]; //插入位置及之后的元素后移
    }
    L->length--;
    return OK;
}

//求前驱
Status List_Prior(SqList* L, int i) {
    if (i < 2 || i > L->length)
    {
        return ERROR;
    }
    return L->elem[i - 2];
}

//求后继
Status List_Next(SqList* L, int i) {
    if (i < 1 || i > L->length - 1)
    {
        return ERROR;
    }
    return L->elem[i];
}

//显示顺序表
void Show_Sq(SqList* L) {
    for (int i = 0; i < L->length; i++)
    {
        printf("%d\t", L->elem[i]);
    }
}

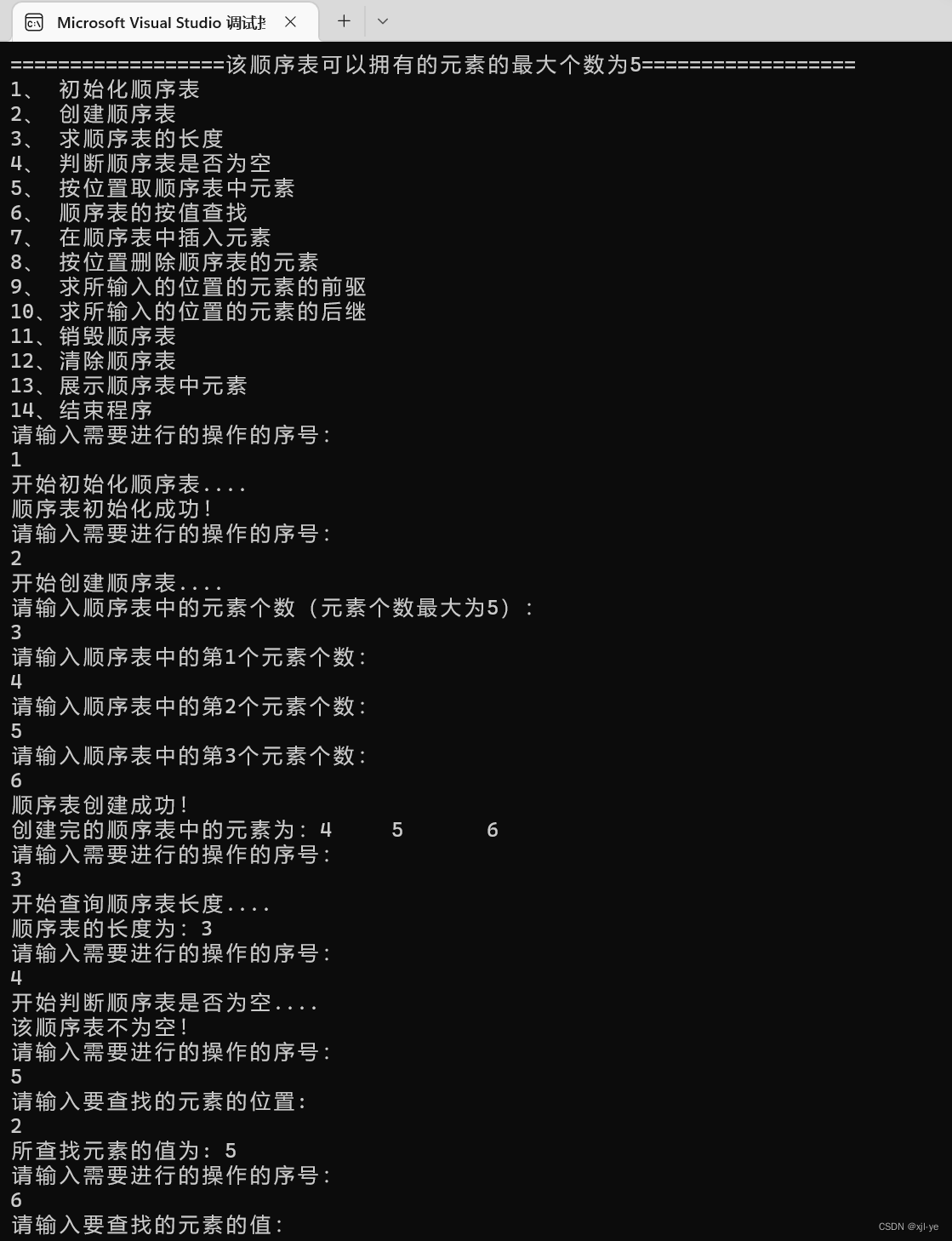
int main() {
    printf("==================该顺序表可以拥有的元素的最大个数为5==================\n");
    SqList L;
    L.length = 0;
    int select,status;
    printf("1、 初始化顺序表\n");
    printf("2、 创建顺序表\n");
    printf("3、 求顺序表的长度\n");
    printf("4、 判断顺序表是否为空\n");
    printf("5、 按位置取顺序表中元素\n");
    printf("6、 顺序表的按值查找\n");
    printf("7、 在顺序表中插入元素\n");
    printf("8、 按位置删除顺序表的元素\n");
    printf("9、 求所输入的位置的元素的前驱\n");
    printf("10、求所输入的位置的元素的后继\n");
    printf("11、销毁顺序表\n");
    printf("12、清除顺序表\n");
    printf("13、展示顺序表中元素\n");
    printf("14、结束程序\n");
    while (1)
    {
        printf("请输入需要进行的操作的序号：\n");
        scanf("%d", &select);
        switch (select)
        {
            case 1: {
                        printf("开始初始化顺序表....\n");
                        status = InitList_Sq(&L);
                        if (status == OK)
                        {
                            printf("顺序表初始化成功！\n");
                        }
                        if (status == ERROR)
                        {
                            printf("顺序表内存分配失败！顺序表初始化失败！\n");
                        }
                        break;
                    }

            case 2: {
                        int n;
                        printf("开始创建顺序表....\n");
                        printf("请输入顺序表中的元素个数（元素个数最大为5）：\n");
                        scanf("%d", &n);
                        status = List_Creat(&L,n);
                        if (status == OK)
                        {
                            printf("顺序表创建成功！\n");
                            printf("创建完的顺序表中的元素为：");
                            Show_Sq(&L);
                            printf("\n");
                        }
                        if (status == ERROR)
                        {
                            printf("元素个数不符合要求！\n");
                        }
                        break;
                    }

            case 3: {
                        int now = IsEmpty(&L);
                        if (now == 1)
                        {
                            printf("请先创建一个顺序表！");
                            break;
                        }
                        printf("开始查询顺序表长度....\n");
                        int result = GetLength(&L);
                        printf("顺序表的长度为：%d\n", result);
                        break;
                    }

            case 4: {
                        printf("开始判断顺序表是否为空....\n");
                        int result = IsEmpty(&L);
                        if (result == 1) 
                        {
                            printf("该顺序表为空！\n");
                        }
                        if (result == 0)
                        {
                            printf("该顺序表不为空！\n");
                        }
                        break;
                    }

            case 5: {
                        int now = IsEmpty(&L);
                        if (now == 1)
                        {
                            printf("请先创建一个顺序表！");
                            break;
                        }
                        int position;
                        Elemtype e = 0;
                        printf("请输入要查找的元素的位置:\n");
                        scanf("%d",&position);
                        int result = GetElme(&L, position, &e);
                        if (result == ERROR)
                        {
                            printf("输入的位置的值不合理！\n");
                        }
                        if (result == OK)
                        {
                            printf("所查找元素的值为: %d\n",e);
                        }
                        break;
                    }

            case 6: {
                        int now = IsEmpty(&L);
                        if (now == 1)
                        {
                            printf("请先创建一个顺序表！");
                            break;
                        }
                        Elemtype e;
                        printf("请输入要查找的元素的值：\n");
                        scanf("%d", &e);
                        int result = LocateElme(&L, e);
                        if (result == 0)
                        {
                            printf("查找失败！\n");
                        }
                        if (result != 0)
                        {
                            printf("要查找的元素的位置为: %d\n", result);
                        }
                        break;
                    }

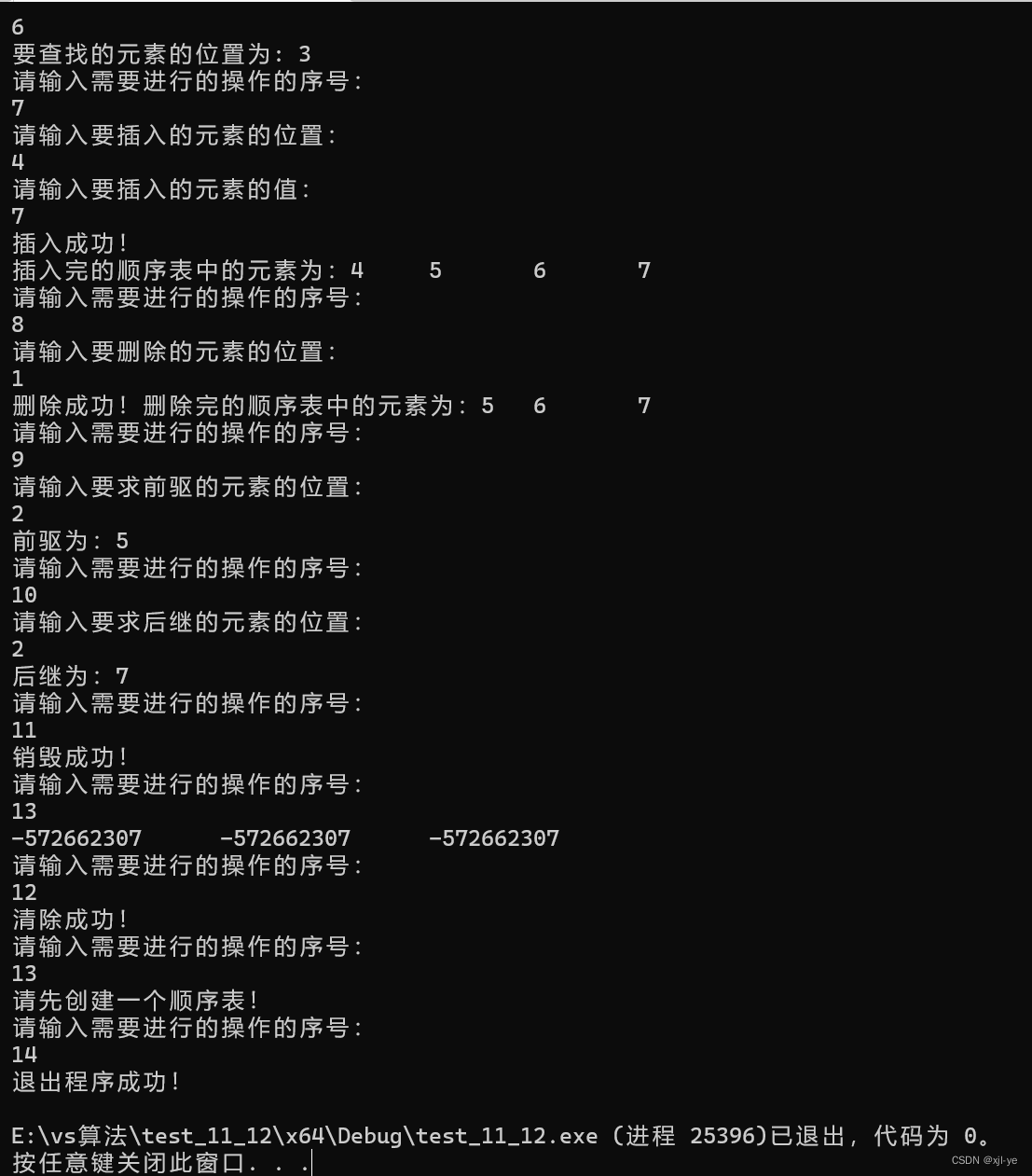
            case 7: {
                        int now = IsEmpty(&L);
                        if (now == 1)
                        {
                            printf("请先创建一个顺序表！");
                            break;
                        }
                        Elemtype e;
                        int position;
                        printf("请输入要插入的元素的位置：\n");
                        scanf("%d", &position);
                        printf("请输入要插入的元素的值：\n");
                        scanf("%d", &e);
                        int result = ListInsert_Sq(&L,position,e);
                        if (result == ERROR)
                        {
                            printf("插入失败！\n");
                        }
                        if (result == OK)
                        {
                            printf("插入成功！\n");
                            printf("插入完的顺序表中的元素为：");
                            Show_Sq(&L);
                            printf("\n");
                        }
                        break;
                    }
            case 8: {
                        int now = IsEmpty(&L);
                        if (now == 1)
                        {
                            printf("请先创建一个顺序表！");
                            break;
                        }
                        int position;
                        printf("请输入要删除的元素的位置：\n");
                        scanf("%d", &position);
                        int result = ListDelete_Sq(&L, position);
                        if (result == ERROR)
                        {
                            printf("删除失败！\n");
                        }
                        if (result == OK)
                        {
                            printf("删除成功！");
                            printf("删除完的顺序表中的元素为：");
                            Show_Sq(&L);
                            printf("\n");
                        }
                        break;
                    }
            case 9: { 
                        int now = IsEmpty(&L);
                        if (now == 1)
                        {
                            printf("请先创建一个顺序表！");
                            break;
                        }
                        int position;
                        printf("请输入要求前驱的元素的位置：\n");
                        scanf("%d", &position);
                        int result = List_Prior(&L, position);
                        if (result == ERROR)
                        {
                            printf("输入的位置错误！\n");
                        }
                        if (result != ERROR)
                        {
                            printf("前驱为：%d\n",result);
                        }
                        break;
                    }

            case 10: {
                        int now = IsEmpty(&L);
                        if (now == 1)
                        {
                            printf("请先创建一个顺序表！");
                            break;
                        }
                        int position;
                        printf("请输入要求后继的元素的位置：\n");
                        scanf("%d", &position);
                        int result = List_Next(&L, position);
                        if (result == ERROR)
                        {
                            printf("输入的位置错误！\n");
                        }
                        if (result != ERROR)
                        {
                            printf("后继为：%d\n", result);
                        }
                        break;
                    }
            case 11: {
                        int result = DestroyList(&L);
                        if (result == ERROR)
                        {
                            printf("销毁失败！顺序表还未创建！\n");
                        }
                        if (result == OK)
                        {
                            printf("销毁成功！\n");
                        }
                        break;
                    }

            case 12: {
                        int result = ClearList(&L);
                        if (result == ERROR)
                        {
                            printf("清除失败！顺序表还未创建！\n");
                        }
                        if (result == OK)
                        {
                            printf("清除成功！\n");
                        }
                        break;
                    }

            case 13: { 
                        int now = IsEmpty(&L);
                        if (now == 1)
                        {
                            printf("请先创建一个顺序表！");
                            break;
                        }
                        Show_Sq(&L);
                        printf("\n");
                        break;
                    }

            case 14: {
                        printf("退出程序成功！\n");
                        return 0;
                    }

            default: {
                        printf("请输入1~14内的整数！\n");
                        break;
                    }
        }

    }

}

在这里插入图片描述
在这里插入图片描述
嘿嘿，看到这里就说明你全部都看完啦！超详细的顺序表操作你学废了吗~请添加图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/132999.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

ZC706P+ADRV9009连接RADIOVERSE详解之一

ZC706P+ADRV9009连接RADIOVERSE详解之一

第一步是&#xff1a;安装WINDOWS软件。 从下面网页里面下载所需要的软件和文件&#xff1a; https://www.analog.com/en/design-center/landing-pages/001/transceiver-evaluation-software.html 下载下图中的软件&#xff0c;这是运行在WINDOWS系统上的&#xff0c;通过网…
阅读更多...
寒假本科创新学习——机器学习（一）

寒假本科创新学习——机器学习（一）

绪论1.1什么是机器学习1.1.1 Arthur Samuel给出的定义1.1.2 显著式编程和非显著式编程1.1.3 Tom Mitshell给出的定义1.2基本术语1.1什么是机器学习 1.1.1 Arthur Samuel给出的定义 Arthur Samuel是机器学习领域的先驱之一&#xff0c; 他编写了世界上第一个棋类游戏的人工智能…
阅读更多...
LaTeX公式与MathType公式如何快速转换

LaTeX公式与MathType公式如何快速转换

目录 一、官网下载链接 二、将MathType公式转换为LaTex公式&#xff1a; 三、将LaTex公式转换为MathType公式&#xff1a; 现在越来越多的人选择使用MathType来编辑公式&#xff0c;有时在MathType公式之间要与LaTex公式之间相互转换。如果公式比较少时&#xff0c;可以直接…
阅读更多...
ORB-SLAM2 --- MapPoint::ComputeDistinctiveDescriptors 函数

ORB-SLAM2 --- MapPoint::ComputeDistinctiveDescriptors 函数

目录 一、函数作用 二、函数步骤 三、code 四、函数解析 一、函数作用 计算地图点最具代表性的描述子。 由于一个地图点会被许多相机观测到&#xff0c;因此在插入关键帧后&#xff0c;需要判断是否更新代表当前点的描述子&#xff0c;先获得当前点的所有描述子&#xff…
阅读更多...
毕业设计-微博评论文本情感分析，SVM+朴素贝叶斯+AdaBoost，含完整项目文档

毕业设计-微博评论文本情感分析，SVM+朴素贝叶斯+AdaBoost，含完整项目文档

基于AdaBoost算法的情感分析研究 完整代码及文档下载地址&#xff1a;毕业设计-微博评论文本情感分析 此项目为本科毕业设计项目&#xff0c;大家借鉴一下思路就好 大学时没有好好学算法&#xff0c;毕竟那些树、图实在提不起兴趣&#xff0c;好在毕业设计选择了个机器学习算…
阅读更多...
rabbitmq基础9——流控、镜像队列

rabbitmq基础9——流控、镜像队列

文章目录一、流控1.1 流控机制1.2 流控原理1.3 流控状态显示1.4 流控对象1.5 性能提升二、镜像队列2.1 机制原理2.1.1 集群结构2.2 镜像结构2.2.1 组播GM2.2.1.1 实现原理2.2.1.2 加入新节点2.2.1.3 节点宕机的影响2.3 配置镜像队列2.3.1 定义参数2.3.2 命令配置2.3.4 相关命令…
阅读更多...
数字验证学习笔记——SystemVerilog芯片验证20 ——线程间的通信

数字验证学习笔记——SystemVerilog芯片验证20 ——线程间的通信

一、线程间的通信 测试平台中的所有线程都需要同步并交换数据。一个线程需要等待另一个。多个线程可能同时访问同一个资源。线程之间可能需要交换数据。所有这些数据交换和同步称之为线程间的通信&#xff08;IPC&#xff09;。 1.1 event 事件 Verilog 中&#xff0c;一个线…
阅读更多...
【好书推荐】车载以太网权威指南

【好书推荐】车载以太网权威指南

20年后&#xff0c;会令你失望的不是做过的事&#xff0c;而是你没做过的&#xff0c;所以解开帆索&#xff0c;从安全的港湾出发&#xff0c;乘风而行&#xff0c;去探索、去梦想、去发现&#xff01; Twenty years from now you will be more disappointed by the things tha…
阅读更多...
Linux系统 Ubuntu18.04安装的详细教程（提供18.04ubuntu镜像）

Linux系统 Ubuntu18.04安装的详细教程（提供18.04ubuntu镜像）

文章目录一、镜像安装二、vim更新 gcc ifconfig下载三、共享文件夹设置设置使用&#xff08;测试共享文件夹是否能使用&#xff0c;这步可以省略&#xff09;四、另外虚拟机名称全名、用户名镜像文件下载&#xff1a;链接&#xff1a;https://pan.baidu.com/s/12bEdRBwO1YbLt23…
阅读更多...
数学杂谈：圆上随机落点问题（一）

数学杂谈：圆上随机落点问题（一）

数学杂谈&#xff1a;圆上随机落点问题&#xff08;一&#xff09; 1. 问题描述2. 问题解答 1. 解法一&#xff1a;递推2. 解法二&#xff1a;受限制的均匀分布3. 数值模拟验证 3. 讨论 & 扩展 1. 问题描述 这道题其实很早之前自己做过一遍&#xff0c;然后前阵子发现苏神…
阅读更多...
【寒假每日一题】洛谷 P1079 [NOIP2012 提高组] Vigenère 密码

【寒假每日一题】洛谷 P1079 [NOIP2012 提高组] Vigenère 密码

题目链接&#xff1a;P1079 [NOIP2012 提高组] Vigenre 密码 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 题目描述 16 世纪法国外交家 Blaise de Vigenre 设计了一种多表密码加密算法 Vigenre 密码。Vigenre 密码的加密解密算法简单易用&#xff0c;且破译难度比较高&…
阅读更多...
类、对象与接口

类、对象与接口

前言 类、对象与接口 文章目录前言一、类与对象二、源文件声明的规则三、修饰符四、继承五、多态六、接口1、定义2、接口3、实现4、接口一、类与对象 类&#xff1a;定义一种全新的数据类型&#xff0c;包含一组变量&#xff08;数据&#xff09;和函数&#xff08;逻辑&#…
阅读更多...
【django】各种关联关系的模型类设计

【django】各种关联关系的模型类设计

文章目录前言一、级联操作二、一对多&#xff08;多对一&#xff09;的关联模型类设计1、学生表模型类设计2、渠道表模型类设计三、多对多的关联模型类设计1、课程表模型类设计四、多对多的关联模型类设计&#xff08;自定义中间表&#xff09;1、模型类设计课程表模型类设计报…
阅读更多...
神经网络的学习率如何选择？

神经网络的学习率如何选择？

文章目录学习率的概念学习率的选择方法参考资料学习率的概念 这里的学习率指的是深度学习神经网络训练过程中选取的一个超参数。 学习率作为参数更新时的一个乘数项&#xff0c;可以影响网络训练的速度&#xff0c;或者说是每次迈步的大小。 可以这样理解&#xff0c;如果学…
阅读更多...
ZC706P+ADRV9009连接RADIOVERSE详解之二

ZC706P+ADRV9009连接RADIOVERSE详解之二

上一个BLOG我们在WIN上安装了RADIOVERSE软件以及做好了SD卡映像。这篇文字我们记录ZC706ADRV9009硬件链接情况&#xff1a; 这里看到USB UART串口是可选的&#xff0c;主要是用来查看启动的系统log。 实际连接如下&#xff1a; 图中&#xff1a; 1&#xff0c;外接12V电源 2…
阅读更多...
Python数据结构与算法篇（三）-- 队列的实现和应用

Python数据结构与算法篇（三）-- 队列的实现和应用

1 队列 1.1 简单队列 队列是一种有次序的数据集合&#xff0c;其特征是新数据项的添加总发生在一端&#xff08;通常称为“尾rear”端&#xff09;&#xff1b;而现存数据项的移除总发生在另一端&#xff08;通常称为“首front”端&#xff09;。当一个元素被加入到队列之后&a…
阅读更多...
头歌作业之排序1、2、3、4

头歌作业之排序1、2、3、4

&#xff08;PS&#xff1a;直接拿的友友zy的&#xff09; 一个不知名大学生&#xff0c;江湖人称菜狗 original author: jacky Li Email : 3435673055qq.com Time of completion&#xff1a;2023.1.1 Last edited: 2023.1.1 目录 &#xff08;PS&#xff1a;直接拿的友友的&a…
阅读更多...
SCI论文解读复现【NO.2】基于注意机制的YOLOv5改进算法在行星图像中的应用(代码已复现)

SCI论文解读复现【NO.2】基于注意机制的YOLOv5改进算法在行星图像中的应用(代码已复现)

此前出了目标检测算法改进专栏&#xff0c;但是对于应用于什么场景&#xff0c;需要什么改进方法对应与自己的应用场景有效果&#xff0c;并且多少改进点能发什么水平的文章&#xff0c;为解决大家的困惑&#xff0c;此系列文章旨在给大家解读发表高水平学术期刊中的SCI论文&am…
阅读更多...
EMNLP22提示模板生成：GPS: Genetic Prompt Search for Efficient Few-shot Learning

EMNLP22提示模板生成：GPS: Genetic Prompt Search for Efficient Few-shot Learning

GPS: Genetic Prompt Search for Efficient Few-shot Learning 1 简介 Genetic Prompt Search (GPS) 通过提示改进少样本学习&#xff0c;它利用遗传算法自动搜索高性能提示 遗传提示搜索 (GPS) 算法&#xff0c;该算法使用生成模型逐渐改变提示&#xff0c;并根据它们在小型…
阅读更多...
C语言网刷题记录

C语言网刷题记录

作者&#xff1a;会敲代码的Steve 座右铭&#xff1a;博学笃志&#xff0c;切问静思。 大家好久不见啊&#xff0c;一看时间我已经好久没发文章了&#xff0c;最近在刷OJ题和学习&#xff1b;就没那么多心思把时间花在写文章上了&#xff0c;我对此感到很抱歉&#xff0c;本文呢…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023