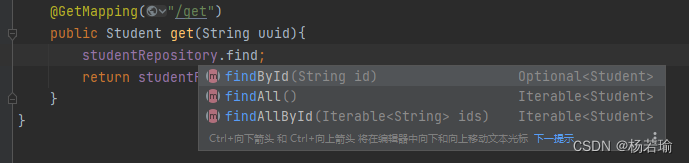
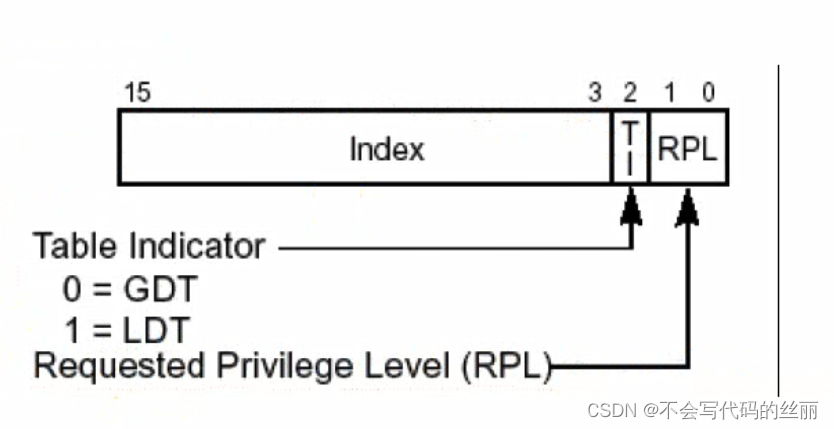
题目描述

有 N 堆石子，每堆的石子数量分别为 a1,a2,…,aN。

你可以对石子堆进行合并操作，将两个相邻的石子堆合并为一个石子堆，例如，如果 a=[1,2,3,4,5]，合并第 2,3 堆石子，则石子堆集合变为 a=[1,5,4,5]。

我们希望通过尽可能少的操作，使得石子堆集合中的每堆石子的数量都相同。

请你输出所需的最少操作次数。

本题一定有解，因为可以将所有石子堆合并为一堆。

输入格式

第一行包含整数 T，表示共有 T 组测试数据。

每组数据第一行包含整数 N。

第二行包含 N 个整数 a1,a2,…,aN。

输出格式

每组数据输出一行结果。

数据范围

输入输出样例及解释

思路

①对于每组数据，我们先统计这组数据中石子的总和，记为sum；

②显然，最终的组数一定是sum的约数，可以整除sum，因此我们从n开始枚举这个数（因为最多有n组，最简单的情况是，什么也不用做，但是此时也需要保证n是sum的约数）；

③之后，判断枚举的组数cnt是否满足题意，即，从头开始合并石子，如果能合并成第i堆且第i堆的石子数量小于等于sum/cnt，则说明可以合并当前堆，如果超过sum/cnt，说明不合题意，继续枚举。

代码

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn = 1e6 + 5;
int n, t, a[maxn] = {0};
bool check(int x){
	for(int i=1, s=0;i<=n;i++){
		s += a[i];
		if(s > x)	return false;
		else if(s == x){
			s = 0;
		}
	}
	return true;
}
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	cin>>t;
	while(t--){
		cin>>n;
		int sum = 0;
		for(int i=1;i<=n;i++){
			cin>>a[i];
			sum += a[i];
		}
		for(int i=n;i>=0;i--){
			if(sum % i == 0 && check(sum/i)){
				cout<<n-i<<endl;
			}
		}
	}
	return 0;
}