---

❤️前言

本文介绍两种基于分治思想的经典排序算法： 归并排序与快速排序

---

💘一、分治思想

分治思想，就是将原问题分解为几个规模较小但类似于原问题的子问题，递归地求解这些子问题，然后在合并这些子问题的解来建立原问题的解。

从上面的解释中我们可以看出，分而治之的思维是靠递归来实现的，所以说，分而治之是一种思维，而递归就是具体的实现。

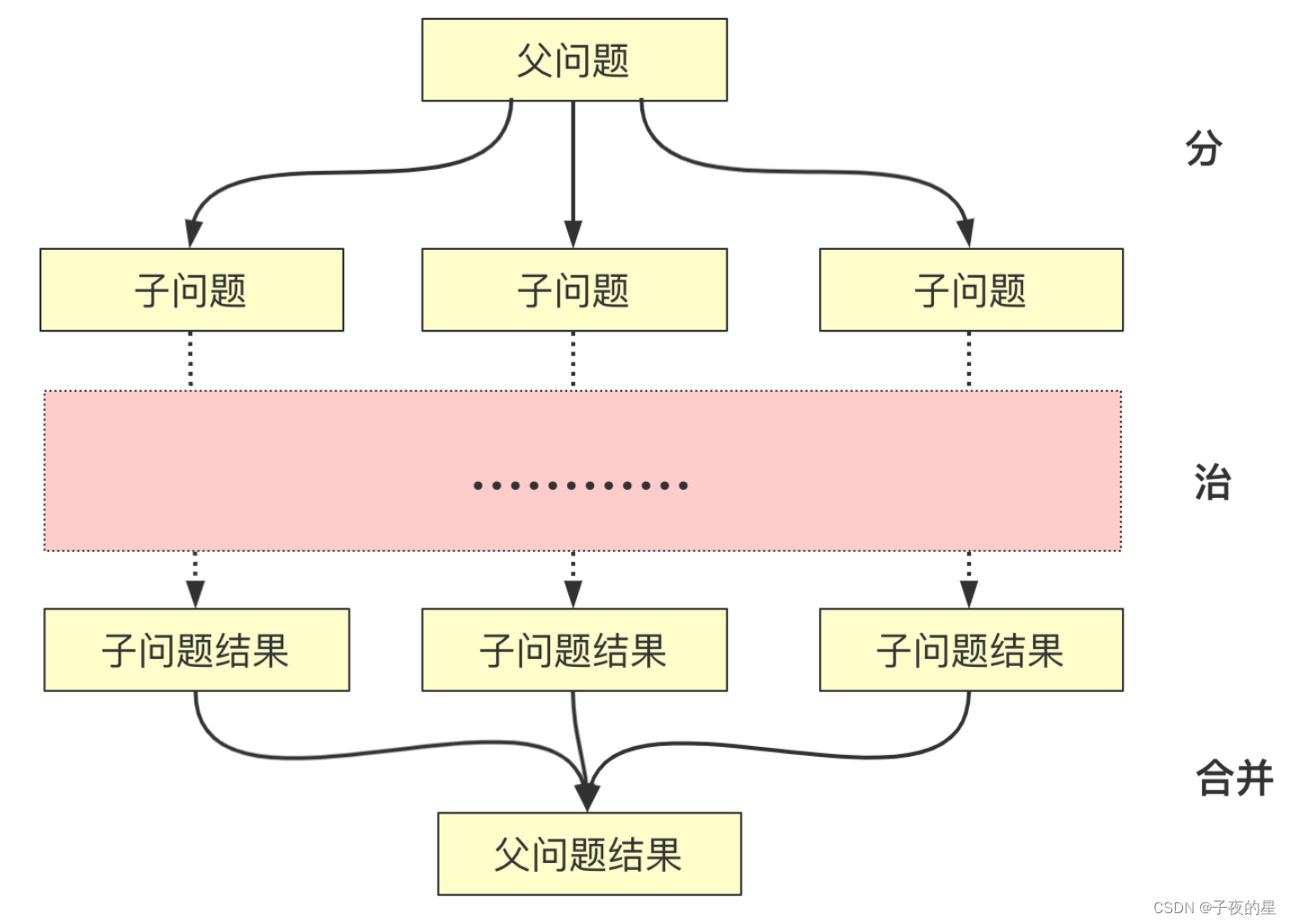
分而治之的实现具体有2个步骤：
1.找出基线条件，这种条件必须尽可能简单。
2. 不断将问题分解（或者说缩小规模），直到符合基线条件。

---

💞二、归并排序

1.实现方法

归并排序的核心思想是分治思想
分：将未排序的数组从中间分割成2部分，依次类推直至无法分割。
治：当无法再分割时，便可以对分区的元素进行两两合并
简而言之，就是左边排好序+右边排好序+归（合）并让整体有序
值得注意的是在对分区进行合并时，需要一个额外的辅助数组来暂存合并的结果，最后再复制到原数组中。

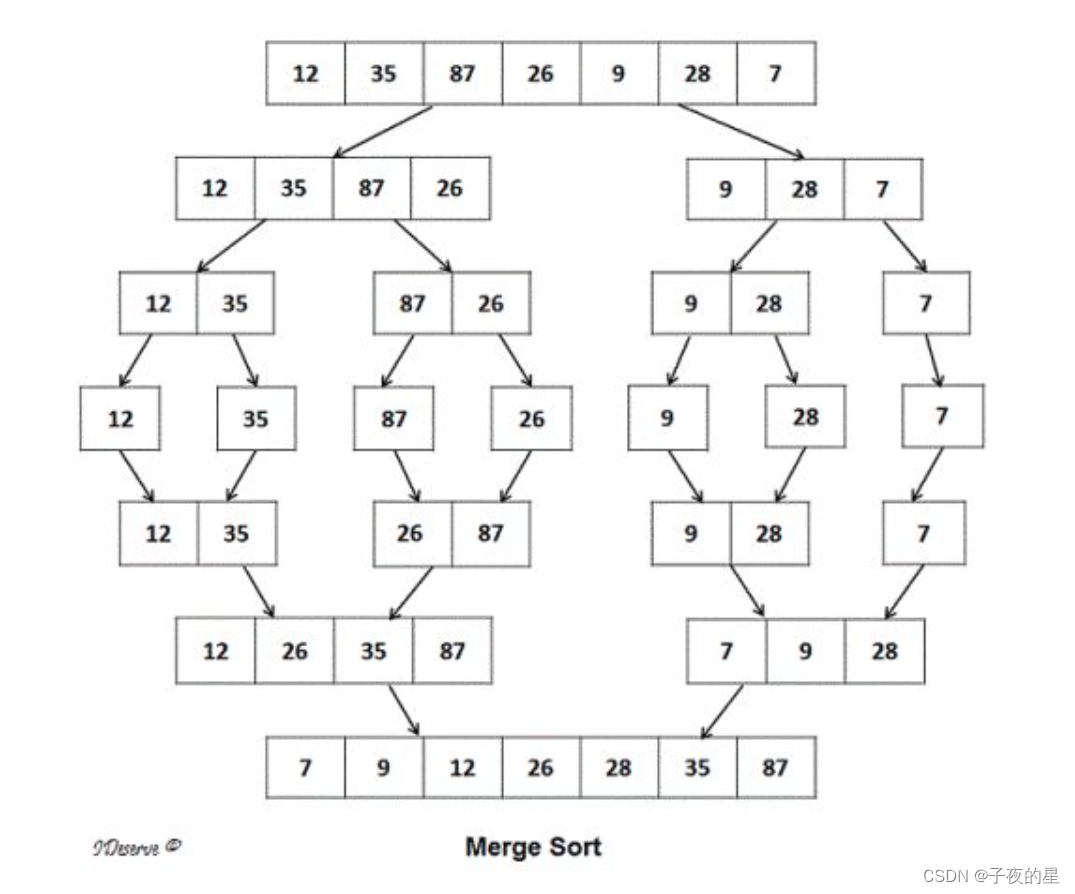
2.动图分析

3.代码模板

//合并函数
void merge(int arr[], int l, int mid, int r)
{
	int n = r - l + 1;
	//辅助数组
	int* help = (int*)malloc(n * sizeof(int));
	int index = 0;
	int p1 = l, p2 = mid + 1;
	while (p1 <= mid && p2 <= r) {
		if (arr[p1] <= arr[p2])
			help[index++] = arr[p1++];
		else
			help[index++] = arr[p2++];
	}
    while (p1 <= mid) {
        help[index++] = arr[p1++];
    }
    while (p2 <= r) {
        help[index++] = arr[p2++];
    }
    //复制到原数组
    for (int i = 0; i < n; i++) {
        arr[l + i] = help[i];
    }
}
//递归实现归并排序
void merge_sort(int arr[], int l, int r)
{
	if (l >= r)
		return;
	int mid = ( l + r  ) / 2;
	//排序左边
	merge_sort(arr, l, mid);
	//排序右边
	merge_sort(arr, mid + 1, r);
	//合并
	merge(arr, l, mid, r);
}

---

💖三、快速排序

1.实现方法

快速排序的核心思想同样也是分治思想
但是快速排序在分组的时候已经根据元素的大小来分组了，因此，合并时快速排序只需要把两个分组合并起来就可以了。而归并排序则需要对两个有序的数组根据大小进行合并。

快速排序的实现：
1、先调整区间，使小于等于基数x的在左边 ，大于等于基数x 的在右边。
2、递归处理基数x的左右段。

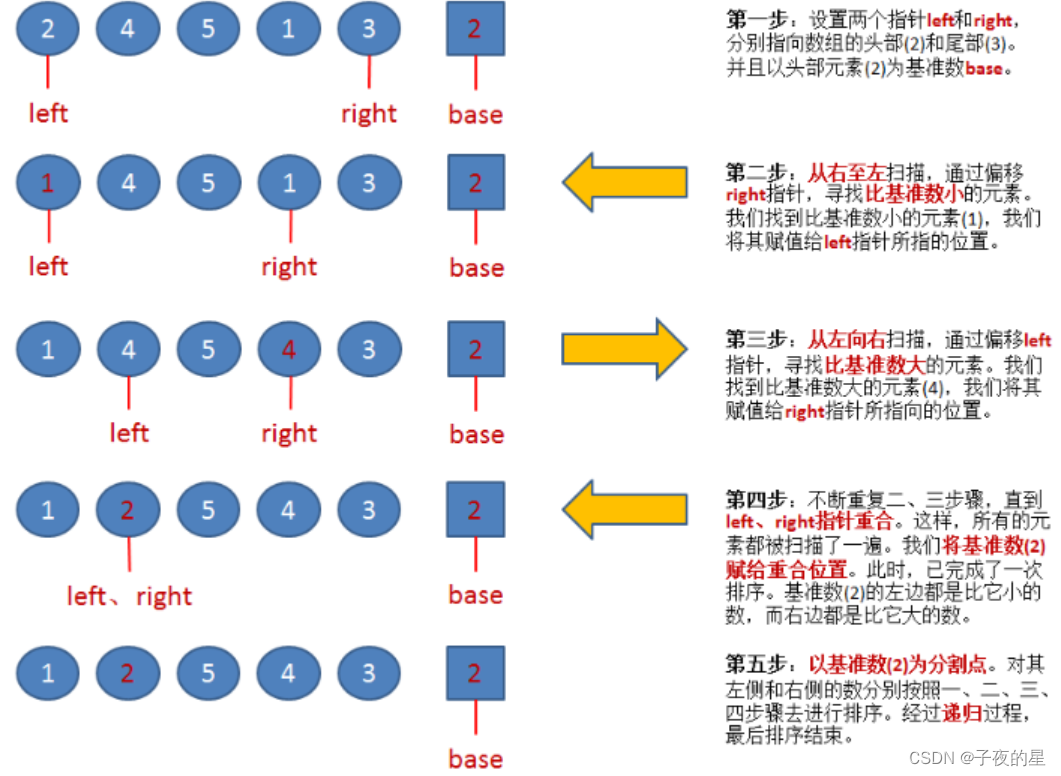
2.动图分析

3.代码模板

//递归实现快速排序
void quick_sort(int q[], int l, int r)
{
    if (l >= r) return;
    int i = l - 1, j = r + 1, x = q[l + r >> 1];
    while (i < j)
    {
        do i++; while (q[i] < x);
        do j--; while (q[j] > x);
        if (i < j)
        {
           //交换数据
            int tmp;
            tmp = q[i];
            q[i] = q[j];
            q[j] = tmp;
        }
    }
    //递归处理左右两段
    quick_sort(q, l, j), quick_sort(q, j + 1, r);
}