| 文中代码源文件已上传:数据结构源码 <-上一篇 初级数据结构(六)——堆 | NULL 下一篇-> |
1、写在前面
二叉树的基本概念在《初级数据结构(五)——树和二叉树的概念》中已经介绍得足够详细了。上一篇也演示了利用顺序表模拟二叉树。但链表形式的二叉树在逻辑上相对于顺序表尤其复杂,当然也比顺序表更为灵活。
链表形式的二叉树任何操作,本质都是有条件地遍历各个节点。而熟练掌握递归算法对遍历链表形式二叉树尤为重要。如果你对递归还犯迷糊可先翻阅《轻松搞懂递归算法》一文,其中对递归有较为详细的介绍。
2、建立
链表形式的二叉树的创建操作已经属于遍历操作了,本部分将通过边创建边说明的方式演示如何遍历二叉树。
2.1、前期工作
老样子,先建文件。

binaryTree.h :用于创建项目的结构体类型以及声明函数;
binaryTree.c :用于创建二叉树各种操作功能的函数;
main.c :仅创建 main 函数,用作测试。
这次演示是通过字符串创建二叉树,空节点以“ ? ”表示,所以在 binaryTree.h 中先写下如下代码:
#include <stdio.h>
#include <stdlib.h>
typedef char DATATYPE;
#define NULL_SYMBOL '?'
#define DATA_END '\0'
#define DATAPRT "%c"
//创建二叉树节点
typedef struct Node
{
DATATYPE data;
struct Node* left;
struct Node* right;
}Node;
//函数声明-------------------------------------
//创建二叉树
extern Node* BinaryTreeCreate(DATATYPE*);
//销毁二叉树
extern void BinaryTreeDestroy(Node*);然后在 binaryTree.c 中 include 一下:
#include "binaryTree.h"在 main.c 中创建个 main 函数的空客:
#include "binaryTree.h"
int main()
{
return 0;
}2.2、常规遍历
二叉树有三种常用遍历顺序,称为前序、中序和后序。前中后序指的是访问节点中数据的次序。
前序:先访问根节点,之后问左树,最后访问右树。
中序:先访问左树,之后问根节点,最后访问右树。
后序:先访问左树,之后问右树,最后访问根节点。
先看图:

用前序访问上图第一棵树顺序是 A→B→C ,中序是 B→A→C ,后序则是 B→C→A 。而这是相对于子树而言的。如果访问上图第二棵树需要将树根据当前访问的节点拆分为子树。如用前序访问,先访问 D ,之后定位到 D 的左节子点 E , 但此时是先将 E 节点当作子树,访问的是该子树的根节点。 之后访问 G 也是如此。用前序访问的顺序是 D→E→G→F→H→I 。而实际访问顺序如下图:

D→E→G→NULL→NULL→NULL→F→H→NULL→NULL→I→NULL→NULL 。
用前序来说明可能不太明显。如果用中序,先定位到 D 节点,此时先不访问 D 的数据,而是访问 D 的左子节点 E 。而 E 作为子树,它还存在自己的左子节点,因此也不访问 E 的数据,而是它的子节点 G 。此时以 G 为根节点的子树不存在左子节点,因此访问 G 的数据,然后访问 G 的右子节点。但 G 不存在右子节点,所以访问完 G 的数据也就是访问完以 G 为根节点的子树,相当于 E 的左树访问完毕,此时才访问 E 的数据。下一步访问 E 的右子节点,但 E 不存在右子节点,所以 以 E 为根的子树访问完成,相当于 D 的左子树访问完毕,所以访问 D 的数据,然后访问 D 的右子树 F ……因此,以中序访问这棵树顺序是 G→E→D→H→F→I 。实际访问顺序:
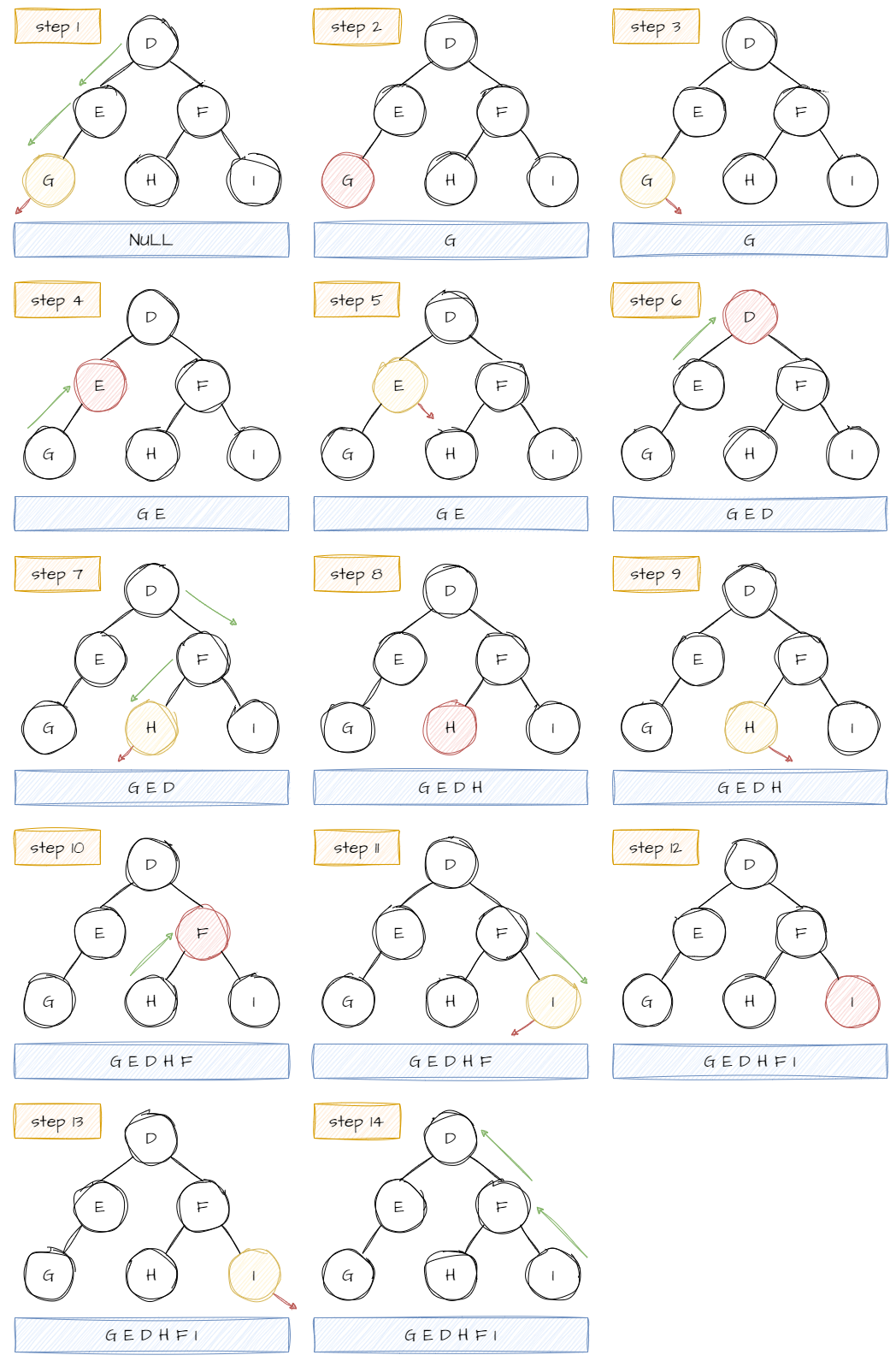
NULL→G→NULL→E→NULL→D→H→NULL→NULL→F→I→NULL→NULL 。
后序的逻辑可以类比中序,访问顺序是 G→E→H→I→F→D 。实际访问顺序:

NULL→NULL→G→NULL→E→NULL→NULL→H→NULL→NULL→I→F→D 。
2.3、操作函数
2.3.1、创建二叉树
创建二叉树的过程也是在遍历二叉树。而创建过程中,必须先有根节点,才能创建子树,所以建立二叉树是以前序边创建边访问建立的。
需要解决的问题是在创建节点的结构体时,并没有创建指向父节点的指针成员变量。当创建完左树之后,要如何回到根节点。这里先往回思考,在前中后序的说明中不难看出,这就是一种递归。树拆成子树,子树又拆成子树的子树……而不论拆分成哪一级子树,访问方式都是统一的顺序。而递归是具有回溯属性的,也就是说,用递归的方式创建二叉树再合适不过了。函数的代码便呼之欲出:
//创建二叉树
Node* BinaryTreeCreate(DATATYPE** ptr2_data)
{
//参数有效性判定
if (!ptr2_data || !*ptr2_data)
{
fprintf(stderr, "Data Address NULL\n");
return NULL;
}
//数据为空节点符号或末位尾符号则返回
if (**ptr2_data == NULL_SYMBOL || **ptr2_data == DATA_END)
{
return NULL;
}
//创建节点
Node* node = NULL;
while (!node)
{
node = (Node*)malloc(sizeof(Node));
}
//前序递归
node->data = **ptr2_data;
*ptr2_data += !(**ptr2_data == DATA_END);
node->left = BinaryTreeCreate(ptr2_data);
*ptr2_data += !(**ptr2_data == DATA_END);
node->right = BinaryTreeCreate(ptr2_data);
return node;
}在 main 函数中用以下代码进行测试:
DATATYPE data[] = "abc??d??f?g?h";
DATATYPE* ptr_data = data;
Node* root = BinaryTreeCreate(&ptr_data);树并不像线性表那么直观,检查测试结果时最好自己先画图,然后在监视窗口中检查。对于以上测试结果应当如下图:

调试起来,将调试窗口中逐层展开,对其中的信息对比上图。或者另外画图, 将两张图作对比进行检查。

结果正确。顺带写出前中后三种顺序访问二叉树的函数。这里为了方便观察遍历顺序,多加一个参数用于控制是否显示空节点。先在 binaryTree.h 中加个枚举类型以完善传参时代码的可读性:
enum NULL_VISIBLE
{
HIDE_NULL, //空节点不可见 = 0
SHOW_NULL //空节点可见 = 1
};然后加声明:
//前序访问二叉树
extern void PreOrderTraversal(Node*, int);
//中序访问二叉树
extern void InOrderTraversal(Node*, int);
//后序访问二叉树
extern void PostOrderTraversal(Node*, int);函数具体内容:
//前序访问二叉树
void PreOrderTraversal(Node* root, int NULLvisible)
{
//空树返回
if (!root)
{
if (NULLvisible == SHOW_NULL)
{
printf("NULL ");
}
return;
}
printf(DATAPRT" ", root->data);
PreOrderTraversal(root->left, NULLvisible);
PreOrderTraversal(root->right, NULLvisible);
}
//中序访问二叉树
void InOrderTraversal(Node* root, int NULLvisible)
{
//空树返回
if (!root)
{
if (NULLvisible == SHOW_NULL)
{
printf("NULL ");
}
return;
}
InOrderTraversal(root->left, NULLvisible);
printf(DATAPRT" ", root->data);
InOrderTraversal(root->right, NULLvisible);
}
//后序访问二叉树
void PostOrderTraversal(Node* root, int NULLvisible)
{
//空树返回
if (!root)
{
if (NULLvisible == SHOW_NULL)
{
printf("NULL ");
}
return;
}
PostOrderTraversal(root->left, NULLvisible);
PostOrderTraversal(root->right, NULLvisible);
printf(DATAPRT" ", root->data);
}这里可以观察到,所谓前中后序不过是调整了一下访问 root->data 语句的位置,其余完全一样。
然后开始测试。
int main()
{
DATATYPE data[] = "abc??d??f?g?h";
DATATYPE* ptr_data = data;
Node* root = BinaryTreeCreate(&ptr_data);
//前序:
printf("前序 --------------------\n");
PreOrderTraversal(root, SHOW_NULL);
printf("\n");
PreOrderTraversal(root, HIDE_NULL);
printf("\n");
//中序
printf("中序 --------------------\n");
InOrderTraversal(root, SHOW_NULL);
printf("\n");
InOrderTraversal(root, HIDE_NULL);
printf("\n");
//后序
printf("后序 --------------------\n");
PostOrderTraversal(root, SHOW_NULL);
printf("\n");
PostOrderTraversal(root, HIDE_NULL);
printf("\n");
return 0;
}
对比上面的图,说明代码正确。
2.3.2、销毁二叉树
销毁跟创建是同样的逻辑,必须从底层开始销毁。当然也可以从根部销毁,但如果不先销毁子节点,一旦销毁根节点之后便无法再找到子节点的地址,因此还得对子节点地址进行记录后再销毁,显得过于麻烦。因此采用后序遍历销毁最为简便。
//销毁二叉树
void BinaryTreeDestroy(Node* root)
{
//空树直接返回
if (!root) return;
//后序递归销毁节点
BinaryTreeDestroy(root->left);
BinaryTreeDestroy(root->right);
free(root);
}这个函数测试过程需要一步一步调试观察。 实际上跟之前后序访问的函数是一个道理,这里也没必要再多作测试。但使用完该函数记得把根节点指针置空。
2.3.3、搜索
搜索也是通过遍历比对节点中的数据,再返回节点地址。
必不可少的声明:
//二叉树搜索
extern Node* BinaryTreeSearch(Node*, DATATYPE);代码:
//二叉树搜索
Node* BinaryTreeSearch(Node* root, DATATYPE data)
{
//空树直接返回
if (!root) return NULL;
//创建节点地址指针
Node* node = NULL;
//前序搜索
node = (root->data == data ? root : NULL);
node = (node ? node : BinaryTreeSearch(root->left, data));
node = (node ? node : BinaryTreeSearch(root->right, data));
return node;
}在刚才创建的二叉树基础上测试:
Node* node = NULL;
node = BinaryTreeSearch(root, 'f');
if (node)
printf("Found Data '"DATAPRT"' In 0x%p\n", node->data, node);
else
printf("Not Found\n");
node = BinaryTreeSearch(root, 'j');
if (node)
printf("Found Data '"DATAPRT"' In %p\n", node->data, node);
else
printf("Not Found\n");
测试通过。此外,搜索既然实现了,修改就不必说了,这里不再演示。
3、层序
除了之前提到的前中后序遍历二叉树以外,还有层序遍历。顾名思义,就是逐层遍历二叉树中每个节点。层序遍历是最复杂的一种遍历方式。由于二叉树节点中并不包含兄弟节点和堂兄弟节点的指针,因此层序遍历需要其他变量来记录各层节点的左右子节点,并按照一定顺序排序。
3.1、队列
这里可以利用队列的特性,访问完根节点后,对左右子节点地址进行入队,并将根节点出队,从而实现遍历。因此,这里先在 binaryTree.h 中创建个队列。
//队列类型
typedef struct Queue
{
int top;
int bottom;
size_t capacity;
Node* data[];
}Queue;之后是在 binaryTree.c 中创建操作队列的各个函数。
//创建队列并初始化
static Queue* QueueCreate()
{
Queue* queue = NULL;
//创建队列
while (!queue)
{
queue = (Queue*)malloc(sizeof(Queue) + sizeof(Node*) * 4);
}
queue->top = -1;
queue->bottom = -1;
queue->capacity = 4;
//返回队列
return queue;
}
//数据入队
static void QueuePush(Queue** queue, Node* node)
{
//若队列空间不足,扩容
if ((*queue)->top + 1 >= (*queue)->capacity)
{
Queue* tempQueue = NULL;
while (!tempQueue)
{
tempQueue = (Queue*)realloc(*queue, sizeof(Queue) + sizeof(Node*) * (*queue)->capacity * 2);
}
(*queue) = tempQueue;
(*queue)->capacity *= 2;
}
//节点入队
(*queue)->bottom = ((*queue)->bottom == -1 ? 0 : (*queue)->bottom);
(*queue)->top++;
(*queue)->data[(*queue)->top] = node;
}
//数据出队
static void QueuePop(Queue* queue)
{
//空队列返回
if (queue->top == -1)return;
//出队
queue->bottom++;
//出队后若为空队列
if (queue->bottom > queue->top)
{
queue->bottom = -1;
queue->top = -1;
}
}3.2、层序访问
由于二叉树是有序树,每一层节点从左到右必然是有序的。仍以这棵树作演示:

首先将根节点 D 入队,访问完根节点后,将左右子节点 E、F 依次入队,排在 D 之后,然后弹出 D 。之后访问 E,再将 E 的左右子节点 G 和 NULL 入队,弹出 E 。继续访问 F ,H、I 入队后再弹出 F 。如果当前根节点为 NULL ,则不再将子节点入队,仅仅弹出 NULL 。最后当队列为空时,树也遍历完毕。
根据以上描述,可以知道层序访问顺序为 D→E→F→G→H→I,实际访问顺序:

D→E→F→G→NULL→H→I→NULL→NULL→NULL→NULL→NULL→NULL 。
3.3、代码部分
思路已经有了,代码也就顺理成章了。
//层序打印
static void LevelOrderPrint(Queue** queue)
{
//空队列返回
if ((*queue)->top == -1) return;
//非空节点的左右子节点入队
if ((*queue)->data[(*queue)->bottom])
{
QueuePush(queue, ((*queue)->data[(*queue)->bottom])->left);
QueuePush(queue, ((*queue)->data[(*queue)->bottom])->right);
}
//打印非空节点
if ((*queue)->data[(*queue)->bottom] != NULL)
{
printf(DATAPRT" ", ((*queue)->data[(*queue)->bottom])->data);
}
//根节点出队
QueuePop(*queue);
LevelOrderPrint(queue);
}
//层序遍历二叉树
void LevelOrderTraversal(Node* root)
{
//创建队列
Queue* queue = QueueCreate();
//根节点入队
QueuePush(&queue, root);
//层序打印
LevelOrderPrint(&queue);
//销毁队列
free(queue);
}仍沿用开头的测试案例,然后在 main 函数最后加入以下语句进行测试:
//层序
printf("层序 --------------------\n");
LevelOrderTraversal(root);
printf("\n");![]()
至此完成。