1.题目

#include<stdio.h>
int main()
{
 int arr[]={1,2,3,4,5};
 short*p = (short*)arr;
 int i = 0;
 for(i=0;i<4;i++)
 {*(p+i)=0;}
 for(i=0;i<5;i++)
 {printf("%d ",arr[i];}
 return 0;
}
 

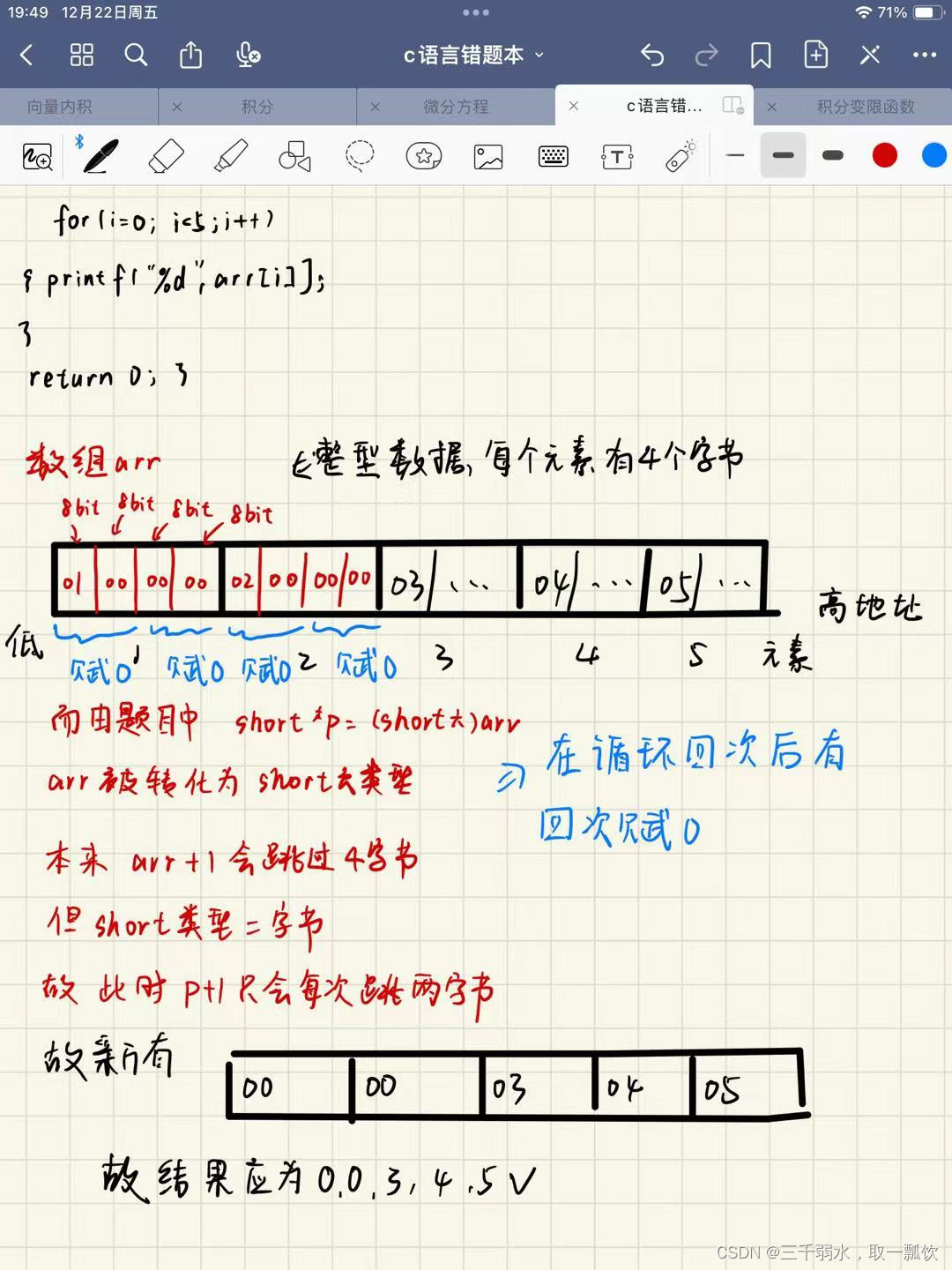
2.解析

  这道题主要容易错在，大家会以为通过指针赋值的时候，会将数组中的四个元素均赋值为0，从而我们得到0 0 0 0 5的答案，但其实不然，我们最后得到的结果实际上是0 0 3 4 5，这是因为我们在给指针初始化的时候，给指针类型为short*类型，这导致我们在进行指针的加法的时候，它就只会跳过2个字节，具体的变化形式，以及分析的过程，我将通过图像结合文字来呈现：