经典解法，创建K个大小的堆

传统的直接建立一个K个元素的小顶堆，类似堆排序的思想， 然后将剩下的n-k个元素依次和堆顶元素比较，如果大于堆顶，就替换掉堆顶，然后向下调整到合适的位置，以此类推，最后这个堆中剩下的K个元素就是topK元素; 时间O (n logk) 空间O(k) ;相对来说是比较优的;

不考虑空间的暴力排序做法

1. 归并等排序…时间O(NlogN) O(N)

2. 时间上更优O(N): 类似于计数排序的映射思想，直接创建一个存的下所有int数字的数组，全按照原数据下标的index位置映射存进一个数组，出现一次数组的内容cnt++一次，之后从数组的末尾开始，从后往前遍历(topK)出来k个数字即可; 时间O(n)空间O(n); 是更快了一点哈; 但是这样有点太暴力了…

不考虑空间的快排partition变形减治法思想(核心：找第K大的数)

这里的减治法与分治法的区别(抽象举例):

处理元素以这个序列为例：111 2 333

• 分治法: 假设以2为基准，我们把序列分为了111 和 333两部分，进而对这两部分继续按照一定的规则分治处理;

• 减治法：假设以2为基准，我们找的是第3大的数，那么111直接被丢弃，我们只需要对333进一步减治处理即可，与分治法比较，省去了对排除部分进行分支处理的开销！

思路:

1. 找到第K大的数字（借助快排的partion思想返回的pos区分左右两个侧大小的下标和二分的减治思想！注意:有重复也不影响哦; 前k大的数字 可以有多个一样的呀！）

2. 然后再利用这个数字进行一次快排的partition，通过返回的下标，区分左右两侧，就能确定topK的数字了;

注意下图是找到第K小的数字(第k大还是小，取决于我们partition左侧方的是>=基准值得数还是<=基准值的数)

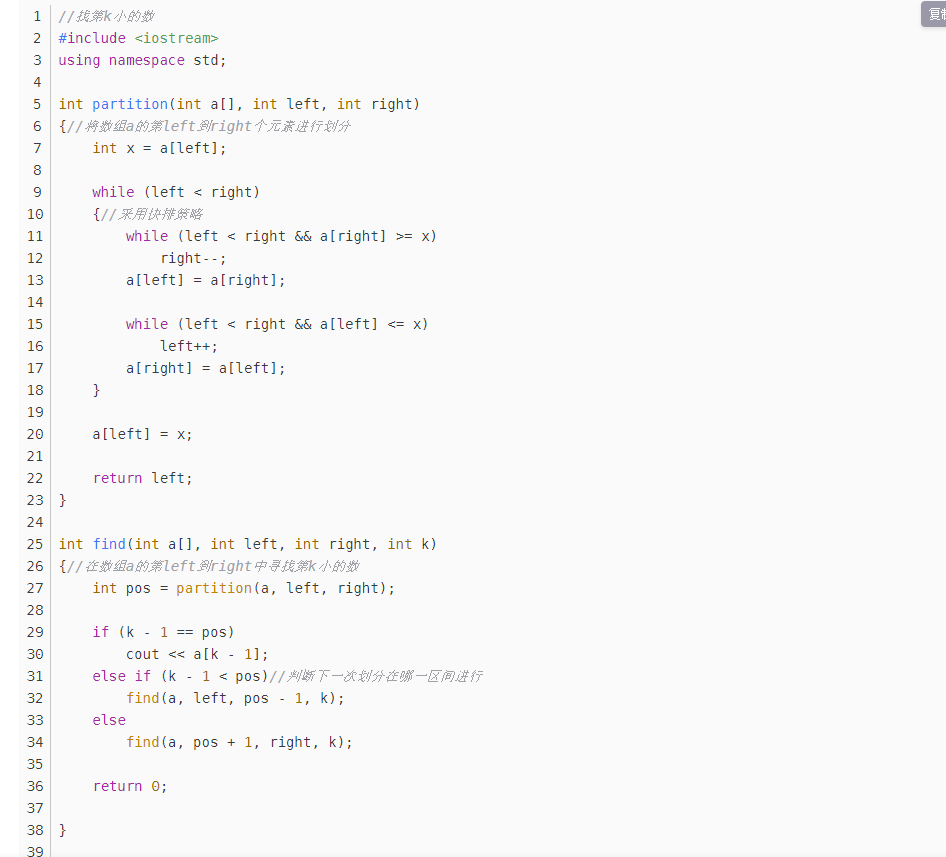
找到第K大的数字以后; 进行一次partion，>=他的放在右边，那么右边就是前K大的了;

(同理，前k小，就找第k小，一次partion左边都是<= 的前k小了)

我们只在一段序列中partion出对应第k大的数字位置的下标即可，其他淘汰的字段不用再partion了，这种方法就避免了对除了Top K个元素以外的数据进行排序所带来的不必要的开销。

空间有限放不下，海量数据的分治法

将全部数据等分成N份，（N份前提是每份的数据都可以读到内存中进行处理），找到每份数据中最大的K个数;

再把这一共：N*K个（N份*每份的K个）的数据放入内存处理，可以用快排变形或者归并排序等;

（注意：如果N*K个如果又放不下，那么以此类推，继续分治，拿N*K个数据等分成每份M份（M份前提是放的进内存的粒度），再找topK，再把M*K个合起来放入内存用快排变形或者排序处理，以此类推;