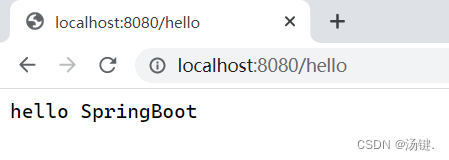
引言
这是中科大最优化理论的笔记,中科大凌青老师的凸优化课程,详尽易懂,基础扎实。不论是初学者还是从业多年的人,都值得系统地好好学一遍。
本文主要介绍什么是凸优化,通过几个例子来阐述什么是凸优化问题。让大家有一个感性的认知。
优化/数学规划
优化(Optimization)或称为数学规划(Mathematical Programming)是从一个可行解的集合中,寻找出最优的元素。
任何一个优化问题,可以写成下面这样的形式:
minimize
f
0
(
x
)
subject to
f
i
(
x
)
≤
b
i
,
i
=
1
,
…
,
m
(1)
\begin{aligned} \text{minimize}\ &f_0(x)\\ \text{subject to}\ &f_i(x)\leq b_i,\ \ \ i=1,\dots,m\\ \end{aligned} \tag{1}
minimize subject to f0(x)fi(x)≤bi, i=1,…,m(1)
我们要最小化
f
0
(
x
)
f_0(x)
f0(x),同时有一些约束,使得
f
i
(
x
)
≤
b
i
f_i(x) \leq b_i
fi(x)≤bi,总共有
m
m
m个约束。
这里 x x x一般来说是一个 n n n维的向量, x = [ x 1 , ⋯ , x n ] T x=[x_1,\cdots,x_n]^T x=[x1,⋯,xn]T,称为优化变量(ptimization variable);
函数 f 0 : R n → R f_0: R^n \rightarrow R f0:Rn→R,称为目标函数(objective function),是一个从 n n n维到 1 1 1维的映射。
函数 f i : R n → R , i = 1 , ⋯ , m f_i:R^n \rightarrow R, i=1,\cdots,m fi:Rn→R,i=1,⋯,m 为不等式约束(inequality constraint)函数,而一个等式约束可以写成两个不等式约束,这里为了简便,就不写出等式约束了;
优化问题的解,最优的 x x x记为 x ∗ x^* x∗,等价于 ∀ z ∈ R n \forall z \in R^n ∀z∈Rn,对于 z ∈ { f i ( z ) ≤ b i , i = 1 , ⋯ , m } z \in \{f_i(z) \leq b_i, i=1,\cdots,m \} z∈{fi(z)≤bi,i=1,⋯,m},总是有 f 0 ( z ) ≥ f 0 ( x ∗ ) f_0(z) \geq f_0(x^*) f0(z)≥f0(x∗),即对于所有满足约束条件的 z z z,其结果都不会好于最优解。
集合 { f i ( z ) ≤ b i , i = 1 , ⋯ , m } \{f_i(z) \leq b_i, i=1,\cdots,m \} {fi(z)≤bi,i=1,⋯,m}是可行解集合(feasible set),即所有满足约束点的集合。
这里描述的是一般的优化问题,任何一般的优化问题都可以写成这样的形式。
这里的数学公式优点抽象,下面我们来看一些优化问题的例子。
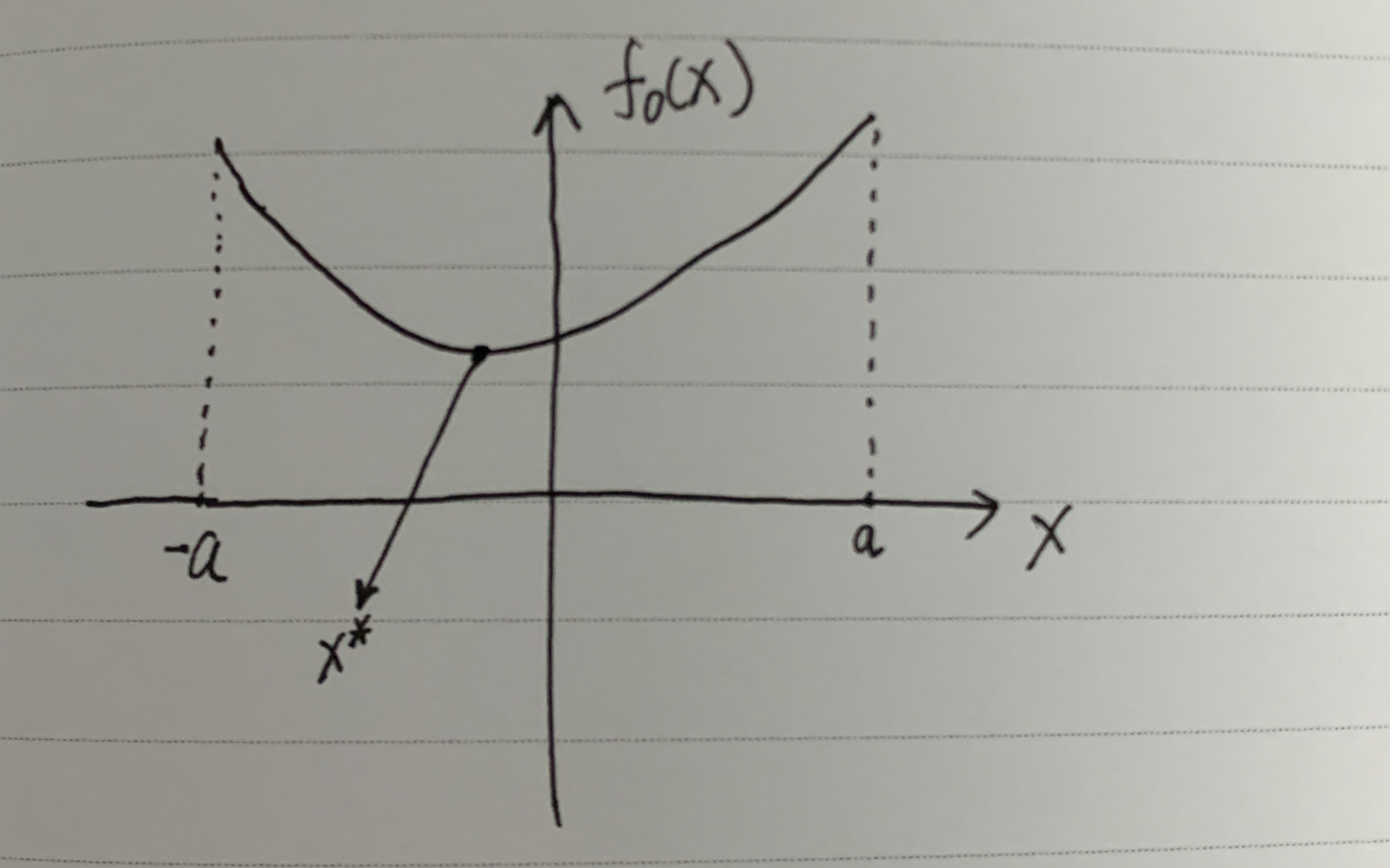
如上图,假设我们要优化这样一个目标函数,约束是:
x
≤
a
−
x
≤
a
x \leq a \\ -x \leq a
x≤a−x≤a
相当于
x
∈
[
−
a
,
a
]
x \in [-a,a]
x∈[−a,a]之间,可行解集为
−
a
-a
−a到
a
a
a之间所有的点所构成的点集。最优解是在上图
x
∗
x^*
x∗处。
如果我们把该曲线改一下:
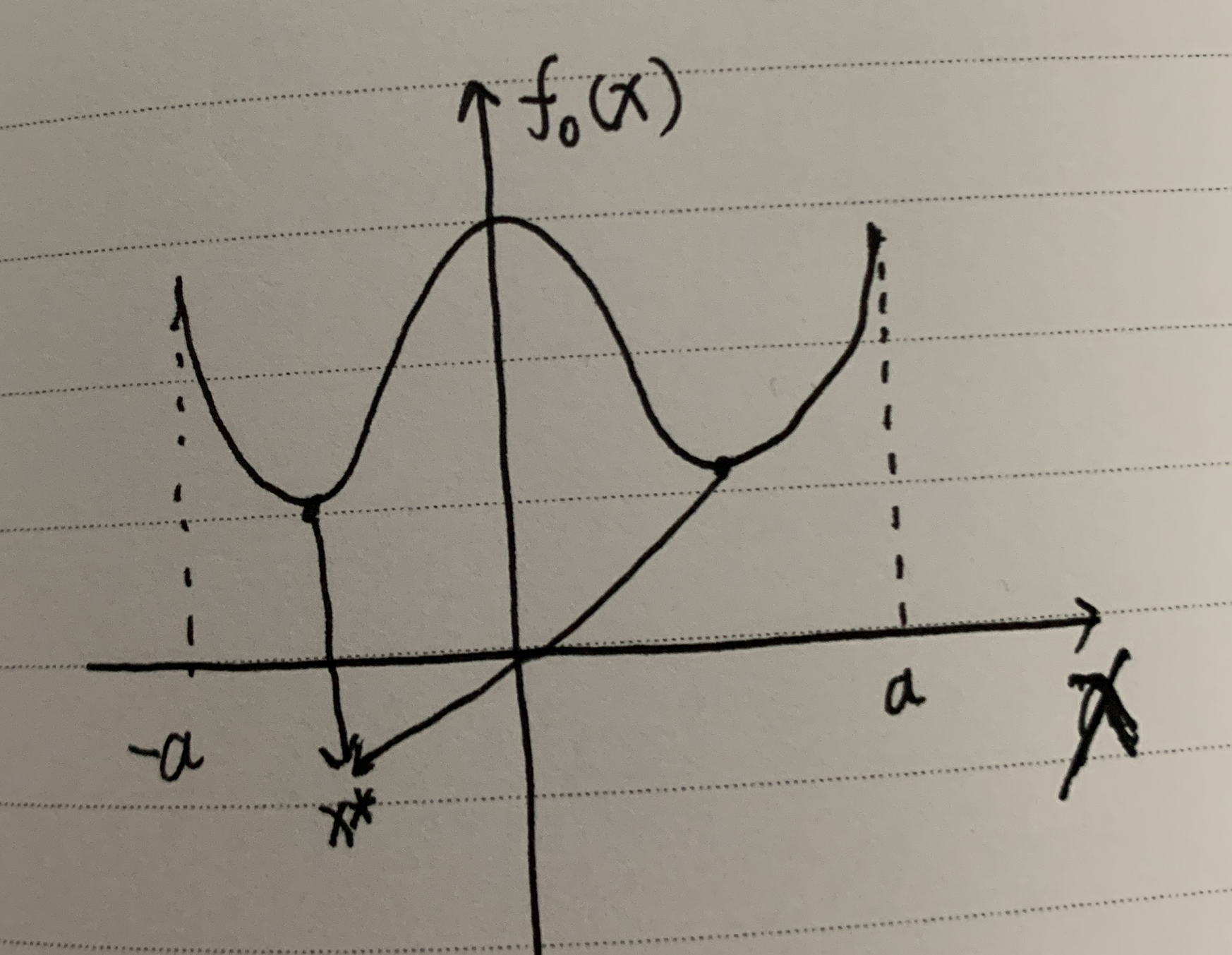
同样于 x ∈ [ − a , a ] x \in [-a,a] x∈[−a,a]之间,这个问题看起来有两个最优解,没错,该问题的最优解集是由这两个点所构成的集合。
所以最优解并不一定只有一个,一般只有一个最优解的问题会简单一点。
应用
本小节介绍几个例子。
数据拟合问题
假设我们通过一个实验得到一些散点,我们想把这些散点拟合成一条线。
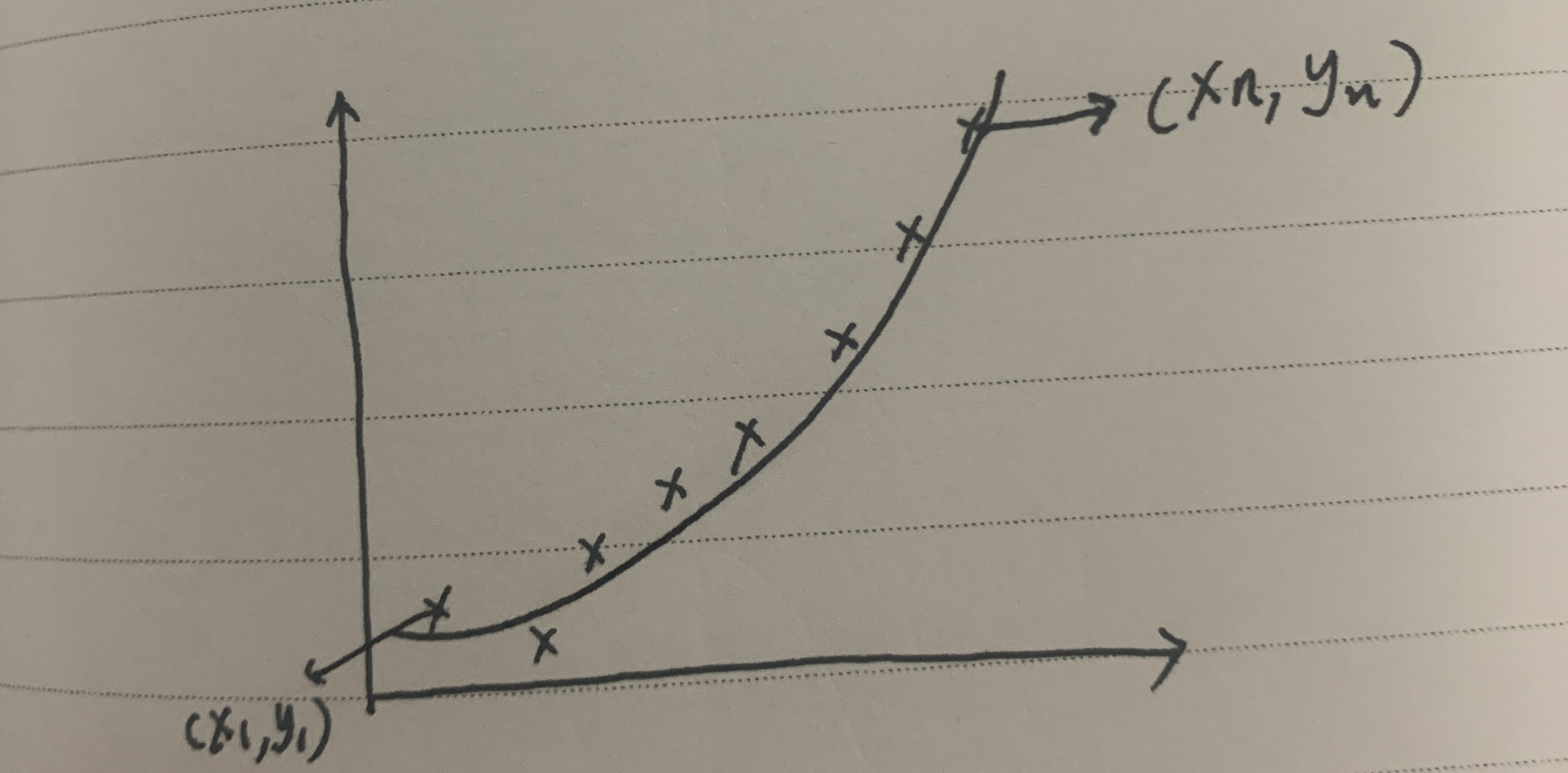
如上图,现在有 ( x 1 , y 1 ) , ⋯ , ( x n , y n ) (x_1,y_1),\cdots,(x_n,y_n) (x1,y1),⋯,(xn,yn)这些点,假设这条线是一个二次曲线。
可以写成: y = a x 2 + b x + c y=ax^2 + bx+c y=ax2+bx+c
其中 x , y x,y x,y可以通过测量知道,而 a , b , c a,b,c a,b,c是需要估计的参数。
而测量是有误差的,我们目标是使得测量误差尽可能小,所以用最小二乘准则
min
ϵ
1
2
+
ϵ
2
2
+
⋯
+
ϵ
n
2
\min \quad \epsilon_1^2 + \epsilon_2^2 + \cdots + \epsilon_n^2
minϵ12+ϵ22+⋯+ϵn2
其中
ϵ
i
=
y
i
−
(
a
x
i
2
+
b
x
i
+
c
)
,
i
=
1
,
⋯
,
n
\epsilon_i = y_i - (ax_i^2 + bx_i +c), \quad i=1,\cdots ,n
ϵi=yi−(axi2+bxi+c),i=1,⋯,n
即,我们要使所有测量误差的平方和尽可能的小,这就是一个最小二乘问题。这是一个很典型的优化问题。
图像处理
假设给定一个二维图像 Φ 0 ( x , y ) \Phi_0(x,y) Φ0(x,y),且该图像是带噪声的,希望恢复出一个不带噪声的图像 Φ ( x , y ) \Phi(x,y) Φ(x,y)。
其中 x , y x,y x,y两个坐标轴。
我们知道所有的图像都是有一定的规律,图像具有分片光滑性,即图片中通常具有很大的色块。这些色块为我们提供了先验知识,使得图像的TV范数尽可能小。
TV范数(Total Variation)表示的意义是使图像分片光滑的,可以定义如下:
∣
∣
Φ
∣
∣
T
V
=
∑
y
∑
x
(
Φ
(
x
,
y
)
−
Φ
(
x
,
y
−
1
)
)
2
+
(
Φ
(
x
,
y
)
−
Φ
(
x
−
1
,
y
−
1
)
)
2
||\Phi||_{TV} = \sum_y\sum_x \sqrt{(\Phi(x,y)-\Phi(x,y-1))^2 + (\Phi(x,y)-\Phi(x-1,y-1))^2}
∣∣Φ∣∣TV=y∑x∑(Φ(x,y)−Φ(x,y−1))2+(Φ(x,y)−Φ(x−1,y−1))2
表示对图像做两个方向上的差分,然后计算平方,再求和,最后取根号。
对于任何一个分片光滑的图像,它的TV范数一定都是比较小的。有了这样一个先验知识后,我们就可以写出这样一个优化问题:
min
Φ
∣
∣
Φ
∣
∣
T
V
+
λ
∣
∣
Φ
−
Φ
0
∣
∣
F
2
\min_\Phi \quad ||\Phi||_{TV} + \lambda ||\Phi - \Phi_0||_F^2
Φmin∣∣Φ∣∣TV+λ∣∣Φ−Φ0∣∣F2
我们要找到一个这样的
Φ
\Phi
Φ,它的TV范数要尽可能的小,实际上就是一个分片光滑的图片。上式后面那一项是规范化项,因为我们要求
Φ
\Phi
Φ不光是分片光滑的,还希望
Φ
\Phi
Φ与
Φ
0
\Phi_0
Φ0比较接近。即这两个矩阵之差的F范数要尽可能的小。
这个模型就是图像中非常著名的TV-L2模型。
优化问题的分类
优化问题按照不同的角度可以分成哪些类呢?
线性规划/非线性规划
线性规划就是说,优化问题的目标函数和所有的约束函数均为线性函数。
那什么是线性函数?
若某数学函数或数量关系的函数图像呈现一条直线或线段,那么这种关系就是一种线性的关系,该函数称为线性函数。
在线性代数中,线性函数时一个线性映射,是在两个向量空间之间,维持向量加法与标量乘法的映射。
f
(
a
+
b
)
=
f
(
a
)
+
f
(
b
)
f
(
k
a
)
=
k
f
(
a
)
\begin{aligned} f(a + b) &= f(a) + f(b) \\ f(ka) &= kf(a) \end{aligned}
f(a+b)f(ka)=f(a)+f(b)=kf(a)
回到凸优化中,线性规划的函数满足
f
i
(
α
x
+
β
y
)
=
α
f
i
(
x
)
+
β
f
i
(
y
)
i
=
0
,
1
,
⋯
,
m
f_i(\alpha x + \beta y) = \alpha f_i(x) + \beta f_i(y) \quad i=0,1,\cdots,m
fi(αx+βy)=αfi(x)+βfi(y)i=0,1,⋯,m
对于一个优化问题,它的这些函数都是线性函数的化,那么这个问题就是线性规划问题。
对于线性规划问题,可能以如下图像表示。
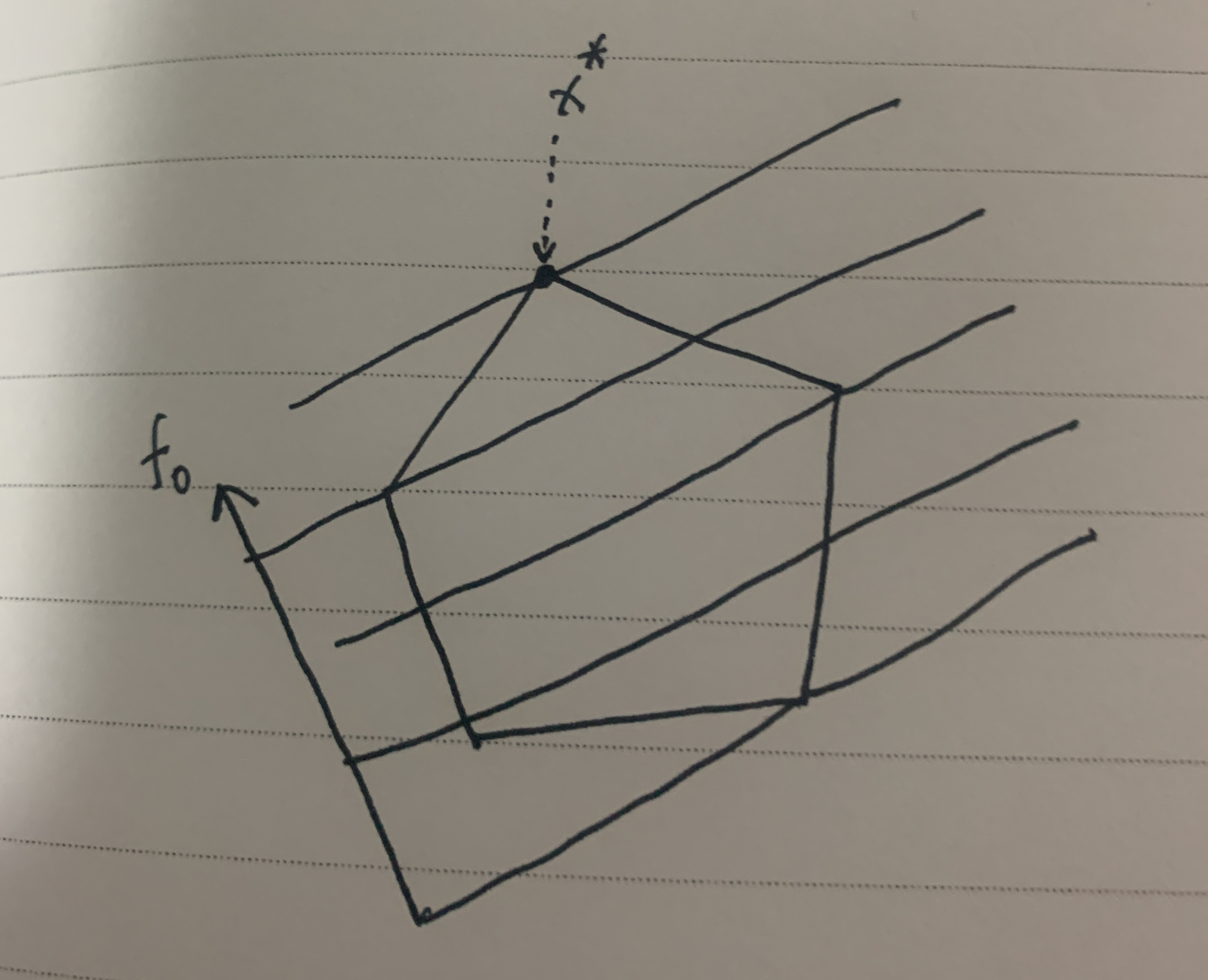
该图表示线性规划问题中约束所构成的空间,这里是一个五边形。
目标函数也是线性函数,我们可以在该空间中画一些等高线,每条线表示对应 f 0 f_0 f0的取值,等高线上的 f 0 f_0 f0取值相等。上图箭头所指的方向为 f 0 f_0 f0下降的方向。任何一个线性规划问题的最优解一定是在顶点上或边上。
这里最优解为 x ∗ x^* x∗的位置。
如果存在一个或多个 f i f_i fi是非线性函数,那么该问题就是非线性规划问题。
凸规划/非凸规划
对于所有
f
i
f_i
fi都为凸函数,有
f
i
(
α
x
+
β
y
)
≤
α
f
i
(
x
)
+
β
f
i
(
y
)
i
=
0
,
1
,
⋯
,
m
f_i(\alpha x + \beta y) \leq \alpha f_i(x) + \beta f_i(y) \quad i=0,1,\cdots,m
fi(αx+βy)≤αfi(x)+βfi(y)i=0,1,⋯,m
或者说它的可行解集是凸集且目标函数是凸函数。
下面来举个例子看下什么叫凸函数,什么叫非凸函数。
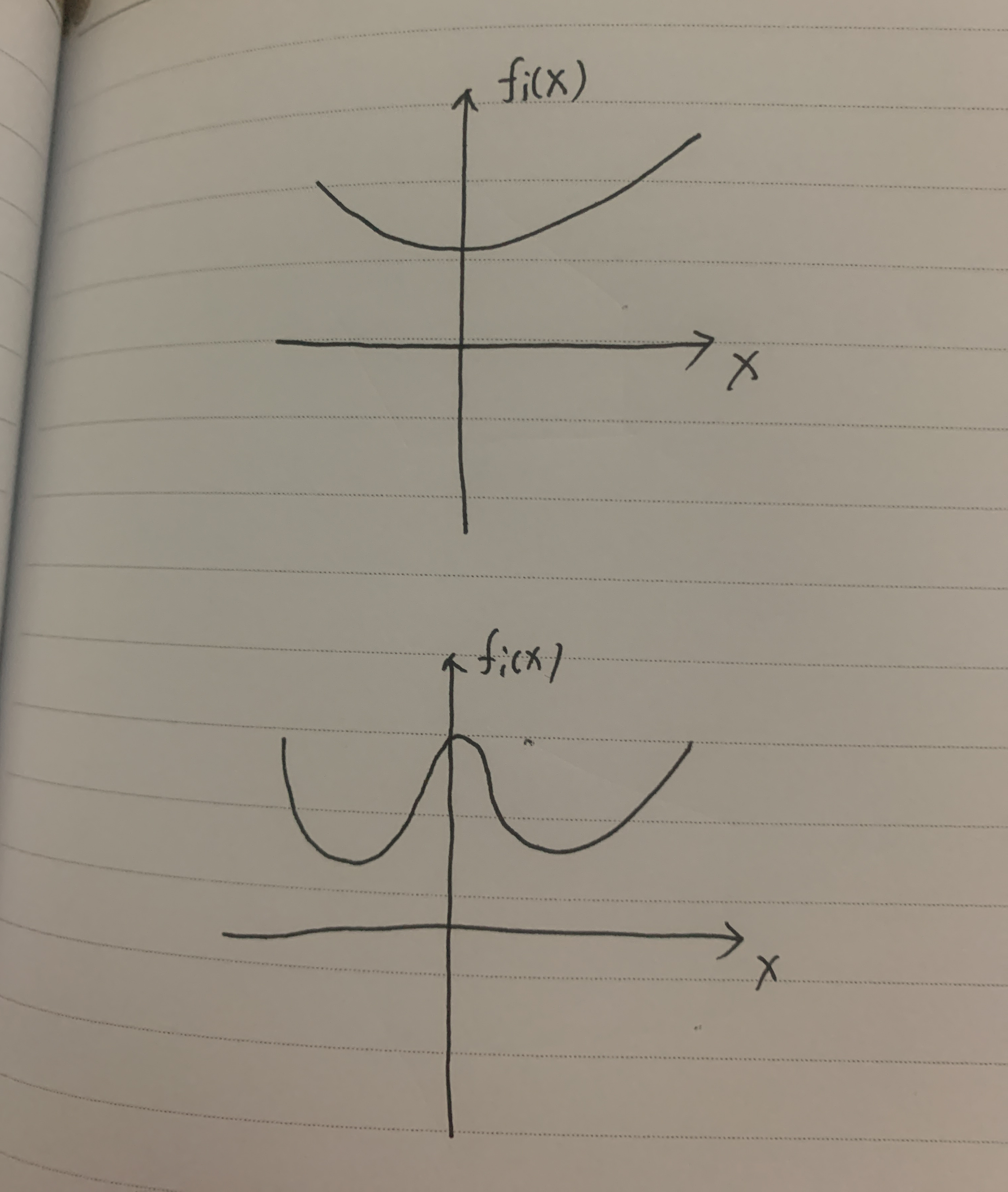
上图中上半区域的图像代表凸函数,下半区域的图像表示非凸函数。
在凸函数中无法找到一些不相邻的最低的点;而非凸函数能找到不相邻的比较低的点。
为什么要分凸规划(凸优化)和非凸规划,因为凸规划问题是容易解决的优化问题,而非凸规划问题是难解决的优化问题。
任何一个线性规划问题都是凸规划问题。
光滑/非光滑
光滑和非光滑一般针对目标函数 f 0 ( x ) f_0(x) f0(x)而言的,如果一个函数 f 0 ( x ) f_0(x) f0(x)是光滑的,即它在每个点上都是可微的。
如下图:

如果一个目标函数是非光滑的:
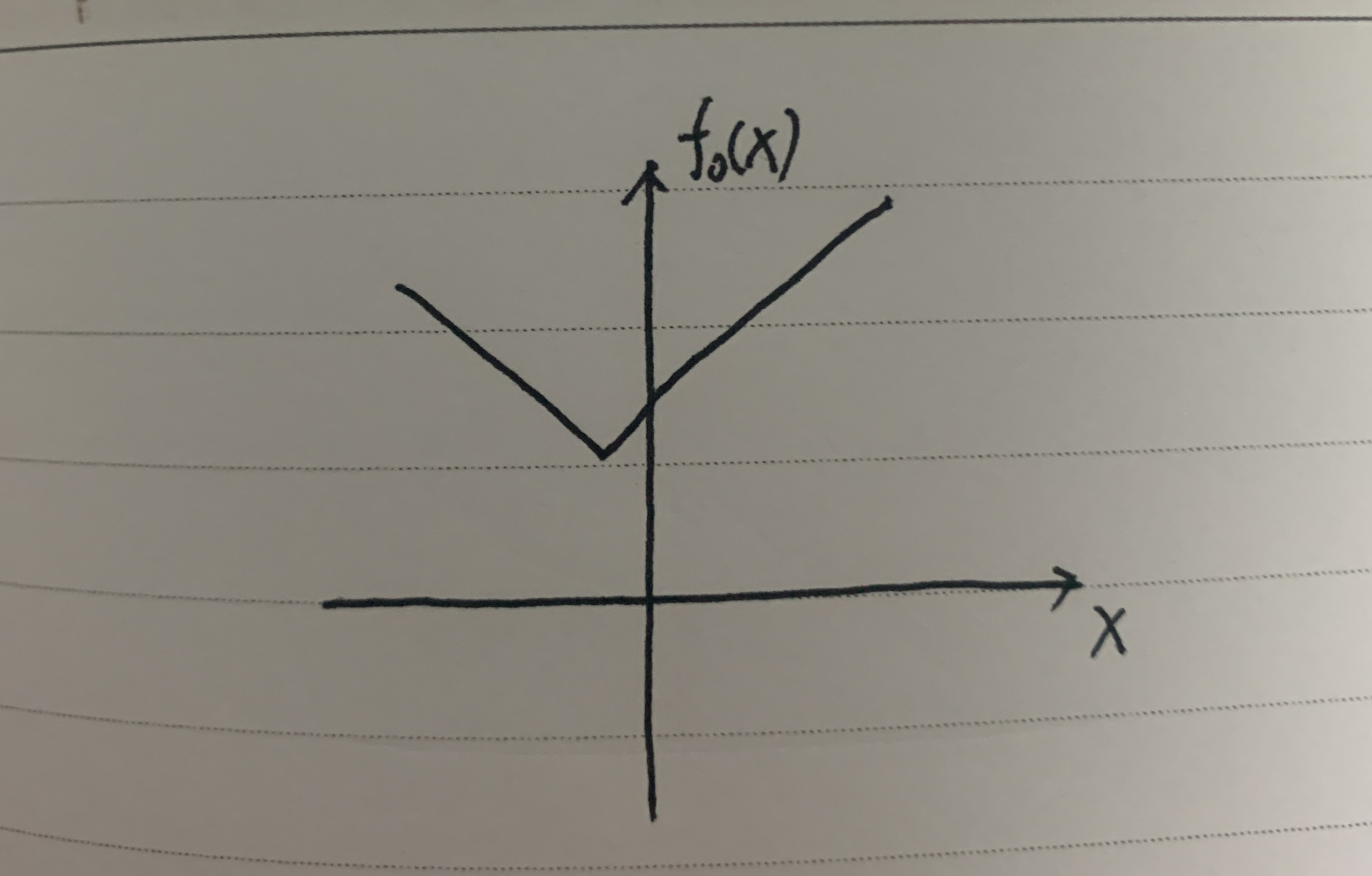
比如说是上图这样的。
光滑的优化问题一般容易一点;非光滑的优化问题一般难一点。但是没有凸规划问题和非凸规划问题差别那么大。
连续/离散
连续和离散是针对可行域的。比如上面线性规划的可行域是连续的。
而离散的优化问题可行域是空间上的一些离散的点:

离散的优化问题一般比较难,但连续的优化问题也不一定容易。
单目标/多目标
上面奖的优化问题其实都是单目标优化问题,即目标函数只有一个。
但实际中很多问题本质上多目标优化问题。
我们主要研究的就是单目标优化问题。
我们主要研究的是凸规划、单目标、目标函数光滑的优化问题。
同时还要知道怎么根据实际需要去构建一些这样容易的问题。