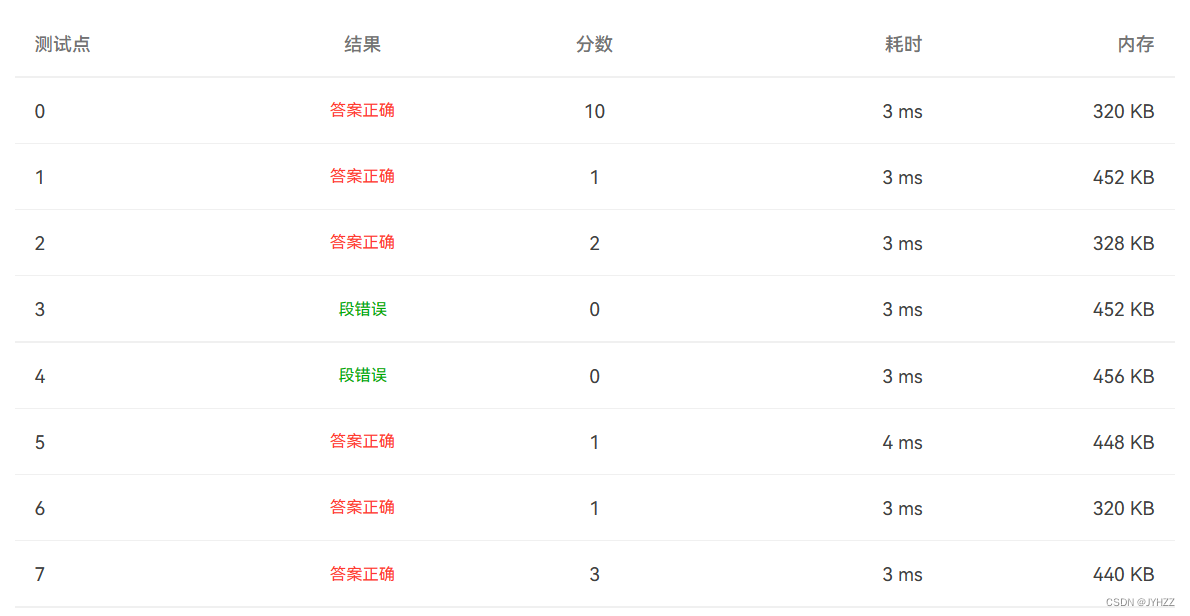
什么是哈希表
在引入哈希表之前,先谈一下为什么要了解哈希表。在学习Set集合时,发现Set集合可以实现无序存储,那么Set是如何实现的无序存储?
打开源码会发现Set集合的底层实际上是由一个map集合实现的。那么什么是哈希表呢?
哈希表(Hash Table)是一种数据结构,也称之为散列表。我们常用的HashMap集合就是哈希表的一种实现,所以我们通常说Set集合的底层是由哈希表实现的。
对于哈希表,在jdk1.8之前的实现方式是:数组+链表+(哈希算法)
jdk1.8时引入了红黑树结构,此时哈希表=数组+链表+红黑树+(哈希算法)
红黑树,是一种实现高效查找的二叉树。其实现机理是根据元素的hashCode的大小决定存放的位置(小的往左,大的往右)。
再回到我们的问题,Set集合如何实现的无序存储?
我们再向Set集合中添加一个数据时,实际上就是向哈希表中添加元素。我们知道每个元素都有一个native的hashCode()方法,JVM会为每个元素分配一个hashCode
hashCode哈希值:通过哈希算法将任意长度的二进制值映射为固定长度的较小二进制值,这个较小二进制值就是元素的哈希值
获取到哈希值之后根据哈希值进行哈希运算获取存储位置再存储到对应的位置上,以此来实现无序存储
哈希表组成
JDK1.8之前
我们已经知道JDK1.8之前哈希表的组成是数组+链表+(哈希算法),我们以HashSet集合为例打开源码查看
// Set集合底层由map实现 HashSet源码
private transient HashMap<E,Object> map;
// 再找到HashMap源码 可以发现哈希表底层的数组就是Node数组
transient Node<K,V>[] table;
Node<k,v>是HashMap类中的一个静态内部类,我们称之为节点。而哈希表中直接存储的就是node节点,Node的主要作用就是用于存储数据。
// Node类
static class Node<K,V> implements Map.Entry<K,V> {
// 元素的hashCode
final int hash;
// 键
final K key;
// 值
V value;
// 下一个元素节点
Node<K,V> next;
. . .
}
哈希表的数组就体现于此,下面我们看典型的哈希算法实现机理:
首先我们创建一个Set集合并添加数据
HashSet<String> sets = new HashSet<String>();
sets.add("元素-1");
sets.add("元素-2");
sets.add("元素-3");
sets.add("元素-4");
sets.add("元素-5");
sets.add("元素-6");
sets.add("元素-7");
哈希算法简单实现
假设哈希表底层数组长度为7(容量满后底层会实现扩容),然后我们开始向散列表中添加数据,过程如图

上图所示,在数据添加的过程中则会产生一种情况:当元素通过哈希算法得到对应的索引位置(可以理解为元素的存储地址)时发现该位置上已经存有元素时,那么当前元素的存储就需要其他方法来解决。这种情况就叫做哈希冲突(后面给到具体讲解),而这里的解决方案就是在对应位置形成链表。
JDK1.8之后
jdk1.8之后引入了红黑树,使散列表查询的性能更佳。红黑树的引用是由开发人员已经再底层封装完毕,并不需要我们去操作。那么红黑树的引用体现在哪里呢?
源码如下:
// 依旧是根据Set集合的add方法依次向上找
// 最终我们会找到HashMap的putVal方法
// putVal方法一大坨判断,下面给出红黑树的部分
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
// binCount就是我们在数组的某个索引处形成的链表长度
// TREEIFY_THRESHOLD 是Java规定的链表最大长度
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
// treeifBin将链表转换为树
treeifyBin(tab, hash);
break;
}
可以发现当我们的链表长度达到8时,底层就会将链表转换为红黑树存储
哈希冲突
前文已经提到了哈希冲突,哈希冲突也叫做哈希碰撞。是指当元素通过哈希函数运算后被映射到哈希表中同一位置的情况。
哈希函数需要尽可能地保证计算简单并且散列地址分布均匀,而数组在内存中是一片连续的区域,所以哈希冲突是都无法避免的,那么哈希冲突的解决办法都有哪些?
前文提到了Set集合,Set集合底层对于哈希冲突的解决方案就是形成链,包括jdk1.8之后的红黑树,实际上也是对哈希冲突的一种解决办法。
解决哈希冲突问题的方法很多,下面给出一部分
- 开放地址法:当出现哈希冲突时,重新去寻找一个新的空闲哈希地址
- 线性探测法:哈希值不断加1,每次加1之后在进行哈希运算直到找到合适的位置,该方法只能单向寻找,性能稍差
- 平方探测法(二次探测):双向寻找位置的方法
- 链地址法:也是经常使用的一种方法,在发生哈希冲突的位置上形成链表,省时省力,但是如果成链元素过多就会大幅降低查询速度
- 再哈希法:同时构建多个哈希函数,如果第一个发生冲突就是用第二个.第三个…(上文图示的哈希算法就是典型的一种)
- 建立公共溢出区:将哈希表分为基本表和溢出表,发生冲突的元素存放在溢出表中
为什么重写equals就要重写hashCode方法
老生常谈的问题了属于是
首先在不重写的情况下我们默认调用的是Object类中的equals方法,如下:
public boolean equals(Object obj) {
return (this == obj);
}
hashCode方法是一个本地方法,每一个对象都有它的hashCode,而hashCode是我们向散列表中添加数据时判断是否重复的关键。
可以看出,默认情况下我们调用equals实际上比较的还是两个对象的地址值是否相同。
在不重写的情况下:a.equals(b)如果==true,那么a和b一定是同一个对象,此时两者的hashcode也一定是相同的。
所以始终围绕一句话:equals为true的两个对象,hashCode一定相同
这也是我们重写这两个方法的核心规则
那么如果只重写了equals方法则可能会出现两个对象完全一致,但是hashCode不同的情况。此时如果我们使用散列集合去存储时就会出现问题,因为散列集合是使用hashCode来决定该元素的存储位置的,如果两个元素equals相同但hashcode不同就会产生两个完全相同的元素存储在散列表中的两个不同位置,如果我们要根据这个对象去获取数据时可能程序就会出现一些预料之外的错误