【人工智能原理自学】一元一次函数感知器：如何描述直觉

news2025/11/1 0:54:27

😊你好，我是小航，一个正在变秃、变强的文艺倾年。
🔔笔记来自B站UP主Ele实验室的《小白也能听懂的人工智能原理》。
🔔本文讲解一元一次函数感知器：如何描述直觉，一起卷起来叭！

一、Python下载安装

跟着官网一步步来就行：https://www.python.org

1.下载：

在这里插入图片描述

在这里插入图片描述

然后选择自己的系统版本，傻瓜式安装！

2.配置环境变量：

在这里插入图片描述

环境测试：
打开windows的命令窗口，输入python：

检查pip是否在环境变量，一般安装Python勾选后就自动设置好了：

给pip配置一个镜像源加速：

pip config set global.index-url https://pypi.tuna.tsinghua.edu.cn/simple

安装Numpy测试速度：

pip install numpy

在这里插入图片描述

3.编译器（这里我使用Pycharm）

官网链接：https://www.jetbrains.com/pycharm/

在这里插入图片描述
Python常用语法、Numpy常用参考：

Python学习手册：https://www.runoob.com/python3/python3-tutorial.html
Numpy学习手册：https://www.runoob.com/numpy/numpy-tutorial.html

二、Rossenblatt感知器

Rosenblatt感知器建立在一个非线性神经元上，即神经元的McCulloch-Pitts模型，这种神经元模型由一个线性组合器和随后的硬限幅器(执行一个符号函数)组成。神经元模型的求和节点计算作用于突触上的输入的线性组合，同时也合并外部作用的偏置。求和节点计算得到的结果，也就是诱导局部域，被作用于硬限幅器。相应地，当硬限幅器输入为正时，神经元输出+1，反之则输出-1。

感知器的符号流图：
在这里插入图片描述
从这个模型我们发现硬限幅器输入或神经元的诱导局部域是：

在这里插入图片描述

核心：通过误差修正参数

在这里插入图片描述

如何调整参数：输入经过函数产生结果，用标准答案减去结果就得到了误差e，要根据e来调整参数。如：w+=e；这样当结果过小时e为正，w增加；过大时e为负，w减小
为什么要乘X：当x为负时就不能是简单的w=w+e了，因为当结果过小时e为正，但w需要向小调整。所以令w=w+e*x，这样就解决了e的符号问题
为什么要乘α，且α要小：如果调整的幅度过大，可能会出现w过小时增大然后过大了，过小时减小又过小了，最后搁那反复横跳。给修正项添加系数a，当a为0.05时每次修正幅度会变慢20倍
数学上是可以证明w最后一定会收敛

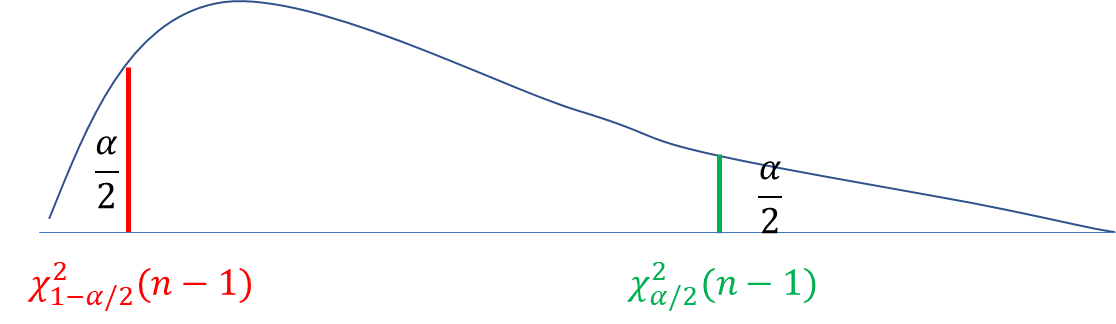
数学证明：
在这里插入图片描述

简言之：朴素但又意义非凡

三、代码实现

豆豆数据集模拟：dataset.py

import numpy as np

def get_beans(counts):
	xs = np.random.rand(counts)
	xs = np.sort(xs)
	ys = [1.2*x+np.random.rand()/10 for x in xs]
	return xs,ys

豆豆预测：beans_predict.py

import dataset
from matplotlib import pyplot as plt
# 拿到随机豆豆100粒
xs, ys = dataset.get_beans(100)
# print(xs)
# print(ys)
# 配置图像
plt.title("Size-Toxicity Function", fontsize=12)
plt.xlabel("Bean Size")
plt.ylabel("Toxicity")
plt.scatter(xs, ys)

# y = 0.5 * w
w = 0.5
for m in range(100):
    for i in range(100):
        x = xs[i]
        y = ys[i]
        y_pre = w * x
        # 误差
        e = y - y_pre
        alpha = 0.05
        w = w + alpha * e * x

y_pre = w * xs
plt.plot(xs, y_pre)
plt.show()