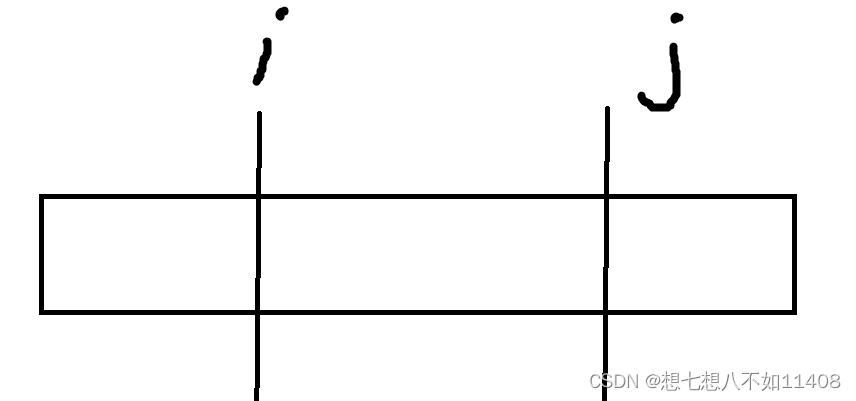
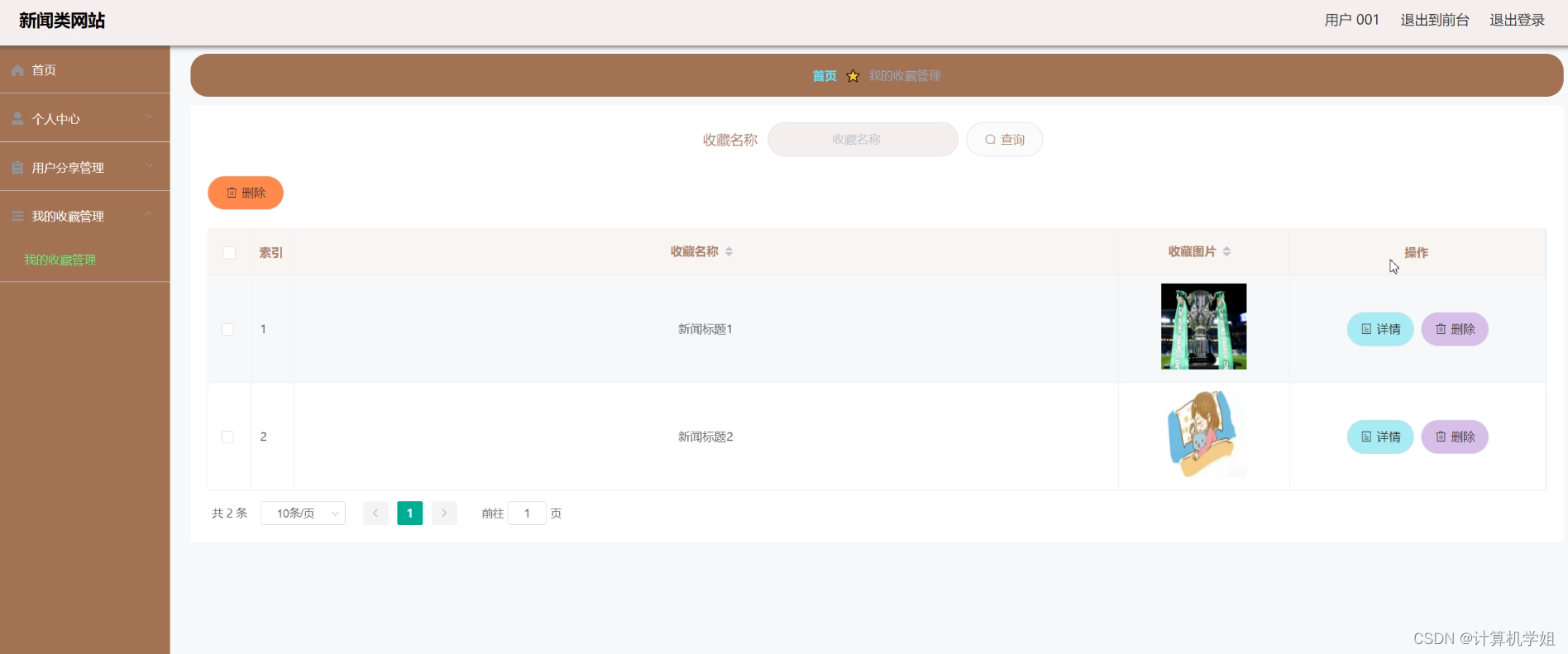
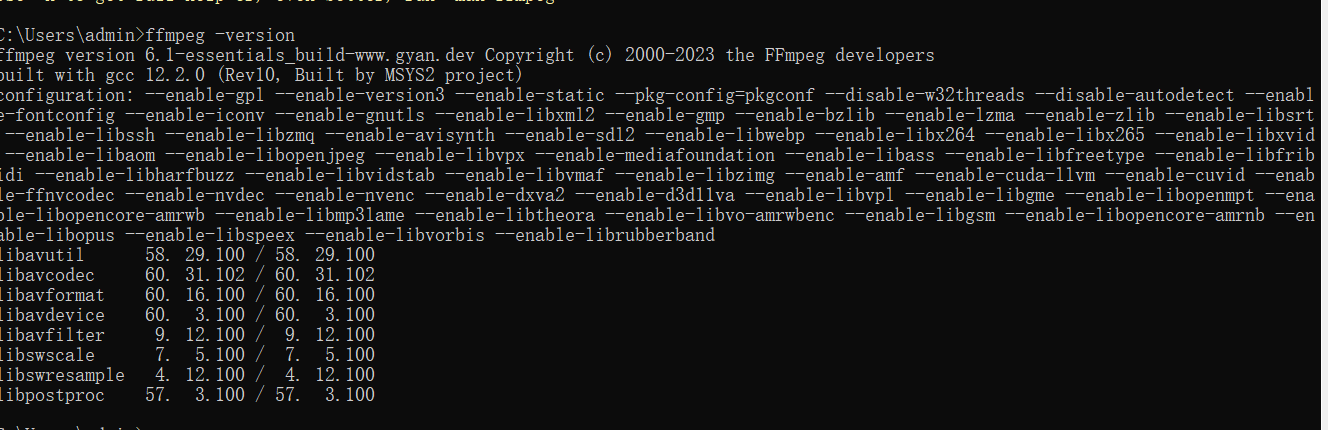
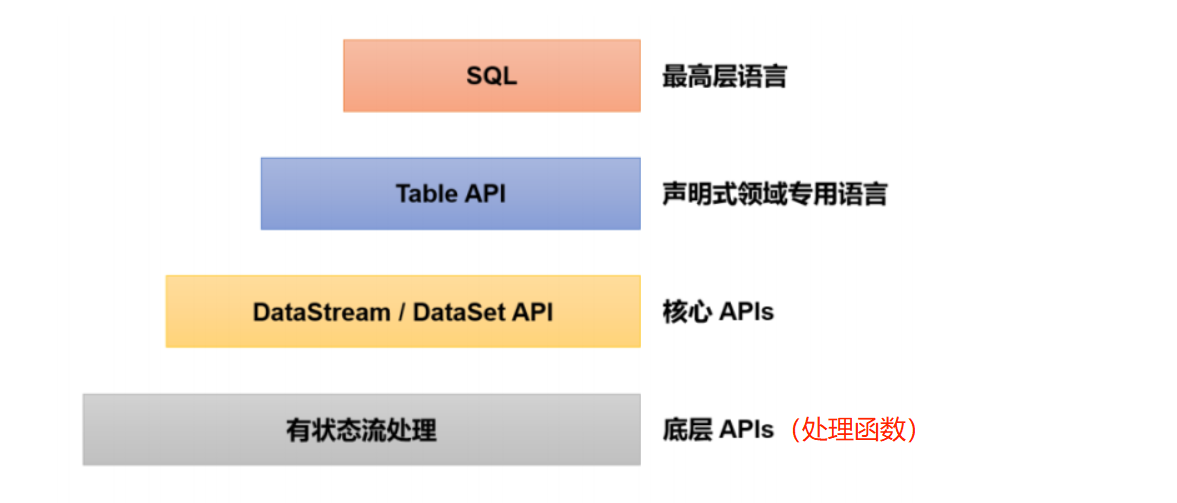
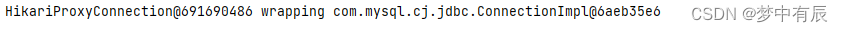原始的SGD

加上动量(惯性,每一次更新根据前面所有结果,使结果更快收敛)

AdaGrad

与SGD的核心区别在于计算更新步长时,增加了分母:梯度平方累积和的平方根。此项能够累积各个参数 的历史梯度平方,频繁更新的梯度,则累积的分母项逐渐偏大,那么更新的步长(stepsize)相对就会变小,而稀疏的梯度,则导致累积的分母项中对应值比较小,那么更新的步长则相对比较大。
AdaGrad能够自动为不同参数适应不同的学习率(平方根的分母项相当于对学习率α进进行了自动调整,然后再乘以本次梯度),大多数的框架实现采用默认学习率α=0.01即可完成比较好的收敛。
优势:在数据分布稀疏的场景,能更好利用稀疏梯度的信息,比标准的SGD算法更有效地收敛。
缺点:主要缺陷来自分母项的对梯度平方不断累积,随之时间步地增加,分母项越来越大,最终导致学习率收缩到太小无法进行有效更新。
RMSProp
![]()
![]()

优势:能够克服AdaGrad梯度急剧减小的问题,在很多应用中都展示出优秀的学习率自适应能力。尤其在不稳定(Non-Stationary)的目标函数下,比基本的SGD、Momentum、AdaGrad表现更良好。
Adam优化器
梯度的指数移动平均数,m0 初始化为0。
算梯度平方的指数移动平均数,v0初始化为0。
![]()
![]()
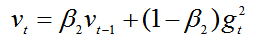
![]()
后期beta1 t就很小,忽略不计了。mt就是改良后的梯度。 m0初始化为0,会导致mt偏向于0,尤其在训练初期阶段。前期学习率为0.0001,更新太慢了。所以,此处需要对梯度均值mt进行偏差纠正,降低偏差对训练初期的影响。
最开始是有梯度的,而不是0,所以是偏差。
![]()
![]()
由表达式可以看出,对更新的步长计算,能够从梯度均值及梯度平方两个角度进行自适应地调节,而不是直接由当前梯度决定。
β1 系数为指数衰减率,控制权重分配(动量与当前梯度),通常取接近于1的值。
默认为0.9
β2 系数为指数衰减率,控制之前的梯度平方的影响情况。默认为0.999
缝合了一下,把rms的gt 换成了mt,并对v和m进行修正。
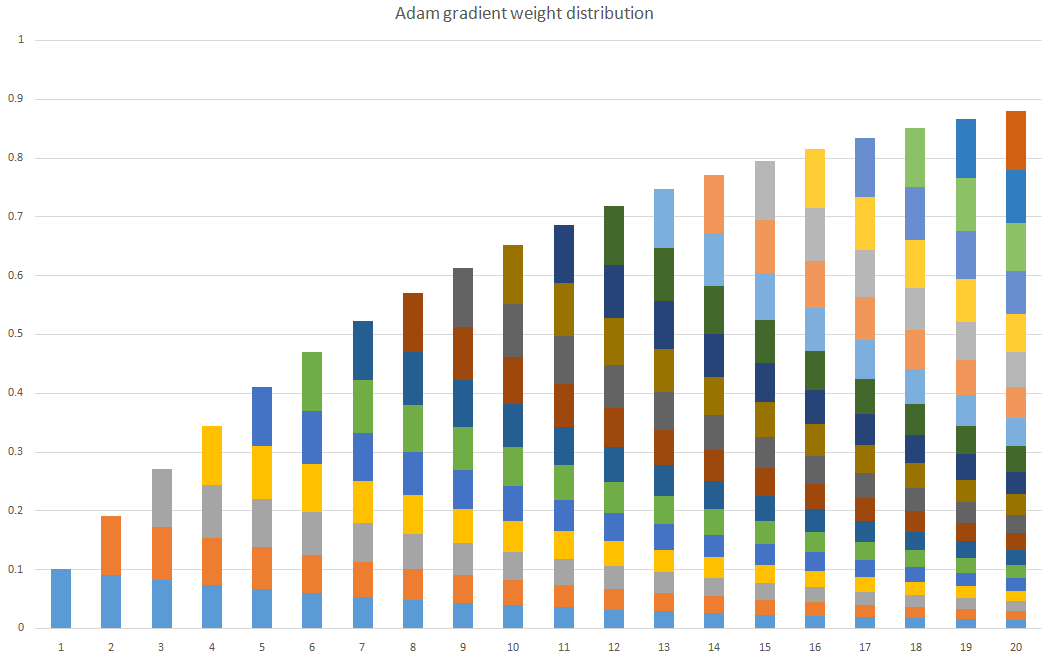
基本上就是0.9的n次方
- 实现简单,计算高效,对内存需求少
- 参数的更新不受梯度的伸缩变换影响
- 超参数具有很好的解释性,且通常无需调整或仅需很少的微调
- 更新的步长能够被限制在大致的范围内(初始学习率)
- 能自然地实现步长退火过程(自动调整学习率)
- 很适合应用于大规模的数据及参数的场景
- 适用于不稳定目标函数
- 适用于梯度稀疏或梯度存在很大噪声的问题
虽然Adam算法目前成为主流的优化算法,不过在很多领域里(如计算机视觉的对象识别、NLP中的机器翻译)的最佳成果仍然是使用带动量(Momentum)的SGD来获取到的。Wilson 等人的论文结果显示,在对象识别、字符级别建模、语法成分分析等方面,自适应学习率方法(包括AdaGrad、AdaDelta、RMSProp、Adam等)通常比Momentum算法效果更差。