Python解题 - CSDN周赛第18期

卧床一周，一觉醒来，恍如隔世，做什么事都提不起兴趣，也不知道这算不算后遗症。

本期的题目还是比较简单的，也有几道做过的题。最后一道照搬过来的背包题也是比较经典的01背包了，整体感觉没有什么值得说的，于是也就一直没更新。

第一题：单链表排序

单链表的节点定义如下（C++）： class Node { public: int element; Node * next; } 实现如下函数：Node * sort(Node * head)，排序以 head 为头结点的单链表，返回排序后列表的 head 节点；只能修改 next 指针，要求时间复杂度和空间复杂度尽可能优化。

分析

说实话，这题我忘得一干二净，完全想不起来考的是什么了。题面上给的是C++的例子，差不多是构建链表的意思，而题目里却没有要求要以链表的数据结构输出，而给的模板也没有构建链表，于是直接将输入的数组进行排序再输出就pass了，这就很搞笑了，完全不懂这样考有什么意义。

参考代码

n = int(input().strip())
arr = [int(item) for item in input().strip().split()]
print(*sorted(arr))

第二题：合并二叉树

已知两颗二叉树，将它们合并成一颗二叉树。合并规则是：都存在的结点，就将结点值加起来，否则空的位置就由另一个树的结点来代替。

例如：两颗二叉树是: Tree 1 1 / 3 2 / 5 Tree 2 2 / 1 3 4 7 合并后的树为 3 / 4 5 / 5 4 7

分析

和第一题一样，这里虽然说是在考二叉树，但却完全没有构建二叉树的数据结构，玩儿一样。而且题目解释得也有问题，比如例子里Tree1和Tree2的格式，Tree2里的空结点并没有用null来表示。不过问题不大，反正也不存在二叉树，在python看来，这只是两个列表的归并排序。

参考代码

n, m = map(int, input().strip().split())
arr1 = input().strip().split()
arr2 = input().strip().split()
result = []
i = j = 0
while i<n and j<m:
    if arr1[i]=="null":
        if arr2[j]=="null":
            result.append("null")
        else:
            result.append(int(arr2[j]))
    else:
        if arr2[j]=="null":
            result.append(int(arr1[i]))
        else:
            result.append(int(arr1[i])+int(arr2[j]))
    i += 1
    j += 1
result.extend(arr1[i:])
result.extend(arr2[j:])
print(*result)

第三题：n边形划分

已知存在 n 多边形，连接多边形所有对角线，能形成多少区域。

分析

这题也没啥好分析的，纯纯的数学题。现成的公式摆在那里， $O(1)$ 的时间复杂度。

$\frac{(n-1)(n-2)(n^2-3n+12)}{24}$

唯一要注意的是python的除法默认会把数据类型转成浮点型，所以要使用整除（//）得到整数型，最后的结果还要对1e9+7取模。

参考代码

n = int(input().strip())
result = (n-1)*(n-2)*(n**2-3*n+12)//24
print(result % 1000000007)

第四题：开心的金明

金明今天很开心，家里购置的新房就要领钥匙了，新房里有一间他自己专用的很宽敞的房间。更让他高兴的是，妈妈昨天对他说：“你的房间需要购买哪些物品，怎么布置，你说了算，只要不超过 N 元钱就行”。今天一早金明就开始做预算，但是他想买的东西太多了，肯定会超过妈妈限定的 N 元。于是，他把每件物品规定了一个重要度，分为5等：用整数1−5表示，第5等最重要。他还从因特网上查到了每件物品的价格（都是整数元）。他希望在不超过 N 元（可以等于 N 元）的前提下，使每件物品的价格与重要度的乘积的总和最大。

设第 $j$ 件物品的价格为 $v[j]$ ，重要度为 $w[j]$ ，共选中了 $k$ 件物品，编号依次为 $j_{1},j_{2},...,j_{k}$ ，则所求的总和为： $v[j_{1}]*w[j_{1}]+v[j_{2}]*w[j_{2}]+...+v[j_{k}]*w[j_{k}]$ 。

请你帮助金明设计一个满足要求的购物单。

第一行，为2个正整数，用一个空格隔开：n,m（其中 N(<30000)表示总钱数，m(<25)为希望购买物品的个数。）

从第2行到第m+1行，第 j 行给出了编号为j−1的物品的基本数据，每行有2个非负整数 v，p（其中 v 表示该物品的价格(v≤10000)，p 表示该物品的重要度(1−5)）

示例：

示例
输入 1000 5
800 2
400 5
300 5
400 3
200 2
输出 3900

分析

又是洛谷原题，估计人家也习惯了。官方题库也是吃紧，如果没有此题，本期都不能被称为竞赛。不过话又说回来，本题也是经典的01背包，虽然没什么难度，但还是有必要熟练掌握的。

所谓01背包，就是指背包里的每种东西只有1件，要么选择放，要么不放，其状态非0即1。本题的“金明的房间”就可以看成是一个“背包”，该“背包”的“容量”就是房间里允许放置的物品总价N，物品之间无重复，而要求的就是在该容量内，放置的物品所能构成的总最大价值是多少。

背包问题是动态规划的一种，有机会我们再单独写篇文章总结一下。简单点说，对新手而言（毕竟问哥也是新手摸索过来的，所以还是比较了解新手，尤其是外行新手的感受），背包模板解法的难度主要有二：1）背包的颗粒度；2）背包空间复杂度的优化。我们拿此题为例，一条条来看。

背包的颗粒度

所谓的“颗粒度”（可能只有问哥这么叫），指的是背包所能容纳的最小物品的体积（本题里指的是物品单价，下同）。理解这一点很关键的原因是，我们是直接利用了数组的下标来表示不同的容量，从而进行回溯和比较。因此，很多题目除非特别提示，默认的背包颗粒度都是1（数组下标的间隔默认都是1）。比如本题里背包的颗粒度也是1，也就是单价为1的物品。但是从示例来看，给出的总价N和每件物品的单价都是100的倍数，所以我们其实也可以尝试把背包的颗粒度变成100来试着解题，这样更省空间（原本需要开1000的数组，颗粒度变成100的话只要开10个）。但是由于题目只明确提到了“每件物品的价格都是整数元”，而并不是“整百”，所以我们不能假设所有的测试数据里都是100的倍数，因此这里我们就用默认的背包颗粒度来开数组即可。

为了求解，我们先按照题目给的数据来列出二维表格如下：

横坐标（每列）表示总价N范围内的每种价格（颗粒度为1，但是为了画图方便，这里简化为颗粒度100），纵坐标（每行）表示每种物品的单价和重要度。需要注意的是，我们在进行背包问题推演求解的过程中，每种物品放入的先后顺序是无关紧要的，这是因为每种物品的背包问题是互相独立的，这也是动态规划应用的基础。而表格中要填写的部分，就是表示在放入可能的物品后，所能构成的最大价值。很显然，我们可以开出一个a[m+1][N+1]的二维数组来表示该表格，而本例中我们要求最大价值N的时候m种物品所能组成的最大价值，就是要求出右下角方格数组元素a[m][N]的值。

之所以需要m+1的行与N+1的列空间，正如你所见，我们需要一个0行0列，来表示什么都不放的时候背包的最大价值，虽然听起来像废话。你也可以把它理解为初始值，而在问哥看来，这一行一列的作用就是为了方便后面的推演计算。所以总而言之，我们需要m+1行、N+1列的数组空间。

下面，我们就可以依次放入物品了（最终结果与放入物品顺序无关），而每放入一件物品，我们都要循环检查这一列，来计算在不同容量的情况下的最优解，而当该列计算完毕，我们放入下一件物品的时候就要以此列数据作为回溯的参考，来进行总价值的比较，从而决定要不要放入下一件物品。

举例来说，当我们放入物品1的时候，由于物品1的单价是800，所以如果背包的容量小于800，我们什么都放不下（这时还无需考虑其他物品），所以只有当容量大于等于800的时候，可以组成的最高总价为1600（800*2），表格更新为下图（我们省略了801、802这样的颗粒度的数据）

（实际上，这一行的数据也是和第0行的数据比较而得来的，每一列和上一行的数据相比，更优的数据放入该行该列。）

接下来，我们放入第2件物品。由于第2件物品的单价更低，总价值更高（400*5=2000），所以和上一行相比，同样容量的情况下，我们优先选择放入第2件物品，而同时我们的总价又无法同时买入两者，所以在800到1000的容量时，我们还是优先放入第2件物品，于是得到更新的表格如下：

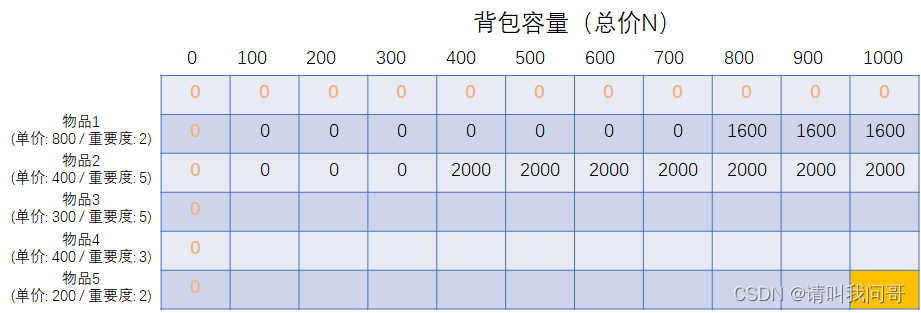
而放入第3件物品的时候，我们就需要考虑得多一点了，因为我们的背包容量是可以同时放入物品2和物品3的，但是在只能二选一的情况时，比如背包容量大于等于400，小于700，优先放入物品2可以获得的总价值更高（和上一行的2000做比较），所以我们在背包容量为400到700之间时，优先放入物品2，而在可以同时放入二者时，背包容量大于等于700，我们可以得到的总价值为二者之和（300*5+400*5=3500）：

现在我们来看第4件物品，这件物品比较特殊，它的单价与第二件物品相同（都是400），但是重要度却更低（只有3），所以，我们在放入的时候，要参考上一行我们已经得到的结果来决定：当背包容量大于等于400时，显然我们放入物品2可获得的总价值更高；而当容量大于等于700时，我们放入物品2和物品3价值更高；显然如果背包容量大于等于1100，我们可以三者都放，但本例背包最大容量只有1000，所以我们这一行的数据和上一行相同，换句话说，除非背包容量大于1100，第4件物品我们不应该选择。更新表格如下：

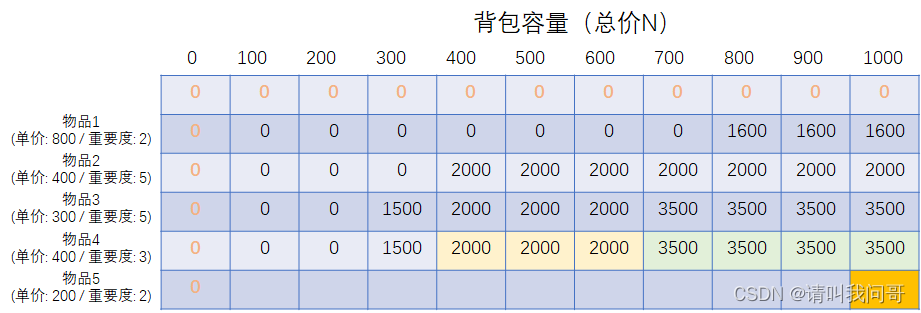
最后，我们放入第5件物品，由于该物品的单价最低，所以我们有了更多可以决定的空间：当背包容量为600时，我们之前只能放入物品2/3/4，但这时我们还可以放入物品5，所以这时背包的总价值可以达到2400，而不是之前的2000。（当背包容量为500时，我们也可以同时放入物品3和物品5，但两者的总价值为1900，要小于单独放物品2的总价值2000，所以此处并没有更新。）当背包容量大于等于900时，我们之前只能放入物品2和物品3，此时我们还可以放入物品5，所以总价值可以达到3900，也就是我们最终的答案。

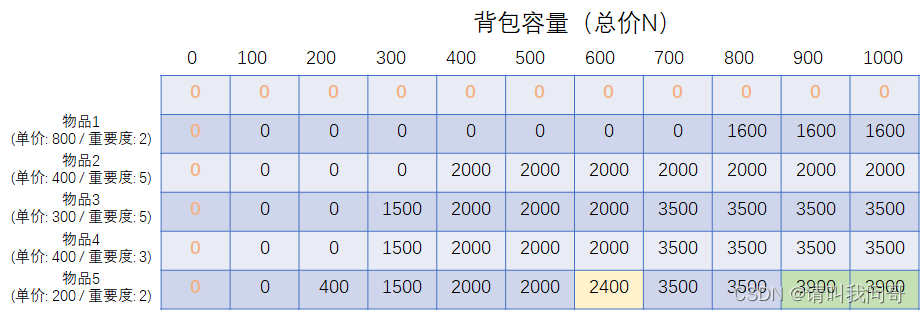
由上面推演的过程，我们可以总结如下规律：

每一行的计算都只需要参考上一行的数据，而与更早的数据无关，因此，物品放入的顺序并不重要。
每一格 $dp[i][j]$ 的计算都是在比较两种情况：①不放入当前物品（上一行的数据 $dp[i-1][j]$ ）；②放入当前物品后，剩下的空间是否还能放其他物品（ $v*p+dp[i-1][j-v]$ ，v*p表示放入当前物品的价值，dp[i-1][j-v]表示放入当前物品后，在上一行里查询剩下的空间所能得到的最大价值）；然后再比较这两种情况所能得到的最大值，放入表格。

上面的第二点又可以写成动态规划的状态转移方程：

$dp[i][j]=max(dp[i-1][j], v*p+dp[i-1][j-v])$

可以看到，这里的 v 既表示了物品的单价，又参与了下标的计算（j - v），这里就显示出颗粒度的重要性，直接使用容量（单价）作为数组下标进行回溯查询，相信这里是部分编程新手的难点之一。

于是，我们把上述推演过程放入循环，用代码表示出来，就可以得到如下解题代码。

参考代码1

n, m = map(int, input().split())
dp = [[0]*(n+1) for _ in range(m+1)] # 创建上图描述的二维表格
for i in range(1, m+1):
    v, p = map(int, input().split()) # 循环m次，得到每件物品的单价和重要度
    for j in range(1, n+1): # 循环计算每一列
        if j < v: continue # 如果单价大于当前背包容量，无法回溯，跳过
        dp[i][j] = max(dp[i-1][j], v*p+dp[i-1][j-v]) # 状态转移方程
print(dp[m][n])

背包空间复杂度的优化

上面的代码代表了01背包问题的基本解题思路，但是，你看到的模板可能会长得不太一样，也许还有的教程会说不同背包循环的方向不同等等。这是因为，在循环的过程中，我们发现二维数组的空间太浪费了。比如我们发现，除了上一行（dp[i-1][j]）的数据以外，之前的数据就完全都不需要了，因此我们可以省去dp[i-2]之外的行数据，只留下dp[i]和dp[i-1]两行数据；而在此基础上更进一步，我们是否真的需要两行数据呢？然后我们发现，如果我们倒序计算的话，只需要一行数据即可，从而将空间复杂度由二维空间压缩到一维。

另外，就此题而言，因为只需要右下角的数据，因此倒序计算的话，最后一件物品的第一个计算结果就是我们要的答案，所以最后一行的数据甚至都不需要完全计算。改进的代码如下：

参考代码2

n, m = map(int, input().split())
dp = [0]*(n+1) # 一维数组空间足矣
for i in range(m-1): # 留下最后一个物品
    v, p = map(int, input().split())
    for j in range(n, v-1, -1): # 倒序计算，计算到背包容量等于物品单价为止
        dp[j] = max(dp[j], v*p+dp[j-v])
v, p = map(int, input().split())
print(max(dp[n], v*p+dp[n-v])) # 最后一个物品只需计算一次即得到答案