文章目录
- 第1关:数塔问题
- 任务描述
- 相关知识
- 编程要求
- 解题思路
- 测试说明
- 参考答案
- 第2关:最长公共子序列
- 任务描述
- 相关知识
- 编程要求
- 解题思路:
- 测试说明
- 参考答案
- 第3关:求序列-2 11 -4 13 -5 -2的最大子段和
- 任务描述
- 相关知识
- 编程要求
- 解题思路:
- 测试说明
- 参考答案
- 第4关:求最长的单调递增子序列长度
- 任务描述
- 相关知识
- 编程要求
- 解题思路:
- 测试说明
- 参考答案
- 第5关:矩阵连乘问题
- 任务描述
- 相关知识
- 编程要求
- 测试说明
- 参考答案
第1关:数塔问题
任务描述
本关任务:编写用动态规划解决数塔问题。
相关知识
为了完成本关任务,你需要掌握:动态规划。
编程要求
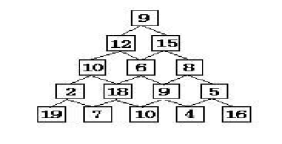
求上图从顶层到顶层的一个路径,使路径上的数字和最大。要求输出最大的数字和max和数值和最大的路径。
解题思路
原始信息有层数和数塔中的数据,层数用一个整型变量n存储,数塔中的数据用二维数组data,存储成如下的下三角阵:
9
12 15
10 6 8
2 18 9 5
19 7 10 4 16
必需用二维数组d存储各阶段的决策结果。二维数组d的存储内容如下:、
d[n][j]=data[n][j], j=1,2,……,n;
d[i][j]=max(d[i+1][j],d[i+1][j+1])+data[i][j], i=n-1,n-2,……1,j=1,2,……,i
最后d[1][1]存储的就是问题的结果。
测试说明
平台会对你编写的代码进行测试:
测试输入:
5
9
12 15
10 6 8
2 18 9 5
19 7 10 4 16
输出示例:
max=59
数值和最大的路径是:9->12->10->18->10
参考答案
#include <stdio.h>
#define N 5 //问题规模
int main() {
int a[50][50];
a[1][1] = 9;
a[2][1] = 12, a[2][2] = 15;
a[3][1] = 10, a[3][2] = 6, a[3][3] = 8;
a[4][1] = 2, a[4][2] = 18, a[4][3] = 9, a[4][4] = 5;
a[5][1] = 19, a[5][2] = 7, a[5][3] = 10, a[5][4] = 4, a[5][5] = 16;
int i, j, dp[50][50] = { 0 }, path[50][50] = { 0 };
for (j = 1; j <= N; j++) //初始子问题 ,倒数第二层(第i-1层)开始
dp[N][j] = a[N][j];
for (i = N - 1; i >= 1; i--) //进行第 i+1 层的决策,从i 到 1 向上
for (j = 1; j <= i+1; j++) { //每一层有 i+1 个
if (dp[i + 1][j] > dp[i + 1][j + 1]) {
dp[i][j] = a[i][j] + dp[i + 1][j];
path[i][j] = j; //本次决策选择下标j的元素
}
else {
dp[i][j] = a[i][j] + dp[i + 1][j + 1];
path[i][j] = j + 1; //本次决策选择下标j+1的元素
}
}
printf("max=%d\n", dp[1][1]);
printf("数值和最大的路径是:");
j = path[1][1]; //计算dp[1][1]的选择
for (i = 1; i < N; i++)
{
printf("%d->", a[i][j]);
j = path[i][j]; //计算dp[i][j]的选择
}
printf("%d\n", a[i][j]);
}
/********** End **********/
第2关:最长公共子序列
任务描述
本关任务:编写用动态规划解决最长公共子序列问题。
相关知识
为了完成本关任务,你需要掌握:动态规划。
编程要求
求字符串序列“ABCDBAB”和“BDCABA”的最长公共子序列
解题思路:
递推关系分析: 设 A=“a0,a1,…,am−1”,B=“b0,b1,…,bn−1”,Z=“z0,z1,…,zk−1” 为它们的最长公共子序列。 有以下结论: 1)如果am−1=bn−1,则zk−1=am−1=bn−1,且“z0,z1,…,zk−2”是“a0,a1,…,am−2”和“b0,b1,…,bn−2”的一个最长公共子序列; 2)如果am−1=bn−1,则若zk−1=am−1,蕴涵“z0,z1,…,zk−1”是“a0,a1,…,am−2”和“b0,b1,…,bn−1”的一个最长公共子序列; 3)如果am−1=bn−1,则若zk−1=bn−1,蕴涵“z0,z1,…,zk−1”是“a0,a1,…,am−1”和“b0,b1,…,bn−2”的一个最长公共子序列。 定义c[i][j]为序列“a0,a1,…,ai−1”和“b0,b1,…,bj−1”的最长公共子序列的长度,计算c[i][j]可递归地表述如下: 1)c[i][j]=0 如果i=0或j=0; 2)c[i][j]=c[i−1][j−1]+1 如果i,j>0,且a[i−1]=b[j−1]; 3)c[i][j]=max(c[i][j−1],c[i−1][j]) 如果i,j>0,且a[i−1]=b[j−1]。 由二维数组c的递归定义,c[i][j]的结果依赖于c[i−1][j−1],c[i−1][j]和c[i][j−1]。可以从c[m][n]开始,跟踪c[i][j]结果的产生过程,从而逆向构造出最长公共子序列。
测试说明
平台会对你编写的代码进行测试:
测试输入:
a=“ABCDBAB”
b=“BDCABA”
输出示例:
BCBA
参考答案
/*动态规划之最大子序列*/
#include <stdio.h>
int main()
{
char A[7]={'A','B','C','B','D','A','B'};
char B[6]={'B','D','C','A','B','A'};
int dp[8][7]; //dp数组记录最长公共子序列的长度
for(int i=0;i<7;i++) //边界赋值为0
{
dp[i][0]=0;
}
for(int i=0;i<8;i++)
{
dp[0][i]=0;
}
// printf("test1=%d\n",dp[6][7]);
for(int i=1;i<=7;i++)
{
for(int j=1;j<=6;j++)
{
if(A[i-1]==B[j-1]) //如果相等就dp[i][j]=dp[i-1][j-1]+1;
{
dp[i][j]=dp[i-1][j-1]+1;
}
else{
if(dp[i-1][j]>dp[i][j-1])
{
dp[i][j]=dp[i-1][j]; //取两者之间较大者;局部的最优值
}
else{
dp[i][j]=dp[i][j-1];
}
}
}
}
char str[100]; //记录公共的字符
int i=7,j=6;
int count=0;
while(i>0&&j>0)
{
if(dp[i][j]==dp[i-1][j]) //往上遍历
{
i--;
}
else if(dp[i][j]==dp[i][j-1]) //往左遍历
{
j--;
}
else{
str[count++]=A[i-1];
i--;
j--;
}
}
for(int i=count-1;i>=0;i--)
{
printf("%c",str[i]);
}
}
第3关:求序列-2 11 -4 13 -5 -2的最大子段和
任务描述
本关任务:编写用动态规划解决最大子段和问题。
相关知识
为了完成本关任务,你需要掌握:动态规划。
编程要求
给定由n个整数(可能为负数)组成的序列:a1,a2,……,an, 求该序列的最大子段和。当所有整数均为负数,定义其最大子段和为0。
解题思路:
定义b[j]=max(a[i]+a[i+1]+…+a[j]),其中1<=i<=j,并且1<=j<=n。那么所求的最大子段和可以表示为max b[j],1<=j<=n。 由b[j]的定义可知,当b[j−1]>0时b[j]=b[j−1]+a[j],否则b[j]=a[j]。故b[j]的动态规划递归表达式为: b[j]=max(b[j−1]+a[j],a[j]),1<=j<=n。
测试说明
平台会对你编写的代码进行测试:
测试输入:
6
-2 11 -4 13 -5 -2
输出示例:
20
参考答案
#include <stdio.h>
/********** Begin **********/
int main(){
int n;
scanf("%d",&n);
int a[n][2];
int max=0;
for(int i=0;i<n;i++){
scanf("%d",&a[i][0]);
if(i==0){
a[i][1]=a[i][0];
}
else{
a[i][1]=a[i-1][1]+a[i][0]>a[i][0]?a[i-1][1]+a[i][0]:a[i][0];
}
max=max>a[i][1]?max:a[i][1];
}
printf("%d",max);
return 0;
}
/********** End **********/
第4关:求最长的单调递增子序列长度
任务描述
本关任务:编写用动态规划解决求最长的单调递增子序列长度问题。
相关知识
为了完成本关任务,你需要掌握:动态规划。
编程要求
给定一个长度为n的数组,找出一个最长的单调递增子序列(不一定连续,但是顺序不能乱)。例如:给定一个长度为7的数组A5,6,7,1,2,8,9,则其最长的单调递增子序列为5,6,7,8,9,长度为5。求318714101223411624的最长的单调递增子序列长度。
解题思路:
设长度为n的数组为(a[0],a[1],a[2],…,a[n−1]),则假定以a[j]结尾的数组序列的最长递增子序列长度为L(j),则L(j)=max(L(i))+1,i<j且a[i]<a[j]。也就是说,我们需要遍历在j之前的所有位置i(从0到j−1),找出满足条件a[i]<a[j]的L(i),求出max(L(i))+1即为L(j)的值。最后,我们遍历所有的L(j)(从0到n−1),找出最大值即为最大递增子序列。
测试说明
平台会对你编写的代码进行测试:
测试输入:
10
3 18 7 14 10 12 23 41 16 24
输出示例:
6
参考答案
#include <stdio.h>
/********** Begin **********/
int main(){
int n;
scanf("%d",&n);
int m[n][3];
m[0][1]=1;
m[0][2]=0;
for(int i=0;i<n;i++){
scanf("%d",&m[i][0]);
if(i!=0){
m[i][1]=0;
int k=i-1;
while(k>=0){
if(m[i][0]>m[k][0]){
if(k==i-1){
m[i][1]=m[k][1]+1;
m[i][2]=k;
}
else{
int max=m[k][1]+1;
if(max>m[i][1]){
m[i][1]=max;
m[i][2]=k;
}
}
}
k--;
}
if(k<0&&m[i][1]==0){
m[i][1]=1;
m[i][2]=i;
}
}
}
int max=m[0][1],j=0;
for(int i=0;i<n;i++){
if(m[i][1]>=max){
max=m[i][1];
j=i;
}
}
printf("%d\n",max);
}
/********** End **********/
第5关:矩阵连乘问题
任务描述
本关任务:编写用动态规划解决矩阵连乘问题。
相关知识
为了完成本关任务,你需要掌握:动态规划。
编程要求
将矩阵连乘积AiAi+1…Aj简记为A[i:j],其中i<=j。设在矩阵Ak和Ak+1之间将矩阵链断开,则其相应加括号为(AiAi+1…Ak) (Ak+1Ak+2…Aj)。A[i:j]的计算量等于三部分计算量之和: (1)A[i:k]的计算量, (2)A[k+1:j]的计算量, (3)A[i:k]与A[k+1:j]相乘的计算量。 设计算A[i:j]所需最少乘积数目为,则原问题的最优值为。 当i=j时,a[i:j]=Ai,因此,m[i][j]=0,i=1,⋅⋅⋅,n 当i<j时,m[i][j]=i<k<jmin{m[i][k]+m[k+1][j]+pi−1pkpj} 其中,矩阵Ai的矩阵数为pi−1×pi 矩阵A1的维度:p0p1=3035 矩阵A2的维度:p1p2=3515 矩阵A3的维度:p2p3=155 矩阵A4的维度:p3p4=510 矩阵A5的维度:p4p5=1020 矩阵A6的维度:p5p6=2025 求这6个矩阵连乘的最小相乘次数。
测试说明
平台会对你编写的代码进行测试:
测试输入:
6
30 35
35 15
15 5
5 10
10 20
20 25
输出示例:
m[1][6]=15125
参考答案
#include <stdio.h>
#include <stdlib.h>
/********** Begin **********/
int main(){
int n;
scanf("%d",&n);
int a[n][2];
int b[n][n]={0};
for(int i=0;i<n;i++){
scanf("%d %d",&a[i][0],&a[i][1]);
}
for(int i=1;i<n;i++){
for(int j=0;j<n-i;j++){
b[j][j+i]=b[j][j]+b[j+1][j+i]+a[j][0]*a[j][1]*a[j+i][1];
int k=j+1;
for(;k<j+i;k++){
int t=b[j][k]+b[k+1][j+i]+a[j][0]*a[k][1]*a[j+i][1];
if(t<b[j][j+i]) {
b[j][j+i]=t;
}
}
}
}
printf("m[%d][%d]=%d",1,n,b[0][n-1]);
return 0;
}
/********** End **********/