JavaSE学习笔记 Day20
个人整理非商业用途,欢迎探讨与指正!!
« 上一篇
文章目录
- JavaSE学习笔记 Day20
- ···
- 十七、数据结构与算法
- 17.1算法
- 17.1.1冒泡排序
- 17.1.2选择排序
- 17.1.3插入排序
- 17.1.4三个排序的区别
- 17.2顺序表
- 17.2.1顺序表代码实现
- 17.2.2顺序表的问题
- 17.2.3顺序表的扩容问题解决
- 17.3链表
- 17.3.1链表的代码实现
- 17.4树
- 17.4.1树的相关名称
- 17.4.2树的分类
- 17.4.3二叉树
···
十七、数据结构与算法
排序算法,线型结构,树型结构,图…
17.1算法
在计算机中实现数学公式或者数学逻辑
17.1.1冒泡排序
相邻的两个数进行比较,大的向后,反复这样的操作
public class Demo01 {
// 编写冒泡排序算法的方法
public static int[] range(int ...args) {
for(int i = 0;i<args.length - 1;i++) {
for(int j = 0;j<args.length - 1 - i;j++) {
// 两个数进行比较,大的数值向后
if(args[j] > args[j + 1]) {
int temp = args[j];
args[j] = args[j+1];
args[j+1] = temp;
}
}
}
return args;
}
public static void main(String[] args) {
int[] range = range(10,20,31,14,200,30);
for (int i : range) {
System.out.println(i);
}
}
}
17.1.2选择排序
算法描述
在未排序的序列中找到一个最大(小),存放到需要排序的序列最开始的位置
然后再从剩余的未排序的元素中继续寻找最大(小),然后排放到已排序的末尾
以此类推,直到所有元素都排序完毕
// 1.从未排序的数组中找到最小值
public class Test01 {
public static void main(String[] args) {
// 定义未排序的数组
int[] arr = {1,4,123,5,3,1235,5,2,4};
// 遍历数组找到最小的元素
// 假定最小的元素为 第0个位置
int minValue = arr[0];
// 通过循环判断出真实的最小值
for(int i = 0;i<arr.length;i++) {
// 所有位置都和最小值去比较
if(arr[i] < minValue) {
// 更新最小值
minValue = arr[i];
}
}
System.out.println("最小值为:"+minValue);
}
}
// 2.将最小值和没有排序的数组的一个元素进行交换
public class Test02 {
public static void main(String[] args) {
// 定义未排序的数组
int[] arr = {4,123,5,3,1235,5,2,4,1};
// 遍历数组找到最小的元素
// 定义一个下标,获取到最小的下标
int minPosition = 0;
// 通过循环判断出真实的最小值
for(int i = 0;i<arr.length;i++) {
// 所有位置都和最小值去比较
if(arr[i] < arr[minPosition]) {
// 获取最小值的下标
minPosition = i;
}
}
System.out.println("最小值为:"+arr[minPosition]);
System.out.println("最小值的下标:"+minPosition);
// 将最小值更换到0的位置
int temp = arr[0];
arr[0] = arr[minPosition];
arr[minPosition] = temp;
System.out.println(Arrays.toString(arr));
}
}
// 3.将未排序的数组,重复的进行1和2步
public class Test03 {
public static void main(String[] args) {
int[] arr = {4,123,5,3,1235,5,2,4,1};
// 定义循环变量
int start = 0;
int minPosition = start;
for(int i = start;i<arr.length;i++) {
if(arr[i] < arr[minPosition]) {
minPosition = i;
}
}
System.out.println("最小值为:"+arr[minPosition]);
System.out.println("最小值的下标:"+minPosition);
int temp = arr[start];
arr[start] = arr[minPosition];
arr[minPosition] = temp;
System.out.println(Arrays.toString(arr));
// 重复的执行start = 1 start = 2 ... 时的变化
}
}
// 4.使用循环去完成整个算法的优化
// 将未排序的数组,重复的进行1和2步
public class Test04 {
public static int[] range(int ...arr) {
//start不是随意的,start表示的是下标
for(int start = 0;start < arr.length;start ++) {
int minPosition = start;
for(int i = start;i<arr.length;i++) {
if(arr[i] < arr[minPosition]) {
minPosition = i;
}
}
int temp = arr[start];
arr[start] = arr[minPosition];
arr[minPosition] = temp;
}
return arr;
}
public static void main(String[] args) {
int[] arr = {4,123,5,3,1235,5,2,4,1};
arr = range(arr);
System.out.println(Arrays.toString(arr));
}
}
17.1.3插入排序
算法描述:
1.从第一个元素开始,该元素被认定为已经排序
2.取出下一个数,在已经排序的元素序列从后向前扫描
3.若该元素(已排序的)大于新元素,该元素向下移位
4.重复第3步,直到找到已排序的元素小于或者等于新的元素位置
5.将新的元素插入到该位置
6.重复2-5
public class Test02 {
// 1.从没有排序的数组中取出一个元素,和已排序的数组中的内容进行比较,小的向前
public static void main(String[] args) {
int[] arr = {8,6,4,7,44,3,21};
// 认为arr[0]是有序的
// 取出一个值
int insert = arr[1];
// 判断大小
if(arr[0] > insert) {
// 若大则向后
arr[1] = arr[0];
}
// 安排取出来的值
arr[0] = insert;
System.out.println(Arrays.toString(arr));
// 0 1有序
// 取一个值
insert = arr[2];
if(arr[1] > insert) {
// 大的值向后
arr[2] = arr[1];
}
if(arr[0] > insert) {
// 大的值向后
arr[1] = arr[0];
}
// 安排取出去的值
arr[0] = insert;
System.out.println(Arrays.toString(arr));
insert = arr[3];
if(arr[2] > insert) {
// 大的向后
arr[3] = arr[2];
}
if(arr[1] > insert) {
// 大的向后
arr[2] = arr[1];
}else {
// 若不大,则插入到指定的位置
arr[2] = insert;
}
System.out.println(Arrays.toString(arr));
insert = arr[4];
if(arr[3] > insert) {
arr[4] = arr[3];
}
if(arr[2] > insert) {
arr[3] = arr[2];
}
System.out.println(Arrays.toString(arr));
insert = arr[5];
if(arr[4] > insert) {
arr[5] = arr[4];
}
if(arr[3] > insert) {
arr[4] = arr[3];
}
if(arr[2] > insert) {
arr[3] = arr[2];
}
if(arr[1] > insert) {
arr[2] = arr[1];
}
if(arr[0] > insert) {
arr[1] = arr[0];
}
arr[0] = insert;
System.out.println(Arrays.toString(arr));
insert = arr[6];
if(arr[5] > insert) {
arr[6] = arr[5];
}
if(arr[4] > insert) {
// 大的向后
arr[5] = arr[4];
}else {
// 不大说明到地方了
arr[5] = insert;
}
System.out.println(Arrays.toString(arr));
}
}
public class Test04 {
public static int[] range(int ...arr) {
for(int index = 1;index<arr.length;index++) {
int insert = arr[index];
while(index > 0) {
if(arr[index-1] > insert) {
arr[index] = arr[index - 1];
}else {
arr[index] = insert;
break;
}
index --;
if(index == 0) {
arr[0] = insert;
}
}
}
return arr;
}
public static void main(String[] args) {
int[] arr = {8,6,4,7,44,3,21,-1};
arr = range(arr);
System.out.println(Arrays.toString(arr));
}
}
17.1.4三个排序的区别
冒选插都使用了循环,并且基本上都是遍历所有的元素,时间复杂度都是O(N^2)
有一些细微的差别
冒泡,书写最简单的,但是性能没有另外两个好,比较次数和轮数是最多的
选择,比较次数比较多,但是交换次数少
插入,交换的次数多,但是比较次数会相对少一些
17.2顺序表
内存中以数组的形式,保存的一种数据结构,使用一连串的内存地址线性的存储数据的
17.2.1顺序表代码实现
public class MyArrayList<T> {
// 存储的元素
private T[] items;
// 存储数据的有效数值
private int size;
// 添加构造方法
public MyArrayList(int capacity) {
// capacity容量
}
// 获取当前集合的元素个数
public int size() {
return size;
}
// 添加到数组 添加到数组的尾部
public void add(T t) {
// 设计扩容方法
}
// 返回指定下标的元素
public T get(int i) {
return items[i];
}
// 移除
public T remove(int i) {
// 下标是否合法
// 将后面的内容向前移动
// 将最后一个位置设置为null
return items[i];
}
}
17.2.2顺序表的问题
扩容问题,数组的长度的是固定的,没有空间时就会抛出数组下标越界异常
ArrayIndexOutOfBoundsException
17.2.3顺序表的扩容问题解决
1.自定义扩容算法
2.System的arrayCopy(原数组,原数组拷贝的下标,新数组,新数组拷贝的下标,拷贝的长度)
3.Arrays的copyOf(原数组,新数组的长度)底层调用的是System的arrayCopy
17.3链表
顺序表,内存连续,查询快,删除修改慢
链表是概念上逻辑上的连续,内存中并不连续,物理地址中存放是不连续的,无顺序的
插入和删除修改性能特别高
查询效率低
17.3.1链表的代码实现
链表不是使用数组实现的,而是通过节点实现的
// 单链表
public class Node<T> {
T item;//存储当前节点元素
Node next;//下一元素
public Node(T item,Node next){
this.item = item;
this.next = next;
}
}
// 双链表
public class Node2<T> {
Node2<T> pre;//上一个
T item;//当前的
Node2<T> next;//下一个
public Node2(Node2<T> pre,T item,Node2<T> next) {
this.pre = pre;
this.item = item;
this.next = next;
}
public static void main(String[] args) {
// 就是双链表中的唯一数据
Node2<String> n1 = new Node2<String>(null, "helloworld", null);
Node2<String> n2 = new Node2<String>(n1, "嘿嘿", null);
Node2<String> n3 = new Node2<String>(n2, "嘎嘎", null);
}
}
17.4树
树这种数据结构可以同时提高存储和检索的效率
数的特征:
1.数由n个有限节点组成一个有层次关系的集合
2.每个节点都有0个或多个子节点
3.没有父节点的成为根节点
4.每个非根节点,只有一个父节点
5.除了根节点以外,每个子节点都可以分为多个不相交的子树
17.4.1树的相关名称
节点:树中存储数据的对象
根节点:树中唯一没有父节点的节点
父节点:节点的上一层节点,每个节点最多只有一个父节点
子节点:节点的下一层节点,每个节点可以有多个子节点或者没有
叶子节点:没有子节点的节点
节点的度:节点的子节点数量
树的度:一颗树中,最大节点的度称为树的度
路径:从根节点到当前节点的路径
节点的层:从根节点开始,根节点为1层,下一层为2层,以此类推
高度:数的最大层
森林:有n棵不相交的树的组成的集合称为森林,若一棵树根节点删除,那么会变成一个森林
17.4.2树的分类
二叉树:
每个父节点只有两个子节点
查找数:
平衡树和红黑树
带权树:
最优二叉数
多叉数:
每个父节点超过两个子节点
B_树,B+树
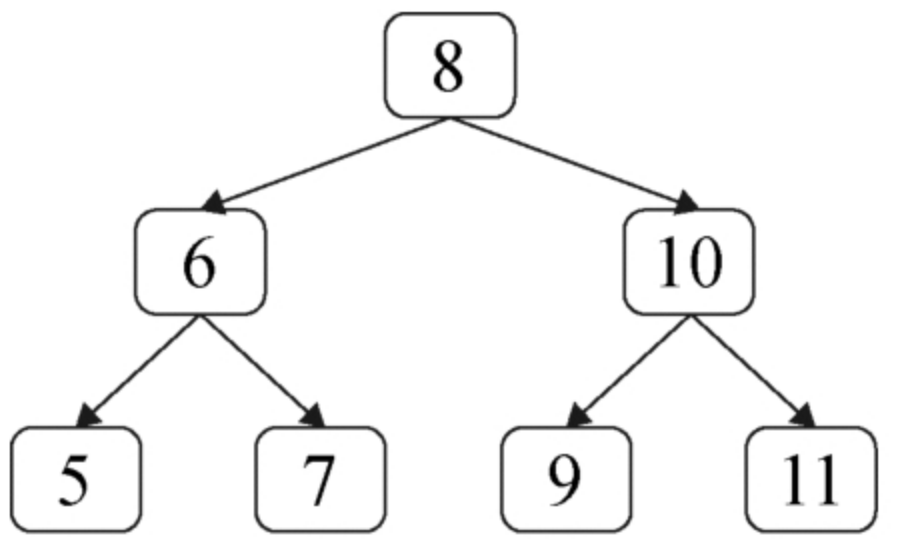
17.4.3二叉树
二叉树的度:2
满二叉树:每个节点都是饱和状态
完全二叉树:最后一层的节点数,从左向右是连续的(满二叉树是完全二叉树的天特殊情况)
树的遍历
将所有的节点都访问一次,只有一次
前序遍历:根左右
中序遍历:左根右
后序遍历:左右根

前序/先序:1 245 367
中序:425 1 637
后序:452 673 1