这个标题涉及到碳捕集、电力转化为气体（可能是指电力转化为氢气等）、矿区综合能源系统以及协同优化调度等概念。让我们逐步解读：

1. 碳捕集（Carbon Capture）： 这指的是通过不同技术手段捕获和隔离工业过程中产生的二氧化碳（CO2），以减缓或防止其释放到大气中，从而减少温室气体排放。

2. 电转气（Electricity to Gas）： 这表示将电能转化为气体能源，其中气体的形式可以是氢气（电解水得到氢气）或其他可储存的气体，这通常用于能源储存和传输。

3. 矿区综合能源系统： 这是指在矿区（可能是指采矿业或矿产资源相关的区域）中，通过整合多种能源形式，包括电力、气体等，形成一个综合的能源系统。

4. 协同优化调度： 这意味着对整个系统中的各种能源元素进行协同优化调度，以实现最佳的能源利用和效率。这可能涉及到优化能源生产、储存、转化和使用的时间和量，以满足矿区的能源需求。

因此，整个标题的意思可能是，针对某个矿区，通过采用碳捕集技术、将电能转化为气体能源，建立一个综合的能源系统，并通过协同优化调度来提高整个系统的能源效率，同时降低温室气体排放。这可能是一个面向可持续发展和低碳经济的研究或工程项目。

摘要：“双碳”战略目标下，为促进风光消纳与能源电力低碳转型、提高矿区能源利用率，提出一种含伴生能源和碳捕集与电转气耦合的矿区综合能源系统低碳经济调度模型。首先，综合考虑瓦斯、乏风、涌水等矿区伴生能源利用，建立矿区综合能源系统基本模型，并以碳捕集和电转气设备为耦合单元，促进节能减排与可再生能源消纳。然后，引入奖惩阶梯式碳交易机制，以矿区综合能源系统运行成本最小为目标，建立矿区综合能源系统协同优化调度模型。最后，以中国云南某大型煤矿为例，通过设置不同场景进行仿真分析，结果表明所提模型能够促进矿区综合能源系统低碳经济运行，提高风光消纳率。

这段摘要涉及到在“双碳”战略目标下，为实现风光能源的消纳、能源电力的低碳转型，以及提高矿区能源利用率，提出了一种综合能源系统的低碳经济调度模型。以下是摘要的主要解读：

1. 双碳战略目标： 这可能指的是中国提出的“双碳”目标，即碳达峰和碳中和。碳达峰意味着碳排放量在未来将会达到峰值并逐渐下降，而碳中和则表示减排措施与碳吸收相抵消，实现零碳排放。

2. 促进风光消纳与能源电力低碳转型： 该研究的目标之一是推动风光能源的消纳，即提高利用风光能源的能力，并推动能源电力向更低碳方向发展。

3. 提高矿区能源利用率： 研究旨在提高矿区对能源的有效利用，可能包括优化能源生产、转化和使用的过程，以提高整体效率。

4. 伴生能源和碳捕集与电转气耦合的矿区综合能源系统低碳经济调度模型： 该模型考虑了矿区产生的伴生能源（如瓦斯、乏风、涌水等），并将碳捕集和电转气设备作为耦合单元，以实现能源系统的协同运作，从而达到低碳经济目标。

5. 奖惩阶梯式碳交易机制： 引入了一种奖惩机制，可能是通过碳交易的方式，根据矿区综合能源系统的碳排放状况进行奖励或处罚，以鼓励低碳行为。

6. 以云南某大型煤矿为例的仿真分析： 最后，通过对云南某大型煤矿不同场景的仿真分析，验证了所提出的模型在促进矿区综合能源系统低碳经济运行和提高风光能源消纳率方面的有效性。

总体来说，这项研究旨在为矿区能源系统的低碳优化提供一个综合的调度模型，并通过仿真验证表明该模型在实际案例中是可行的和有效的。

关键词:矿区综合能源系统;碳捕集;电转气:矿区伴生能源:阶梯式碳交易机制;

1. 矿区综合能源系统 (Integrated Energy System in Mining Areas):

   • 这指的是一个综合考虑多种能源来源（包括传统和可再生能源）的系统，旨在提高能源效率、降低碳排放，并使能源在矿区内得到更有效的利用。

2. 碳捕集 (Carbon Capture):

   • 这是一种技术，旨在捕获产生的二氧化碳，通常来自工业过程或能源生产，以防止其释放到大气中，从而减少温室气体排放。

3. 电转气 (Power-to-Gas):

   • 这是一种技术，其中电能被用来产生氢气或其他可燃气体，这些气体可以在需要时作为能源储存或用于其他工业过程。

4. 矿区伴生能源 (Associated Energy in Mining Areas):

   • 指在矿区生产过程中产生的额外能源，可能包括瓦斯、乏风、涌水等，这些能源可以被有效地利用，从而提高能源的综合利用率。

5. 阶梯式碳交易机制 (Tiered Carbon Trading Mechanism):

   • 这是一种碳交易的机制，可能采用奖励和惩罚的形式，根据参与者在减排方面的表现，制定不同层次的碳交易政策。这可以激励低碳行为，并提供经济动力来减少碳排放。

综合来看，这些关键词揭示了一种在矿区中推动可持续发展的综合能源管理系统，涵盖了能源来源的多样性、碳排放控制、能源转化技术以及通过市场机制激励低碳行为的手段。这表明对矿区综合能源系统进行优化和低碳化的努力，以适应环境可持续性和气候变化的挑战。

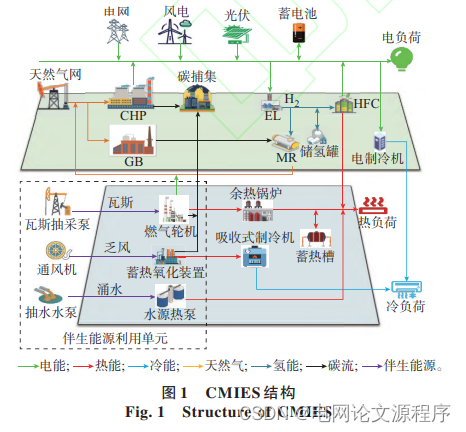
仿真算例：为验证本文所提含伴生能源和 CCS-P2G 耦合 的 CMIES 低碳经济调度模型的有效性，以云南某大 型煤矿为例，且该矿区周边还建有风力发电厂和光伏电站，CMIES 耦合结构如图 1 所示。矿区风光及 负荷预测出力如附录 B 图 B1 所示，煤矿某经典日下 的瓦斯、乏风、涌水流量与浓度分别如图 B2 至图 B4 所示。各设备参数如附录 C 表 C1 所示，所采用的分 时电价如表 C2 所示，弃风、弃光、弃伴生能源惩罚系 数如表 C3 所示。为 验 证 CMIES 中 考 虑 伴 生 能 源 利 用 及 P2GCCS 协同运行的经济与环境效益，设置以下 4 个场 景进行分析。 场景 1：不考虑伴生能源利用，不含 CCS、P2G。 场 景 2：不 考 虑 伴 生 能 源 利 用 ，含 CCS、传 统 P2G。 场景 3：考虑伴生能源利用，含 CCS、传统 P2G。 场 景 4：考 虑 伴 生 能 源 利 用 ，含 CCS、两 段 式 P2G。 如上所述，对设置的 4 种场景进行仿真分析，其 优化调度结果如表 1 所示。

仿真程序复现思路：

为了复现和验证文章中提到的CMIES低碳经济调度模型，需要采取以下步骤：

1. 建立基本模型结构： 根据图1中的CMIES结构，以及文章中的描述，建立相应的数学模型。这可能包括考虑能源生产、传输、储存和使用的各个环节，以及优化目标函数和约束条件。

2. 数据准备：

   • 利用附录B中的图B1至图B4的数据，包括风光和负荷的预测出力，瓦斯、乏风、涌水流量与浓度等。
   • 使用附录C中的表C1至表C3中的设备参数、分时电价以及弃风、弃光、弃伴生能源惩罚系数等信息。

3. 编写仿真代码：

   • 使用合适的编程语言（如Python、MATLAB等）编写仿真代码。
   • 实现CMIES模型的数学表达，包括目标函数和约束条件。
   • 利用数据进行仿真，模拟矿区的能源调度情况。

4. 验证不同场景的仿真结果：

   • 设置场景1至场景4，即不同的能源利用和技术组合情况，分别运行仿真模型。
   • 比较不同场景下的优化调度结果，包括经济和环境效益。

下面是一个简化的Python伪代码，展示了如何开始编写仿真代码：

import numpy as np
from scipy.optimize import minimize

# 假设的数据集
# 风力发电、光伏发电和煤矿发电的预测出力
wind_power_forecast = [100, 150, 120, 90, 80]  # 示例数据
solar_power_forecast = [80, 100, 110, 90, 85]  # 示例数据
coal_power_forecast = [200, 180, 210, 190, 195]  # 示例数据

# 其他参数
electricity_price = [0.1, 0.12, 0.11, 0.13, 0.1]  # 不同时间点的电价
penalty_factors = {'wind': 0.05, 'solar': 0.04, 'coal': 0.06}  # 弃能源惩罚系数

# 定义能源调度模型
def energy_dispatch(variables):
    # variables: [wind_power_to_grid, solar_power_to_grid, coal_power_to_grid]

    wind_power_to_grid, solar_power_to_grid, coal_power_to_grid = variables

    # 计算总成本（这里简化为电力成本）
    total_cost = (
        wind_power_to_grid * electricity_price[0] +
        solar_power_to_grid * electricity_price[1] +
        coal_power_to_grid * electricity_price[2]
    )

    # 计算弃能源的惩罚成本
    wind_penalty = max(0, wind_power_forecast[0] - wind_power_to_grid) * penalty_factors['wind']
    solar_penalty = max(0, solar_power_forecast[0] - solar_power_to_grid) * penalty_factors['solar']
    coal_penalty = max(0, coal_power_forecast[0] - coal_power_to_grid) * penalty_factors['coal']
    total_penalty = wind_penalty + solar_penalty + coal_penalty

    # 目标函数：最小化总成本
    total_objective = total_cost + total_penalty

    return total_objective

# 定义约束条件
constraints = ({'type': 'ineq', 'fun': lambda x: x[0] - wind_power_forecast[0]},  # 风力发电约束
               {'type': 'ineq', 'fun': lambda x: x[1] - solar_power_forecast[0]},  # 光伏发电约束
               {'type': 'ineq', 'fun': lambda x: x[2] - coal_power_forecast[0]})  # 煤矿发电约束

# 初始变量值
initial_guess = [50, 60, 70]  # 随机初始值

# 优化求解
result = minimize(energy_dispatch, initial_guess, constraints=constraints)

# 输出结果
print("Optimal solution (Wind, Solar, Coal):", result.x)
print("Optimal total cost:", result.fun)

这个示例代码中，我们建立了一个简化的能源调度模型，考虑了风力发电、光伏发电、煤矿发电和弃能源的惩罚成本，并设定了约束条件。最后，利用scipy.optimize库中的minimize函数求解了这个优化问题，并输出了最优解和对应的最小总成本。

请注意，这只是一个非常简化的示例，实际情况可能更为复杂，需要更多的数据处理、模型优化和算法调节。建议根据具体情况和实际需求进一步完善和调整代码。