目录
1.任务概述
2.编码器-解码器
3.跳跃连接
4.实现细节
5.损失函数
6.上采样方法
不填充还是填充?
7.U-Net 的运作方式
8.结论
1.任务概述
U-Net 是为语义分割任务开发的。当神经网络接受图像作为输入时,我们可以选择一般性地分类对象或按实例分类。我们可以预测图像中包含的对象(图像分类),所有对象的位置(图像定位/语义分割),或个别对象的位置(对象检测/实例分割)。
下图显示了这些计算机视觉任务之间的差异。为了简化问题,我们仅考虑一个类别和一个标签的分类。

在分类任务中,我们输出一个大小为 k 的向量,其中 k 是类别的数量。在检测任务中,我们需要输出定义边界框的向量 x、y、高度、宽度、类别。
但在分割任务中,我们需要输出与原始输入具有相同维度的图像。这代表了一个相当大的工程挑战:神经网络如何从输入图像中提取相关特征,然后将它们投影到分割掩模中?
2.编码器-解码器
如果你对编码器-解码器不熟悉,建议你阅读这篇文章:
https://towardsdatascience.com/understanding-latent-space-in-machine-learning-de5a7c687d8d
编码器-解码器之所以相关,是因为它们产生了与我们想要的类似的输出:具有与输入相同维度的输出。我们是否可以将编码器-解码器的概念应用于图像分割?我们可以生成一个一维的二进制掩模,并使用交叉熵损失来训练网络。
我们的网络由两部分组成:编码器从图像中提取相关特征,解码器部分则采用提取的特征并重建分割掩模。
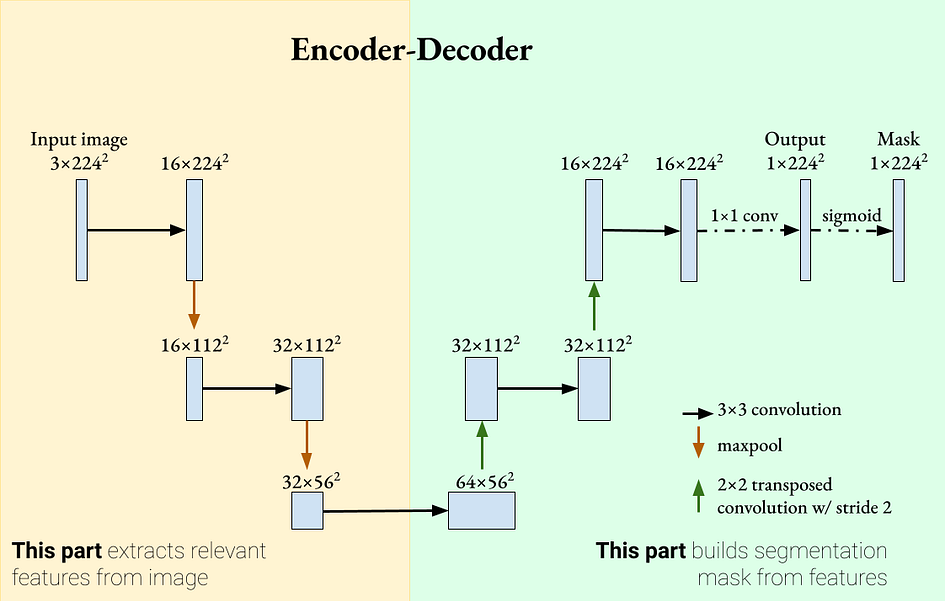
在编码器部分,使用了卷积层,然后使用 ReLU 和最大池作为特征提取器。在解码器部分,使用了转置卷积来增加特征图的大小并减少通道数。使用了填充来保持卷积操作后特征图的大小相同。
你可能注意到的一件事是,与分类网络不同,这个网络没有全连接/线性层。这是一个完全卷积网络(FCN)的示例。FCN已经被证明在分割任务上表现良好,始于Shelhamer等人的论文“全卷积网络用于语义分割”[1]。
然而,这个网络存在一个问题。随着编码器和解码器层的增加,我们实际上会越来越“缩小”特征图。因此,编码器可能会丢弃更详细的特征,以获得更一般的特征。如果我们处理医学图像分割,每个像素被分类为患病/正常可能都很重要。我们如何确保这个编码器-解码器网络接受既有一般性又有详细性的特征?
3.跳跃连接
https://towardsdatascience.com/introduction-to-resnets-c0a830a288a4
由于深度神经网络在通过连续层传递信息时可能“遗忘”某些特征,跳跃连接可以重新引入这些特征,使学习更强大。跳跃连接是在残差网络(ResNet)中引入的,并显示出分类改进以及更平滑的学习梯度。受到这一机制的启发,我们可以将跳跃连接添加到 U-Net 中,以使每个解码器包含其对应编码器的特征图。这是 U-Net 的一个定义特征。
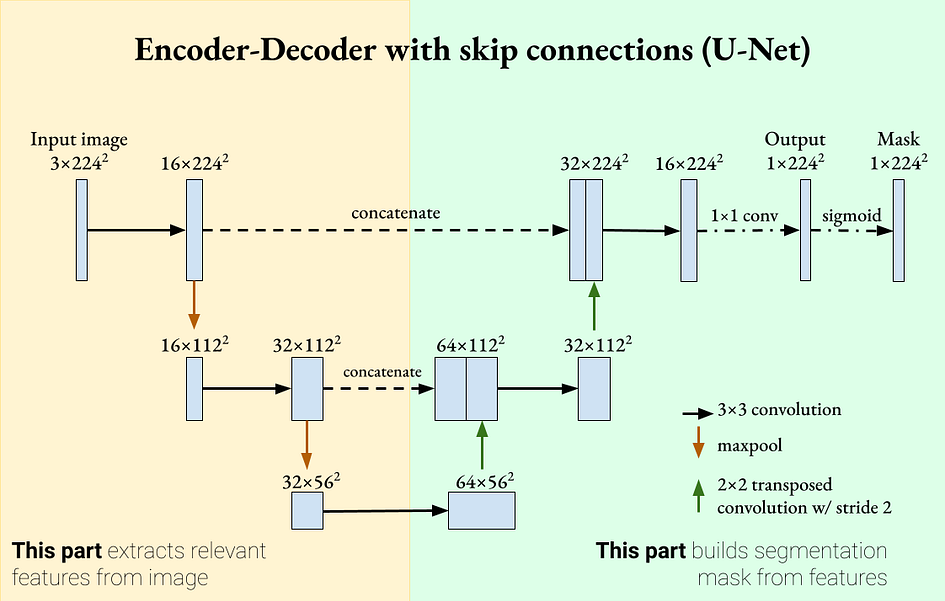
U-Net 是一个带有跳跃连接的编码器-解码器分割网络。作者提供的图片。U-Net 具有两个定义特性:
-
编码器-解码器网络,深入进行时提取更一般性的特征。
-
跳跃连接,重新引入解码器中的详细特征。这两个特性意味着 U-Net 可以使用既详细又一般的特征进行分割。U-Net 最初是为生物医学图像处理引入的,其中分割的准确性非常重要[2]。
4.实现细节

前面的部分提供了 U-Net 的非常一般的概述以及它为什么有效。然而,细节在一般理解和实际实施之间起着重要作用。在这里,我将概述一些 U-Net 的实现选择。
5.损失函数
因为目标是二进制掩模(像素值为1表示像素包含对象),用于将输出与地面实况进行比较的常见损失函数是分类交叉熵损失(或在单标签情况下的二元交叉熵损失)。
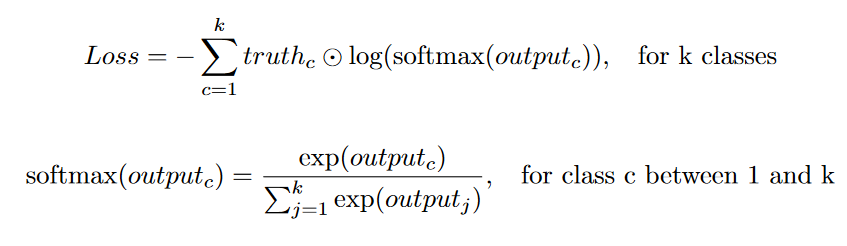
在原始的 U-Net 论文中,额外的权重被添加到损失函数中。这个权重参数有两个作用:它补偿了类别不平衡,并且赋予了分割边界更高的重要性。在我找到的许多 U-Net 实现中,这个额外的权重因子通常没有被使用。
另一个常见的损失函数是 Dice 损失。Dice 损失通过比较两组图像的交集区域与它们的总区域来衡量它们的相似性。请注意,Dice 损失与交并比(IOU)不同。它们衡量了类似的内容,但分母不同。Dice 系数越高,Dice 损失越低。
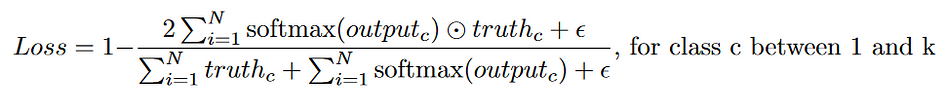
在这里,添加了一个 epsilon 项以避免除以0(epsilon 通常为1)。一些实现,如Milletari等人的实现,在求和之前会将分母中的像素值平方[3]。与交叉熵损失相比,Dice 损失对于不平衡的分割掩模非常鲁棒,这在生物医学图像分割任务中很常见。
6.上采样方法
另一个细节是解码器的上采样方法的选择。以下是一些常见的方法:
双线性插值。该方法使用线性插值来预测输出像素。通常,通过这种方法进行上采样之后会跟随一个卷积层。
最大反池化。这个方法是最大池化的反操作。它使用最大池化操作的索引,并将这些索引填充为最大值。所有其他值设为0。通常,在最大反池化之后会跟随一个卷积层以“平滑”所有缺失的值。
反卷积/转置卷积。有许多关于反卷积的博文。我建议阅读这篇文章作为一个好的视觉指南。
https://towardsdatascience.com/types-of-convolutions-in-deep-learning-717013397f4d
反卷积有两个步骤:首先在原始图像的每个像素周围添加填充,然后应用卷积。在最初的 U-Net 中,使用了一个2x2的转置卷积,步长为2,用于改变空间分辨率和通道深度。
像素重排。这种方法在超分辨率网络中如 SRGAN 中被使用。首先,我们使用卷积将C x H x W特征图转换为(Cr^2) x H x W。然后,像素重排会以马赛克的方式“重排”这些像素,以产生尺寸为C x (Hr) x (Wr)的输出。
不填充还是填充?
卷积层,如果内核大于1x1且没有填充,将产生比输入更小的输出。这对于 U-Net 是个问题。回想一下前面部分中 U-Net 图中,我们将图像的一部分与其解码的部分连接起来。如果我们不使用填充,那么解码后的图像将具有较小的空间尺寸,与编码后的图像相比。
然而,原始的 U-Net 论文没有使用填充。虽然没有给出理由,但我认为这是因为作者不想在图像边缘引入分割错误。相反,他们在连接之前对编码的图像进行了中心裁剪。对于输入尺寸为572 x 572的图像,输出将为388 x 388,损失约为50%。如果要在不填充的情况下运行 U-Net,需要在重叠的图块上多次运行以获取完整的分割图像。
7.U-Net 的运作方式
在这里,我们实现了一个非常简单的类 U-Net 网络,只用于分割椭圆。这个 U-Net 只有3层深度,使用相同的填充,和二元交叉熵损失。更复杂的网络可以在每个分辨率上使用更多的卷积层,或根据需要扩展深度。
import torch
import numpy as np
import torch.nn as nn
class EncoderBlock(nn.Module):
# Consists of Conv -> ReLU -> MaxPool
def __init__(self, in_chans, out_chans, layers=2, sampling_factor=2, padding="same"):
super().__init__()
self.encoder = nn.ModuleList()
self.encoder.append(nn.Conv2d(in_chans, out_chans, 3, 1, padding=padding))
self.encoder.append(nn.ReLU())
for _ in range(layers-1):
self.encoder.append(nn.Conv2d(out_chans, out_chans, 3, 1, padding=padding))
self.encoder.append(nn.ReLU())
self.mp = nn.MaxPool2d(sampling_factor)
def forward(self, x):
for enc in self.encoder:
x = enc(x)
mp_out = self.mp(x)
return mp_out, x
class DecoderBlock(nn.Module):
# Consists of 2x2 transposed convolution -> Conv -> relu
def __init__(self, in_chans, out_chans, layers=2, skip_connection=True, sampling_factor=2, padding="same"):
super().__init__()
skip_factor = 1 if skip_connection else 2
self.decoder = nn.ModuleList()
self.tconv = nn.ConvTranspose2d(in_chans, in_chans//2, sampling_factor, sampling_factor)
self.decoder.append(nn.Conv2d(in_chans//skip_factor, out_chans, 3, 1, padding=padding))
self.decoder.append(nn.ReLU())
for _ in range(layers-1):
self.decoder.append(nn.Conv2d(out_chans, out_chans, 3, 1, padding=padding))
self.decoder.append(nn.ReLU())
self.skip_connection = skip_connection
self.padding = padding
def forward(self, x, enc_features=None):
x = self.tconv(x)
if self.skip_connection:
if self.padding != "same":
# Crop the enc_features to the same size as input
w = x.size(-1)
c = (enc_features.size(-1) - w) // 2
enc_features = enc_features[:,:,c:c+w,c:c+w]
x = torch.cat((enc_features, x), dim=1)
for dec in self.decoder:
x = dec(x)
return x
class UNet(nn.Module):
def __init__(self, nclass=1, in_chans=1, depth=5, layers=2, sampling_factor=2, skip_connection=True, padding="same"):
super().__init__()
self.encoder = nn.ModuleList()
self.decoder = nn.ModuleList()
out_chans = 64
for _ in range(depth):
self.encoder.append(EncoderBlock(in_chans, out_chans, layers, sampling_factor, padding))
in_chans, out_chans = out_chans, out_chans*2
out_chans = in_chans // 2
for _ in range(depth-1):
self.decoder.append(DecoderBlock(in_chans, out_chans, layers, skip_connection, sampling_factor, padding))
in_chans, out_chans = out_chans, out_chans//2
# Add a 1x1 convolution to produce final classes
self.logits = nn.Conv2d(in_chans, nclass, 1, 1)
def forward(self, x):
encoded = []
for enc in self.encoder:
x, enc_output = enc(x)
encoded.append(enc_output)
x = encoded.pop()
for dec in self.decoder:
enc_output = encoded.pop()
x = dec(x, enc_output)
# Return the logits
return self.logits(x)
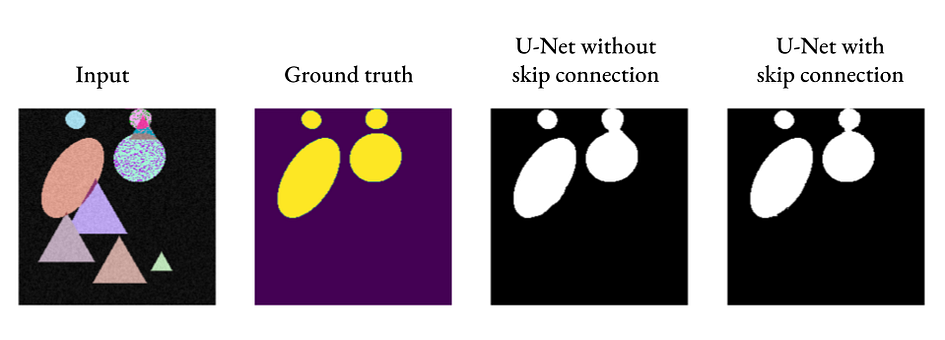
正如我们所看到的,即使没有跳跃连接,U-Net 也可以产生可接受的分割结果,但添加跳跃连接可以引入更精细的细节(请看右侧两个椭圆之间的连接部分)。
8.结论
如果要用一句话来解释 U-Net,那就是 U-Net 就像是用于图像的编码器-解码器,但通过跳跃连接来确保细节不会丢失。U-Net 在许多分割任务中经常使用,近年来还在图像生成任务中取得了成功。