在前一部分我们了解线性表和顺序表概念,如果有不清楚可以参考下面的博客:
数据结构(Chapter Two -01)—线性表及顺序表-CSDN博客
首先列出线性表的数据结构:
#define MaxSize 50 //定义顺序表最大长度
typedef struct{
ElemType data[MaxSize];//顺序表的元素
int length; //顺序表的当前长度
}SqList; //顺序表的类型定义
接下来就是插入、删除、按值查找。
插入
顺序表,我们可以思考数组这一典型的顺序表数据结构,我们需要在第i个位置插入新元素e。
这里定义顺序表为L,基本操作流程就是:
1、判断数据有效性和存储空间是否满,注意了可以插到表尾后一个元素,所以i>L.length+1
2、为第i个位置腾出位置,那就把第i个元素及之后的元素往后移,注意了这是从最后一个元素开始移的。
3、在位置i放入元素e。
代码如下:
bool ListInsert(SqList &L,int i,ElemType e){
if(i<1||i>L.length+1) //判断i的范围是否有效
return false;
if(L.length>=MaxSize)//当前存储空间已满,不能插入
return false;
for(int j =L.length;j>=i;j--)//将第i个元素及之后的元素后移
L.data[j]=L.data[j-1];
L.data[i-1]=e; //在位置i处放e
L.length++; //线性表长度加1
return true;
}最好情况:表尾插入,不需要移,时间复杂度为O(1)
最坏情况:表首插入,需要执行n次移动操作,时间复杂度为O(n)
平均情况:O(n)

删除
删除第i个位置的元素,将删除的值赋给e
操作流程:
1、判断数据有效性
2、将删除的值赋给e
3、将第i+1个元素及后面元素往前移
bool ListDelete(SqList &L,int i,Elemtype &e){
if(i<1||i>L.length) //判断i的范围是否有效
return false;
e = L.data[i-1]; //将删除的元素赋值给e
for(int j=i;j<L.length;j++)//将第i个位置后的元素前移
L.data[j-1]=L.data[j];
L.length--; //线性表长度减1
return true;
}最好情况:删除表尾,不需移,时间复杂度O(1)
最坏情况:删除表首元素,需要移动除表头元素外的所有元素,时间复杂度为O(n)
平均情况:O(n)
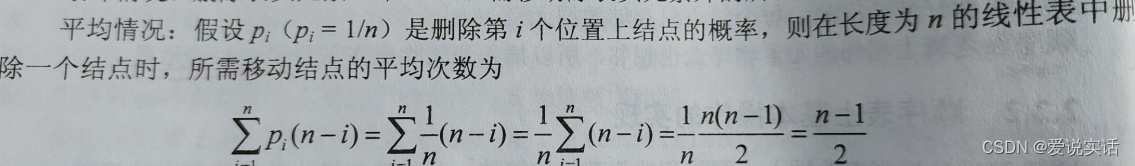
按值查找
查找第一个元素等于e的元素,并放回其位序(位序不等于下标,等于下标+1)
操作流程:
遍历一遍表,当找到第一个符合的就直接放回位序,结束查找
int LocateElem(SqList L,ElemType e){
for(int i =0;i<L.length;i++){//遍历一遍表,当找到第一个符合的就直接放回位序,结束查找
if(L.data[i]==e)
return i+1;
}
return 0;
}最好情况:元素在表头,时间复杂度O(1)
最坏情况:元素在表尾,需要比较n次,时间复杂度O(n)
平均情况:O(n)
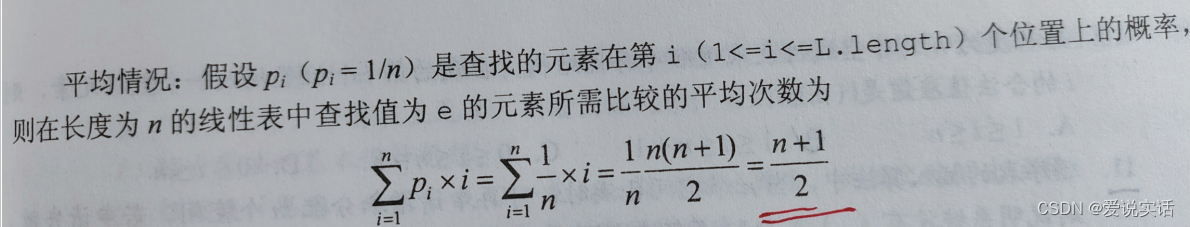
最后,拿着写代码来试一波效果!
#include <stdio.h>
#define MaxSize 20
typedef struct{
int data[MaxSize];
int length=0;
}SqList;
bool ListInsert(SqList &L,int i,int e){
if(i<1||i>L.length+1) //判断i的范围是否有效
return false;
if(L.length>=MaxSize)//当前存储空间已满,不能插入
return false;
for(int j =L.length;j>=i;j--)//将第i个元素及之后的元素后移
L.data[j]=L.data[j-1];
L.data[i-1]=e; //在位置i处放e
L.length++; //线性表长度加1
return true;
}
bool ListDelete(SqList &L,int i,int &e){
if(i<1||i>L.length) //判断i的范围是否有效
return false;
e = L.data[i-1]; //将删除的元素赋值给e
for(int j=i;j<L.length;j++)//将第i个位置后的元素前移
L.data[j-1]=L.data[j];
L.length--; //线性表长度减1
return true;
}
int LocateElem(SqList L,int e){
for(int i =0;i<L.length;i++){//遍历一遍表,当找到第一个符合的就直接放回位序,结束查找
if(L.data[i]==e)
return i+1;
}
return 0;
}
int main()
{
SqList L;
int e = 0;
for(int i=0;i<10;i++){//给顺序表赋值
L.data[i]=10-i;
L.length++;
}
printf("原始顺序表:");
for(int i=0;i<L.length;i++) printf("%d ",L.data[i]);
printf("\n");
ListInsert(L,4,e);//第四个位置加12
printf("增加后顺序表:");
for(int i=0;i<L.length;i++) printf("%d ",L.data[i]);
printf("\n");
ListDelete(L,3,e);//第三个位置删除
printf("删除后顺序表:");
for(int i=0;i<L.length;i++) printf("%d ",L.data[i]);
printf("\n");
printf("查找0的位置:");
int ans = LocateElem(L,0);//查找0的位置
printf("%d",ans);
} 运行结果如下:
最后的最后,可能会有友友对于代码参数里面的"&"会有疑惑?
看一下函数顺序表不加“&”的运行结果: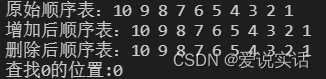
可以看出顺序表没有改变。这个“&”的作用是取地址或者引用,在函数的参数列表里面看到的“&”,通常代表了引用。引用可以看成是变量的别名,它的好处就是避免了复制参数的开销,并且允许函数直接访问和修改原始数据。注意了这个引用是可以修改原始数据的,就是修改main里面的顺序表L。没有引用,虽然完成了函数的流程,但修改不了原始数据表。
看一段代码:
void increment(int &x){
x++;
}
int main(){
int y=5;
increment(y);//y的值由5变成6
}这个里面“&”为引用,当我们调用increment(y)时,我们实际上把y的地址传递到函数,而不是它的值,这样函数可以直接修改y,在函数参数中使用引用时,我们不需要在调用函数中再次使用&符号,因为在定义函数的时候已经定义了该参数需要引用。
可以敲敲代码试一下!