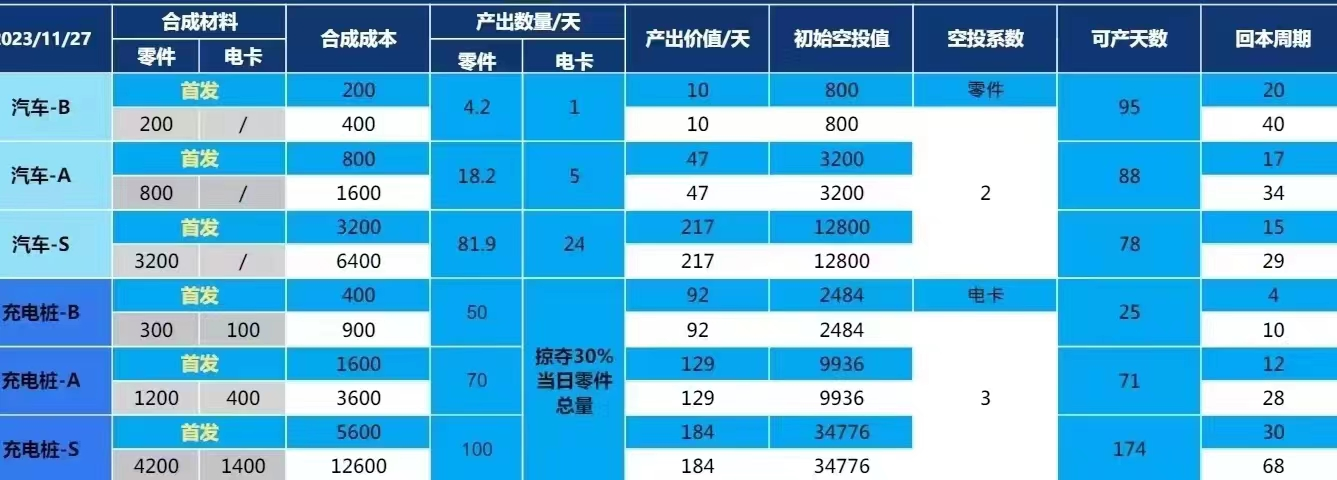
我在大二学习拓扑排序的时候,不是很明白,现在已经大四,抽时间复习一下拓扑排序。
什么是拓扑排序?
如何实现拓扑排序?
拓扑排序的拓展
什么是拓扑排序?
首先拓扑排序的定义如下:
拓扑排序是一种对有向无环图的顶点进行排序的方法。它的主要目的是产生一个顶点的线性序列,使得如果在图中存在一条从顶点 A 指向顶点 B 的边,则在排序结果中,顶点 A 出现在顶点 B 之前。
什么意思呢?我的理解拓扑排序 简单的说,就是 遍历一个没有环的有向图中, 按照箭头的顺序遍历节点。
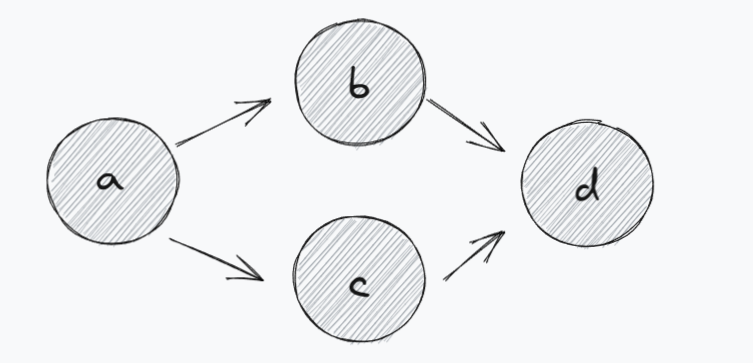
在上面一个有向无环图中,必须先访问a,才可以访问b或c;必须先访问b和c,才可以访问d。
所以,图的拓扑排序为a,b,c,d 或者a,c,b,d
如何实现拓扑排序?
这里我首先给出拓扑排序的算法,只有两步:
第一步:访问一个入度为0的节点
第二步:删除入度为0的节点以及从这个节点出去的所有边,继续执行1,直至图中没有节点。

以上面的图为例,a的入度为0,所以访问a,同时删除a和a的两个出边;此时,b和c节点的入度变为0。

因为b和c的入度都为0,我们可以随便选择一个访问,假设访问的b,删除b节点和它 的出边。

然后访问c节点,删除c节点和它 的出边,此时d节点入度为0,直接删除d节点,图中没有节点;
算法执行完毕。所以一个拓扑排序是 a,b,c,d。
如何来实现呢?我这里直接给出结论:使用BFS进行拓扑排序。
-
计算入度:对于图中的每个顶点,计算它的入度(即有多少边指向该顶点)。
-
初始化队列:创建一个队列,用于存储所有入度为 0 的顶点。这些顶点没有任何先决条件,可以立即处理。
-
拓扑排序:
- 当队列不为空时,从队列中移除一个顶点,并将其添加到拓扑排序的结果中。
- 遍历该顶点的所有邻接顶点,将这些邻接顶点的入度减 1(因为它们的一个依赖已经被移除了)。
- 如果任何邻接顶点的入度变为 0,则将其添加到队列中。
-
检查是否存在拓扑排序:如果排序结果中的顶点数量不等于图中的顶点总数,则说明图中存在环,因此不存在拓扑排序。
为什么可以使用BFS呢?(BFS算法不在这里多讲了。)
BFS 以层级的方式遍历,在处理当前层的顶点之前,所有的前置顶点(即入度已被减至 0 的顶点)已经被处理。这种层级性保证了拓扑排序的正确性。
伪代码:

下面举一个具体的题目,leetcode207. 课程表

class Solution {
public:
bool canFinish(int n, vector<vector<int>>& p) {
vector<int>d(n,0);
vector<vector<int>>g(n);
for(int i=0;i<p.size();i++){
g[p[i][0]].push_back(p[i][1]);
d[p[i][1]]++;
}
queue<int>q;
int cnt=0;
for(int i=0;i<n;i++)if(d[i]==0)q.push(i);
while(!q.empty()){
int t=q.front();
q.pop();
cnt++;
for(auto ne:g[t]){
d[ne]--;
if(d[ne]==0)q.push(ne);
}
}
return cnt==n;
}
};上面代码使用C++来实现伪代码的功能,具体过程就不写了,和C++的语法有关系。
拓扑排序的拓展
拓扑排序的一个典型应用是解决具有依赖关系的任务调度问题。例如,在编译器中对程序模块进行编译时,必须先编译依赖模块,这种依赖关系就可以通过拓扑排序来解决。
For example, suppose foo.c calls functions in libx.a and libz.a that call functions in liby.a. Then libx.a and libz.a must precede liby.a on the command line:
unix> gcc foo.c libx.a libz.a liby.a
Libraries can be repeated on the command line if necessary to satisfy the dependence requirements. For example, suppose foo.c calls a function in libx.a that calls a function in liby.a that calls a function in libx.a. Then libx.a must be repeated on the command line:
unix> gcc foo.c libx.a liby.a libx.a
摘自CSAPP
在编译过程中,模块间的依赖关系可以被视为一个有向图,其中每个模块代表一个顶点,依赖关系表示为有向边。例如,如果模块 A 依赖于模块 B,则会有一条从 B 指向 A 的边。
对于CSAPP的例子中,可以使用图来表示这个依赖关系:
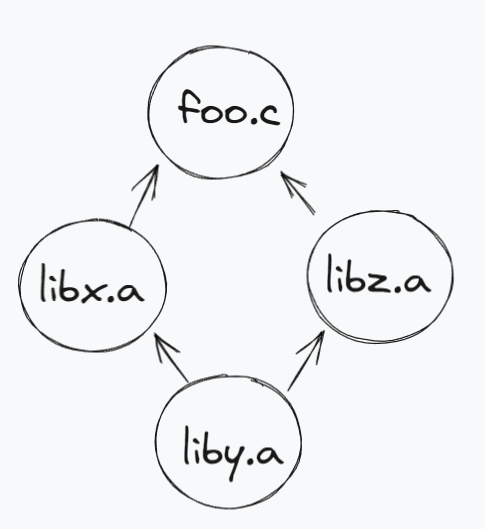
拓扑排序还有一个重要的用途是检测循环依赖。如果模块间的依赖关系形成了一个环,那么将无法进行有效的拓扑排序。这在编译过程中是一个关键的检查点,因为循环依赖通常是编程错误。