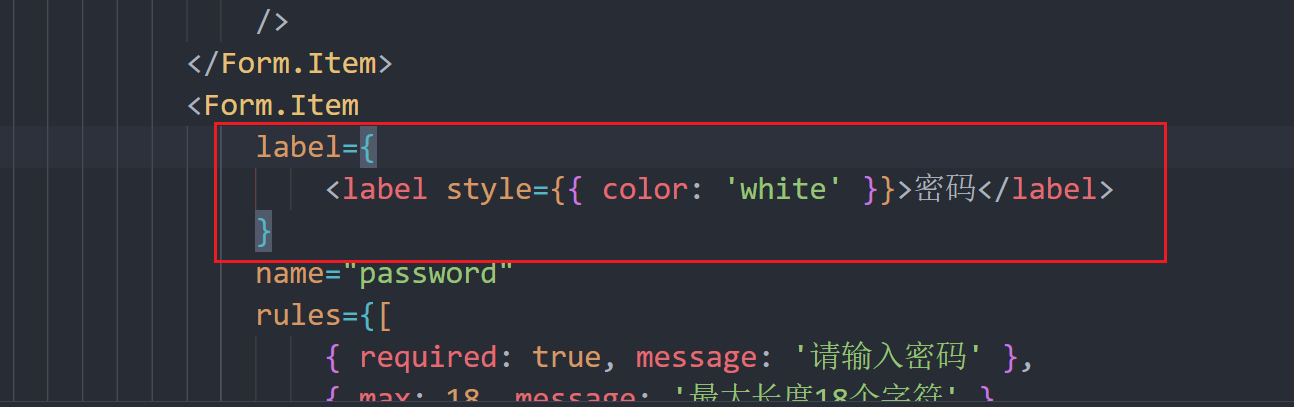
前言
当前电脑的gcc版本为8.3.0,但是在编译其他依赖包的时候,出现各种奇怪的问题,会莫名其妙的中断编译。本地文章讲解如何自编译安装gcc,替换系统自带的gcc。
环境准备
- 下载页面:龙芯开源社区网站 - LoongArch GCC 8.3 交叉工具链 - 源码下载
- 源码包名称如:
loongson-gnu-toolchain-8.3-src-loongarch64-linux-gnu-rc1.2.tar
开始编译
1、解压压缩包
tar -xvf
loongson-gnu-toolchain-8.3-src-loongarch64-linux-gnu-rc1.2.tar
目录结构:

2、解压gcc
tar -xvf gcc-8.3.0-a812acc180.tar.xz
3、下载 GMP, MPFR, MPC, ISL 库源码
编译 GCC 依赖于以上四种库。用户在编译 GCC 之前,将它们的源码路径链接到 GCC 源码目录中即可识别。 这些库最终均静态链接到 GCC 二进制中。 用户可直接使用 GCC 源码中提供的 download_prerequisites 脚本,从