目录
1.树的最长路径
2.树的中心
3.数字转换
4.二叉苹果树
5.战略游戏
6.皇宫守卫
树形DP是一种动态规划方法,主要用于解决树形结构的问题。在树形DP中,通常会使用动态规划的思想来求解最优化问题。其核心在于通过不断地分解问题和优化子问题来解决原问题,以达到提高效率的目的。
树形DP的实现通常会使用递归或迭代的方式,其中递归的方式较为直观,而迭代的方式则可以避免递归可能导致的栈溢出问题。
在树形DP中,通常会使用状态转移方程来描述子问题与原问题之间的关系,以及如何从子问题的解推导出原问题的解。通过不断地优化子问题,最终可以求解出原问题的解。
需要注意的是,树形DP的问题通常涉及到很多细节,需要注重细节的处理,避免因为粗心大意而犯错。同时,在训练过程中,要勤于总结自己的经验和教训,不断完善自己的知识体系。
想法:
任取一个点作为起点,找到距离该点最远的一个点u。
再找到距离u最远的一点v。DFS、BFS。
1.树的最长路径
给定一棵树,树中包含n个结点(编号1~n)和n-1条无向边,每条边都有一个权值。
现在请你找出树中的一条最长路径。
换句话说,要找到两个点,使得它们的距离最远。
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 10010, M = N * 2;
int n;
int h[N], e[M], w[M], ne[M], idx;
int ans;
void add(int a, int b, int c)
{
e[idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx++;
}
int dfs(int u, int father)
{
int dis = 0;//表示当前往下走的最大长度
int d1 = 0, d2 = 0;
for(int i = h[u];i != 1; i = ne[i])
{
int j = e[i];
if(j == father) continue;
int d = dfs(j, u) + w[i];
dist = max(dist, d);
if(d >= d1)
{
d2 = d1;
d1 = d;
}
else if(d > d2)
{
d2 = d;
}
}
ans = max(ans, d1 + d2);
return dist;
}
int main()
{
cin >> n;
memset(h, 0, sizeof(h));
for(int i = 0;i < n - 1; i++)
{
int a, b, c;
cin >> a >> b >> c;
add(a, b ,c); add(b, a, c);
}
dfs(1, -1);
cout << ans << endl;
return 0;
}2.树的中心
给定一棵树,树中包含n个结点(编号1~n)和n-1条无向边,每条边都有一个权值。
请你在树中找到一个点,使得该点到树中其它结点的最远距离最近。
输入格式
第一行包含整数n。
接下来n-1行,每行包含三个整数ai,bi,ci,表示点ai和bi之间存在一条权值为ci的边。
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 10010, M = N * 2, INF = 0x3f3f3f3f;
int n;
int h[N], e[M], w[M], ne[M], idx;
int d1[N], d2[N], p1[N], p2[N], up[N];
void add(int a, int b, int c)
{
e[idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx++;
}
int dfs_d(int u, int father)
{
d1[u] = d2[u] = -INF;
for(int i = h[u];i != -1; i = ne[i])
{
int j = e[i];
if(j == father) continue;
int d = dfs_d(j, u) + w[i];
if(d >= d1[u])
{
d2[u] = d1[u];
d1[u] = d;
p2[u] = p1[u];
p1[u] = j;
}
else if(d > d2[u])
{
d2[u] = d;
p2[u] = j;
}
}
if(d1[u] == -INF) d1[u] = d2[u] = 0;
return d1[u];
}
void dfs_u(int u, int father)
{
for(int i = h[u];i != -1; i = ne[i])
{
int j = e[i];
if(j == father) continue;
if(p1[u] == j) up[j] = max(up[u], d2[u]) + w[i];
else up[j] = max(up[u], d1[u]) + w[i];
dfs_u(j, u);
}
}
int main()
{
cin >> n;
memset(h, -1, sizeof(h));
for(int i = 0;i < n - 1; i++)
{
int a, b, c;
cin >> a >> b >> c;
add(a, b, c), add(b, a, c);
}
dfs_d(1, -1);
dfs_u(1, -1);
int res = INF;
for(int i = 1;i <= n; i++)
res = min(res, max(d1[i], up[i]));
printf("%d\n", res);
return 0;
}3.数字转换
如果一个数z的约数之和y(不包括它本身)比它本身小的,那么z就可以变成y,有也可以变成x。
例如4可以变成3,1也可以变为7。
限定所有数字变换在不超过n的正整数范围内进行,求不断进行数字变化且不出现重复数字最多变换步数。
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 50010;
int n;
int h[N], e[N], ne[N], idx;
int sum[N];
bool st[N];
int ans;
void add(int a, int b)
{
e[idx] = b;
ne[idx] = h[a];
h[a] = idex++;
}
void dfs(int u)
{
int d1 = 0, d2 = 0;
for(int i = h[u];i != -1; i = ne[i])
{
int j = e[i];
int d = dfs(j) + 1;
if(d >= d1)
{
d2 = d1;
d1 = d;
}
else if(d >= d2)
{
d2 = d;
}
}
ans = max(ans, d1 + d2);
}
int main()
{
cin >> n;
for(int i = 1;i <= n; i++)
for(int j = 2;j <= m / i; j++)
sum[i + j] += i;
memset(h, -1, sizeof(h));
for(int i = 2;i <= n; i++)
if(i > sum[i])
{
add(sum[i], i);
st[i] = true;
}
for(int i = 1;i <= n; i++)
if(!st[i])
dfs(i);
cout << ans << endl;
return 0;
}4.二叉苹果树
有一棵二叉苹果树,如果树枝有分叉,一定是分二叉,即没有只有一个儿子在的结点
这棵树共有N个结点,编号为1至N,树根编号一定为1.
我们用一棵树枝两端连接的节点编号描述一根树枝的位置。
一棵苹果树的树枝实在是太多了,需要剪枝,但是一些树枝上长有苹果,给定需要保留的树枝数量,求最多能留下多少个苹果。
这里的保留是指最终与1号点连通。
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 110, M = N * 2;
int n, m;
int h[a], e[M], ne[M],w[M], idx;
int f[N][N];
void add(int a, int b, int c)
{
e[idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx++;
}
void dfs(int u, int father)
{
for(int i = h[u];i != -1; i = ne[i])
{
if(j == father) continue;
dfs(e[i], u);
for(int j = m;j >= 0; j--)
for(int k = 0;k < j; k++)
f[u][j] = max(f[u][j], f[u][j - k + 1] + f[e[i]][k] + w[i])
}
}
int main()
{
cin >> n >> m;
for(int i = 1;i < n - 1; i++)
{
int a, b, c;
cin >> a >> b >> c;
add(a, b, c), add(b, a, c);
}
dfs(1, -1);
cout << f[1][m] << endl;
return 0;
}5.战略游戏
鲍勃喜欢玩电脑游戏,特别是战略游戏,但有时他找不到解决问题的方法,这让他很伤心。
现在他有以下问题。
他必须保护一座中世纪城市,这条城市的道路构成了一棵树。
每个节点上的士兵可以观察到所有和这个点相连的边。
他必须在节点上放置最少数量的士兵,以便他们可以观察到所有的边。
你能帮助他吗?
例如,下面的树:
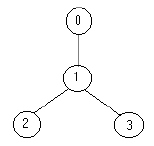
只需要放置 1 名士兵(在节点 1 处),就可观察到所有的边。
输入格式
输入包含多组测试数据,每组测试数据用以描述一棵树。
对于每组测试数据,第一行包含整数 N,表示树的节点数目。
接下来 N 行,每行按如下方法描述一个节点。
节点编号:(子节点数目) 子节点 子节点 …
节点编号从 0 到 N−1,每个节点的子节点数量均不超过 10,每个边在输入数据中只出现一次。
没有上司的舞会:每条边上最多选择一点,最大权值。
战略游戏:每条边上最少选择一个点。
动态规划:
-
状态表示f[i,j] j = 0,1
-
集合:所有在以i为根的子树中选,且点i的状态是j的所有选法。
-
属性:Min
-
-
状态计算:
f[i, 0] = min(f[s1, 1] + f[s2, 1] + ....)f[i, 1] = min(min(f[s1, 0], f[s1, 1]) + min(f[s2, 0], f[s2, 1]) + ....)
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 1510;
int n;
int h[N], e[N], ne[N], idx;
int f[N][2];
bool st[N];
void add(int a, int b)
{
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
void dfs(int u)
{
f[u][0] = 0;
f[u][1] = 1;
for(int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
dfs(j);
f[u][0] += f[j][1];
f[u][1] += min(f[j][0], f[j][1]);
}
}
int main()
{
while(scanf("%d", &n) == 1)
{
memset(h, -1, sizeof(h));
idx = 0;
memset(st, 0, sizeof(st));
for(int i = 0;i < n; i++)
{
int id, cnt;
scanf("%d:(%d)", &id, &cnt);
while(cnt--)
{
int ver;
scanf("%d", &ver);
add(id, ver);
st[ver] = true;
}
}
int root = 0;
while(st[root]) root++;
dfs(root);
printf("%d\n", min(f[root][0], f[root][1]));
}
return 0;
}6.皇宫守卫
太平王世子事件后,陆小凤成了皇上特聘的御前一品侍卫。
皇宫以午门为起点,直到后宫嫔妃们的寝宫,呈一棵树的形状,某些宫殿间可以互相望见。
大内保卫森严,三步一岗,五步一哨,每个宫殿都要有人全天候看守,在不同的宫殿安排看守所需的费用不同。
可是陆小凤手上的经费不足,无论如何也没法在每个宫殿都安置留守侍卫。
帮助陆小凤布置侍卫,在看守全部宫殿的前提下,使得花费的经费最少。
输入格式
输入中数据描述一棵树,描述如下:
第一行 n,表示树中结点的数目。
第二行至第 n+1 行,每行描述每个宫殿结点信息,依次为:该宫殿结点标号 i,在该宫殿安置侍卫所需的经费 k,该结点的子结点数 m,接下来 m 个数,分别是这个结点的 m 个子结点的标号 r1,r2,…,rm。
对于一个 n 个结点的树,结点标号在 1 到 n 之间,且标号不重复。
树形DP
f[ N ] [ 3 ],表示3种状态: 0 表示父节点放了守卫, 1 表示子节点放了守卫, 2 表示自身放了守卫
则f[ u ] [ 0 ] += min(f[ j ] [ i ], f[ j ] [ 2 ]) 父节点放了守卫, 那么它的字节点可放可不放,我们取最小值
f[ u ] [ 2 ] += min(f[ j ] [ 0 ], min(f[ j ] [ 1 ], f[ j ] [ 2 ])) 自身放了守卫, 子节点可放可不放, 去3种状态的最小值
思考子节点放了守卫的情况:
枚举哪个子节点放了守卫, 即f[j ] [ 2 ], 其他子节点可放可不放, 可以先用sum求出子节点值的总和, 即f[ u ] [ 0 ],**
f[ u ] [ 0 ] - min(f[ j ] [ 1 ], - f[ j ] [ 2 ]) 表示去掉j这个子节点其他子节点的总和;
推出:f[ u ] [ 1 ] = min(f[ u ] [ 1 ], f[ j ] [ 2 ] + f[ u ] [ 0 ] - min(f[ j ] [ 1 ], f[ j ] [ 2 ]));
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1510;
int n;
int h[N], e[N], ne[N], idx, w[N];
int f[N][3];
bool st[N];
void add(int a, int b)
{
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
void dfs(int u)
{
f[u][2] = w[u];
for(int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
dfs(j);
f[u][0] += min(f[j][1], f[j][2]);
f[u][2] += min(min(f[j][0], f[j][1]), f[j][2]);
}
f[u][1] = 1e9;
for(int i = h[u]; ~i; i= ne[i])
{
int j = e[i];
f[u][1] += min(f[i][1], f[j][2] + f[u][0] - min(f[j][1], f[j][2]));
}
}
int main()
{
cin >> n;
memset(h, -1, sizeof(h));
for(int i = 1;i <= n; i++)
{
int id, cost, cnt;
cin >> id >> cost >> cnt;
w[id] = cost;
while(cnt--)
{
int ver;
cin >> ver;
add(id, ver);
st[ver] = true;
}
}
int root = 1;
while(st[root]) root++;
dfs(root);
cout << min(f[root][1], f[root][2]) << endl;
return 0;
}