CAD 算法是计算机辅助设计的算法，几何算法是解决几何问题的算法

CAD 算法是指在计算机辅助设计软件中使用的算法，用于实现各种设计和绘图功能，CAD 广泛应用于建筑、机械、电子等领域，可以大大提高设计效率和精度

绘图算法是 CAD 软件的基础，它包括点、线、圆、曲线、等基本图形绘制方法。

DDA (Digital Differential Analyzer)算法是一种在计算机图形学中常用的直线生成算法。这个算法主要思想是通过计算直线斜率来确定每个像素点的位置，从而绘制出一条直线。在 CAD （计算机辅助设计）中，DDA 算法常被用来绘制直线。

算法步骤

• 输入直线的起点 $(x_1,y_1)$ 和终点 $(x_2,y_2)$
• 计算直线的斜率 $k:=\frac{y_2-y_1}{x_2-x_1}$
• 确定步长，如果 $|k|\le 1$ 则以 $x$方向为主轴，步长 为 $\frac{1}{m}$,如果 $|k|>1$则 $y$方向为主轴，步长为 $m$
• 循环绘制，使用步长逐点计算直线上的像素坐标，每个位置绘制像素，直到达到终点

DDA算法是一种简单而有效的直线绘制算法，但有时由于浮点运算的误差，可能导致绘制的直线不够精确。在实际应用中，为了提高精度，可能需要采用其他更复杂的算法，如 Bresenham·算法。

import matplotlib.pyplot as plt

def draw_line_dda(x1, y1, x2, y2):
    dx = x2 - x1
    dy = y2 - y1
    steps = max(abs(dx), abs(dy))

    print(steps, "+++++++++++")

    # 计算步长
    x_increment = dx / steps if steps != 0 else 0  # Avoid division by zero
    y_increment = dy / steps if steps != 0 else 0  # Avoid division by zero

    # 初始化绘制起点
    x = x1
    y = y1

    # 绘制直线
    points = [(x, y)]
    for _ in range(steps):
        x += x_increment
        y += y_increment
        points.append((x, y))

    return points

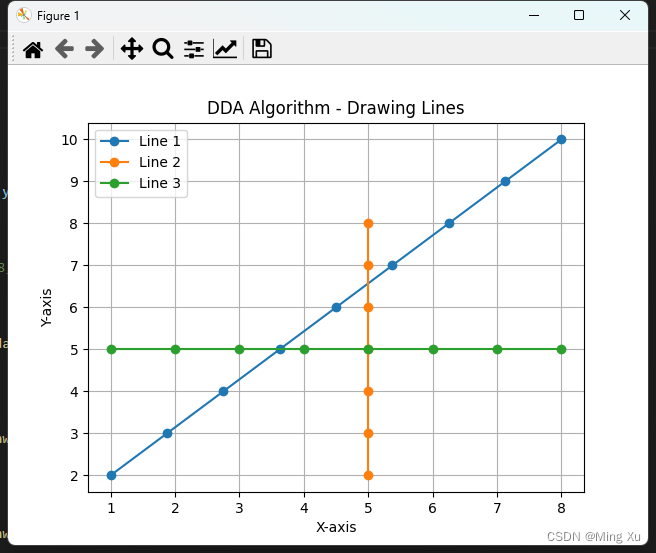
# 示例：绘制直线从(1, 2)到(8, 10)和竖直线从(5, 2)到(5, 8)
x1, y1 = 1, 2
x2, y2 = 8, 10

line_points = draw_line_dda(x1, y1, x2, y2)

x3, y3 = 5, 2
x4, y4 = 5, 8

vertical_line_points = draw_line_dda(x3, y3, x4, y4)

x5, y5 = 1, 5
x6, y6 = 8, 5

hertical_line_points = draw_line_dda(x5, y5, x6, y6)

# 绘制结果
x_values, y_values = zip(*line_points)
plt.plot(x_values, y_values, marker='o', label='Line 1')

x_values, y_values = zip(*vertical_line_points)
plt.plot(x_values, y_values, marker='o', label='Line 2')

x_values, y_values = zip(*hertical_line_points)
plt.plot(x_values, y_values, marker='o', label='Line 3')

plt.title('DDA Algorithm - Drawing Lines')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.legend()
plt.grid(True)
plt.show()