BN的计算公式

BN中均值与方差的计算

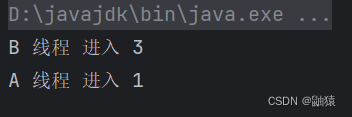
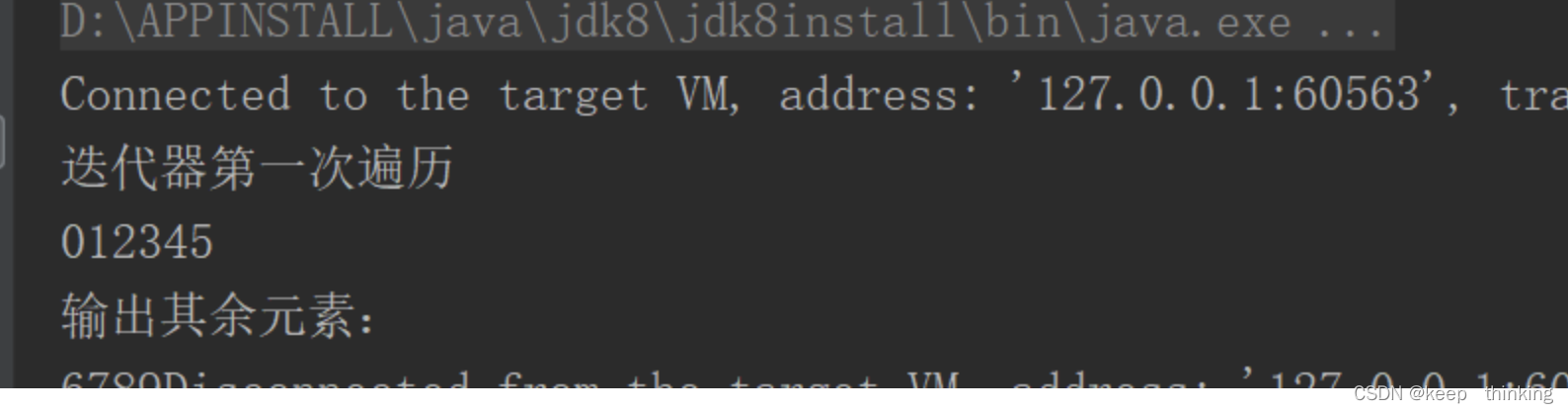
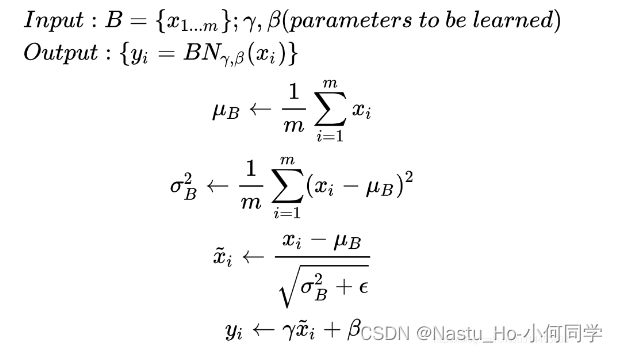所以对于输入x: b,c,h,w
则 mean: 1,c,1,1
	var: 1,c,1,1

代码

class BatchNorm(nn.Module):
    def __init__(self, num_features, num_dims):
        # num_features：完全连接层的输出数量或卷积层的输出通道数。
        # num_dims：2表示完全连接层，4表示卷积层    
        super().__init__()
        if num_dims == 2:
            shape = (1, num_features)
        else:
            shape = (1, num_features, 1, 1)
        # 参与求梯度和迭代的拉伸和偏移参数，分别初始化成1和0
        self.gamma = nn.Parameter(torch.ones(shape))
        self.beta = nn.Parameter(torch.zeros(shape))
        # 非模型参数的变量初始化为0和1
        self.moving_mean = torch.zeros(shape)
        self.moving_var = torch.ones(shape)
 
    def forward(self, x, momentum=0.9, eps=1e-5):
        if self.training:
            assert len(x.shape) in (2, 4)
            #判断是全连接层还是卷积层，2代表全连接层，样本数和特征数；4代表卷积层，批量数，通道数，高宽
            if len(x.shape) == 2:
                # 使用全连接层的情况，计算特征维上的均值和方差
                mean = x.mean(dim=0, keepdim=True)
                var = x.var(dim=0, keepdim=True)
            else:
                # 使用二维卷积层的情况，计算通道维上（axis=1）的均值和方差。
                mean = x.mean(dim=(0, 2, 3), keepdim=True)  # 1, c, 1, 1
                var = x.var(dim=(0, 2, 3), keepdim=True)

            # 训练模式下，用当前的均值和方差做标准化
            x_hat = (x - mean) / torch.sqrt(var + eps)
            # 更新移动平均的均值和方差
            self.moving_mean = momentum * self.moving_mean + (1.0 - momentum) * mean
            self.moving_var = momentum * self.moving_var + (1.0 - momentum) * var
        
        else:
            x_hat = (x - self.moving_mean) / torch.sqrt(self.moving_var + eps)

        out = self.gamma * x_hat + self.beta
        return out