直接插入排序

直接插入排序（Straight InsertionSort）是一种最简单的排序方法，其基本操作是将一条记录插入到已排好的有序表中，从而得到一个新的、记录数量增1的有序表。

原理

通过构建有序序列，对于未排序的数据，在已排序的序列中从后向前遍历，找到相应位置并插入。

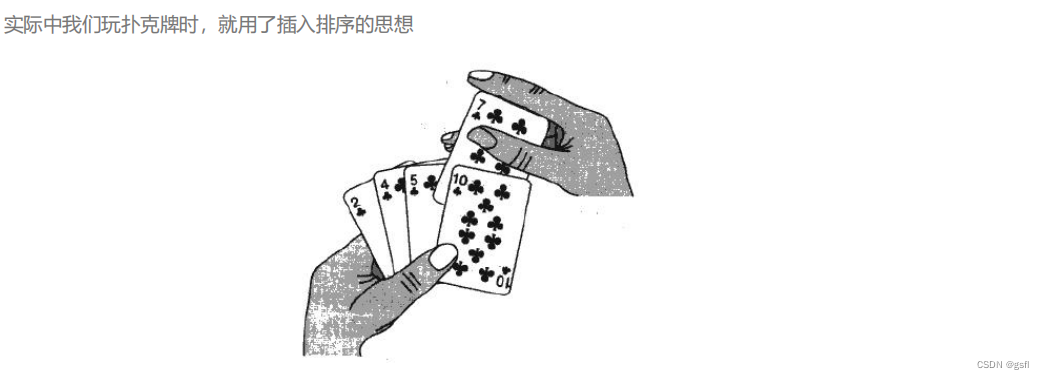
步骤

1.将第一个元素设为已排序
2.对于每个未排序的元素x
a.提取x
b.将x到已排序的元素中从后向前遍历
c.如果当前元素y＞x，y后移一位。反之找到x的正确位置，跳出循环
d.在此插入x的值

视频演示

代码实现

void insertsort(int* a, int n)
{
	for (int i = 0; i < n - 1; i++)
	{
		int x = i;
		int tmp = a[x + 1];
		while (x >= 0)//将要插入的元素到首元素进行遍历
		{
			if (tmp<a[x])//不要用a[x+1]和a[x]比较，因为x再变化，而要x在插入前不变，这个循环为了找到要找到x的位置
			{
				a[x + 1] = a[x];
				x--;
			}
			else
			{
				break;
			}
		}//while循环找到要插入的元素的正确的位置
		a[x + 1] = tmp;//插入x
	}
}
   

int main()
{
	int a[] = { 33,43,14,35,29,28,38,12,2,16,4,13 };
	int n = sizeof(a) / sizeof(a[0]);
	for (int i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
	insertsort(a, n);
	for (int i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
	return 0;
}

特性

1. 元素集合越接近有序，直接插入排序算法的时间效率越高
2. 时间复杂度：O(N^2)
2. 空间复杂度：O(1)，它是一种稳定的排序算法
3. 稳定性：稳定

• 当用直接插入的升序排序去排一个降序的数组时，每个未排序的数x都要遍历完前面所有有序的数才能找到正确的位置，此时时间复杂度最大，为n^2。而一个直接插入的升序排序去排一个接近升序的数组时，遍历的效率大大提高，时间效率也就越高。

• 排序算法的稳定性的定义：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，A1=A2，且A1在A2之前，而在排序后的序列中，A1仍在A2之前，则称这种排序算法是稳定的；否则称为不稳定的。
  比如将上面直接插入排序代码的tmp<a[x]改成tmp<=a[x]。则两个相等的记录会被交换，此时该排序算法就变得不稳定了。

希尔排序

希尔排序(Shell’s Sort)是插入排序的一种，又称“缩小增量排序”（Diminishing IncrementSort），是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因 D.L.Shell 于 1959 年提出而得名。
希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至 1时，整个文件恰被分成一组，算法便终止。

通过上面的直接插入排序我们了解到：当元素集合越接近有序，直接插入排序算法的时间效率越高。而希尔排序就是将一些无序的数据进行调整，变成接近有序的数据，最后通过直接插入排序来完成排序。

原理

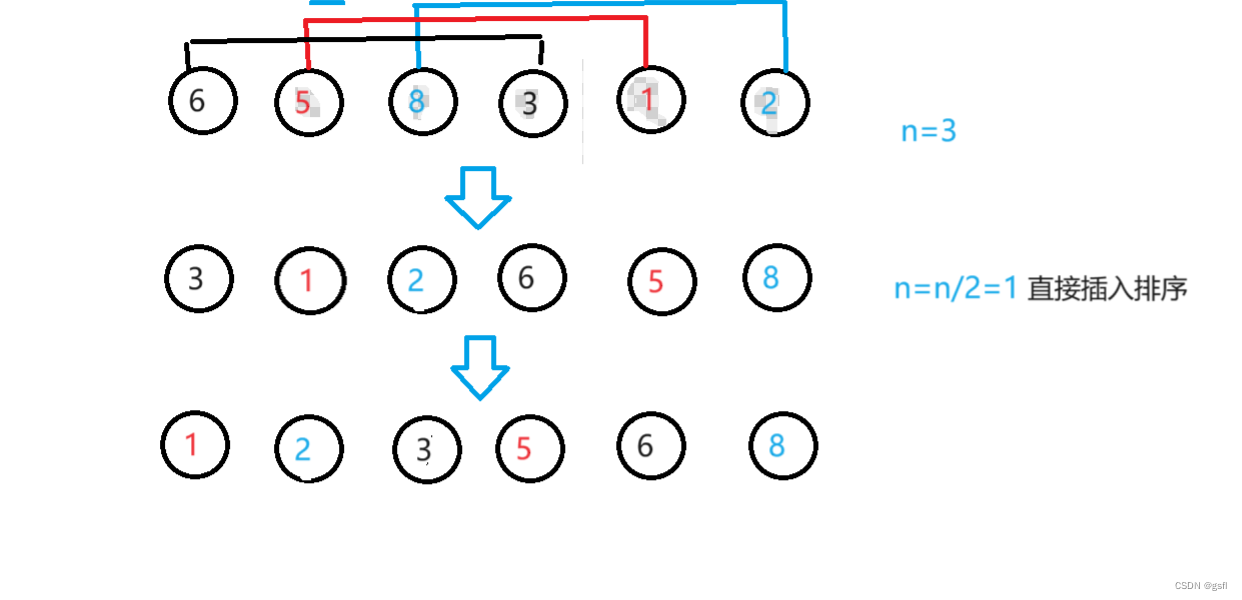
希尔排序的过程可以分为预排序和排序。
进行预排序时，先将原序列分成n个子序列（n为增量，一般为序列长度的一半）然后进行直接插入排序，之后增量取原增量的一半，进行插入排序，直到增量为1时，序列接近有序，再进行一次直接插入排序。

• 希尔排序的增量是希尔在排序算法中提出的一组增量序列，这个增量序列的递推公式是ht=N/2，h[k+1]=h[k]/2，也就是说增量序列是{N/2，(N/2)/2，…，1}。在希尔排序中，使用这个增量序列来分割待排序的数组，并对每个子序列进行插入排序。通过逐渐减小增量，最终使整个数组变得有序。

步骤

1.预排序
a.设置增量序列并进行直接插入排序
b.不断缩小增量重复a，使原序列接近有序
2.排序

图像演示

代码实现

void shellsort(int* a, int n)
{
	int gap = n;
	while (gap>1)
	{
	gap = gap /2;

		for (int i = 0; i < n - gap; i++)//这里每循环一次，代表已完成对一个子序列的排序
		{
			int x = i;
			int tmp = a[x + gap];//当gap为1时就是直接插入排序
			while (x >= 0)
			{
				if (tmp > a[x])
				{
					a[x + gap] = a[x];
					x -= gap;
				}
				else
				{
					break;
				}
			}
			a[x + gap] = tmp;
		}
	}
}


int main()
{
	int a[] = { 33,43,14,35,29,28,38,12,2,16,4,13 };
	int n = sizeof(a) / sizeof(a[0]);
	for (int i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
	/*insertsort(a, n);
	for (int i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}*/
	shellsort(a, n);
	for (int i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
	return 0;
}

希尔排序的分析

《数据结构(C语言版)》-严蔚敏

希尔排序的分析是一个复杂的问题,因为它的时间是所取“增量”序列的函数,这涉及一些数学上尚未解决的难题。因此,到目前为止尚未有人求得一种最好的增量序列,但大量的研究已得出一些局部的结论。如有人指出,当增量序列为dlta[k]=
-1时,希尔排序的时间复杂度为O( n^(3/2) ),其中t为排序趟数,1≤k≤t≤ log₂(n+1)。还有人在大量的实验基础上推出:当n在某个特定范围内,希尔排序所需的比较和移动次数约为
n^1.3,当n→∞时,可减少到n( log₂n)^2[2]。

增量序列可以有各种取法,但需注意:应使增量序列中的值没有除1之外的公因子,并且最后一个增量值必须等于1。

《数据结构-用面相对象方法与C++描述》— 殷人昆
gap 的取法有多种。最初 Shell 提出取 gap =[n/2],gap=[gap/2]直到 gap =1,后来 Knuth 提出取 gop =[gap/3] +1。还有人提出都为好,也有人提出 gap 互质为 好。无论哪一种主张都没有得到证明。
对希尔排序的时间复杂度的分析很困难,在特定情况下可以准确地估算关键码的比较次数和对象移动次数,但想要弄清关键码比较次数和对象移动次数与增量选择之间的依赖关系,并给出完整的数学分析,还没有人能够做到。在Knuth所著的《计算机序设计技巧》第3卷中,利用大量的实验统计资料得出,当n很大时,关键码平均比较次数和对象平均称动次数大约在n^1.25到1.6n^1.25范围内，这是在利用直接插入排序作为子序列排序方法的情况下得到的。

特性

1. 希尔排序是对直接插入排序的优化。
2. 当gap > 1时都是预排序，目的是让数组更接近于有序。当gap == 1时，数组已经接近有序的了，这样就会很快。这样整体而言，可以达到优化的效果。我们实现后可以进行性能测试的对比。
3. 时间复杂度：因为咋们的gap是按照Knuth提出的方式取值的，而且Knuth进行了大量的试验统计，我们暂时就按照n^1.25到1.6n^1.25来算。
4. 稳定性：不稳定

直接插入排序和希尔排序的比较

我们使用clock函数对两种排序的运行时间进行测量并比较，测量排序100000个数据的时间。

int main()
{

	srand(time(0));
	const int N = 100000;
	int* a1 = (int*)malloc(sizeof(int) * N);

	for (int i = 0; i < N; ++i)
	{
		a1[i] = rand();
	}
	int begin1 = clock();
	insertsort(a1, N);
	int end1 = clock();

	int begin2 = clock();
	shellsort(a1, N);
	int end2 = clock();

	printf("insertsort: %d\n", end1 - begin1);
	printf("shellsort: %d\n", end2 - begin2);
	free(a1);
	return 0;
}