SLAM算法与工程实践——SLAM基本库的安装与使用（5）：Ceres优化库

SLAM算法与工程实践系列文章

下面是SLAM算法与工程实践系列文章的总链接，本人发表这个系列的文章链接均收录于此

SLAM算法与工程实践系列专栏

文章目录

SLAM算法与工程实践系列文章
- SLAM算法与工程实践系列文章链接
- SLAM算法与工程实践系列专栏
前言
SLAM算法与工程实践——SLAM基本库的安装与使用（5）：Ceres优化库
- 安装 Ceres
- - 错误
- 使用
- - ceresCurveFitting.cpp
  - 入门介绍
  - - 构建代价函数（STEP2）
    - 1. 定义残差函数
    - 2. 定义优化问题
    - 3. Ceres库的求解器

前言

这个系列的文章是分享SLAM相关技术算法的学习和工程实践

SLAM算法与工程实践——SLAM基本库的安装与使用（5）：Ceres优化库

安装 Ceres

安装参考：

Ubuntu18.04安装Ceres，图文详解

Ubuntu 20.04可以按照官网的方法来安装最新版本，Ubuntu 18.04则要安装老版本的Ceres 1.14.0，见上面的教程

官网：http://ceres-solver.org/

下载源码

You can start with the latest stable release . Or if you want the latest version, you can clone the git repository

git clone https://ceres-solver.googlesource.com/ceres-solver

安装依赖

# CMake
sudo apt-get install cmake
# google-glog + gflags
sudo apt-get install libgoogle-glog-dev libgflags-dev
# Use ATLAS for BLAS & LAPACK
sudo apt-get install libatlas-base-dev
# Eigen3 ，若之前安装过就不用再装了
sudo apt-get install libeigen3-dev
# SuiteSparse (optional)
sudo apt-get install libsuitesparse-dev

编译源码

tar zxf ceres-solver-2.1.0.tar.gz
mkdir ceres-bin
cd ceres-bin
cmake ../ceres-solver-2.1.0
make -j3
make test
# Optionally install Ceres, it can also be exported using CMake which
# allows Ceres to be used without requiring installation, see the documentation
# for the EXPORT_BUILD_DIR option for more information.
sudo make install

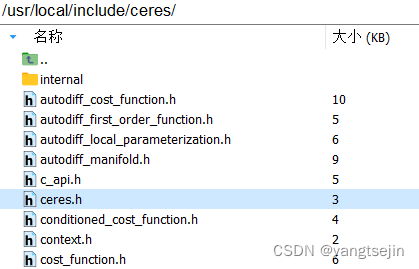
安装完成后，可以在 /usr/local/include/ceres 下找到Ceres的头文件，并在 /usr/local/lib/ 下找到名为 libceres.a 的库文件。如果能找到就代表安装成功了。

在这里插入图片描述

错误

参考：

Using ceres-solver do Bundle Adjustment Runing Crash #428

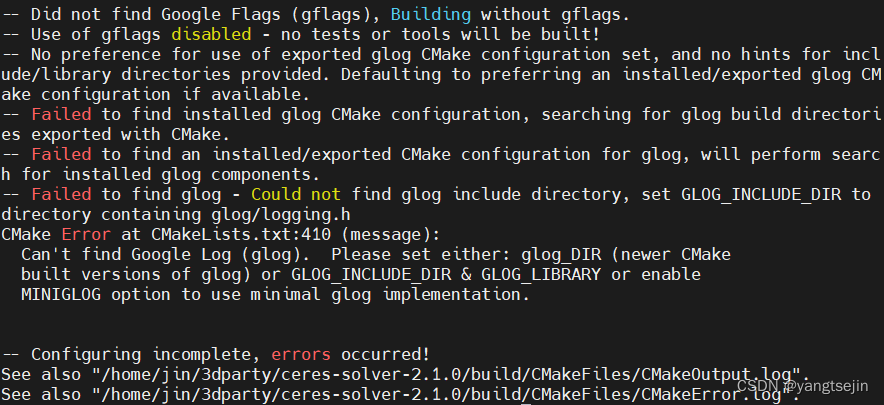
在输入命令 cmake .. 后，报如下错误

-- Failed to find installed glog CMake configuration, searching for glog build directories exported with CMake.
-- Failed to find an installed/exported CMake configuration for glog, will perform search for installed glog components.
-- Failed to find glog - Could not find glog include directory, set GLOG_INCLUDE_DIR to directory containing glog/logging.h
CMake Error at CMakeLists.txt:410 (message):
  Can't find Google Log (glog).  Please set either: glog_DIR (newer CMake
  built versions of glog) or GLOG_INCLUDE_DIR & GLOG_LIBRARY or enable
  MINIGLOG option to use minimal glog implementation.

在这里插入图片描述

使用

参考：

Ceres的Problem::AddParameterBlock()函数

http://ceres-solver.org/nnls_modeling.html#theory

ceresCurveFitting.cpp

这里以 ceresCurveFitting.cpp 为例

首先引入头文件，其中 chrono 库是C++标准库中的一个组件，用于表示和处理时间

详细可见：C++ std::chrono库使用指南 (实现C++ 获取日期,时间戳,计时等功能)

#include <iostream>
#include <opencv2/core/core.hpp>
#include <ceres/ceres.h>
#include <chrono>

进入主函数，首先是随机生成100个加了噪声的点，将其 pushback 进 vector 中

	double ar = 1.0, br = 2.0, cr = 1.0;         // 真实参数值
  double ae = 2.0, be = -1.0, ce = 5.0;        // 估计参数值
  int N = 100;                                 // 数据点
  double w_sigma = 1.0;                        // 噪声Sigma值
  double inv_sigma = 1.0 / w_sigma;
  cv::RNG rng;                                 // OpenCV随机数产生器

  vector<double> x_data, y_data;      // 数据
  for (int i = 0; i < N; i++) {
    double x = i / 100.0;
    x_data.push_back(x);
    y_data.push_back(exp(ar * x * x + br * x + cr) + rng.gaussian(w_sigma * w_sigma));
  }

然后定义了我们要估计的变量，将其存入数组中

	double abc[3] = {ae, be, ce};

接着构建最小二乘问题

	// 构建最小二乘问题
  ceres::Problem problem;
  for (int i = 0; i < N; i++) {
    problem.AddResidualBlock(     // 向问题中添加误差项
      // 使用自动求导，模板参数：误差类型，输出维度，输入维度，维数要与前面struct中一致
      new ceres::AutoDiffCostFunction<CURVE_FITTING_COST, 1, 3>(
        new CURVE_FITTING_COST(x_data[i], y_data[i])
      ),
      nullptr,            // 核函数，这里不使用，为空
      abc                 // 待估计参数
    );
  }

其中 CURVE_FITTING_COST 结构体定义为：

// 代价函数的计算模型
struct CURVE_FITTING_COST {
  CURVE_FITTING_COST(double x, double y) : _x(x), _y(y) {}	// 有参构造，这里的构造函数为空

  // 残差的计算
  template<typename T>
  // 对括号()运算符进行重载，是给Ceres内部求导用的
  bool operator()(
    const T *const abc, // 模型参数，有3维
    T *residual) const {
    residual[0] = T(_y) - ceres::exp(abc[0] * T(_x) * T(_x) + abc[1] * T(_x) + abc[2]); // y-exp(ax^2+bx+c)
    return true;
  }

  const double _x, _y;    // x,y数据
};

关于 AutoDiffCostFunction ，详见：

http://ceres-solver.org/nnls_modeling.html?highlight=autodiffcostfunction#_CPPv4N5ceres20AutoDiffCostFunctionE

配置求解器，用优化库来求解

	// 配置求解器
  ceres::Solver::Options options;     // 这里有很多配置项可以填
  options.linear_solver_type = ceres::DENSE_NORMAL_CHOLESKY;  // 增量方程如何求解
  options.minimizer_progress_to_stdout = true;   // 输出到cout

  ceres::Solver::Summary summary;                // 优化信息
  chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
  ceres::Solve(options, &problem, &summary);  // 开始优化
  chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
  chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
  cout << "solve time cost = " << time_used.count() << " seconds. " << endl;

输出结果

	// 输出结果
  cout << summary.BriefReport() << endl;
  cout << "estimated a,b,c = ";
  for (auto a:abc) cout << a << " ";
  cout << endl;

执行后输出为

在这里插入图片描述

程序中需要说明的地方均已加注释。可以看到，我们利用 OpenCV 的噪声生成器生成了 100 个带高斯噪声的数据，随后利用Ceres进行拟合。这里演示的Ceres用法有如下几项：

定义残差块的类。方法是书写一个类（或结构体），并在类中定义带模板参数的()运算
符，这样该类就成为了一个拟函数(Functor)。这种定义方式使得Ceres可以像调用函数一样，对该类的某个对象（比如 a )调用 a<double>() 方法。事实上，Ceres 会把雅可比矩阵作为类型参数传入此函数，从而实现自动求导的功能。
程序中的 double abc[3] 即参数块，而对于残差块，我们对每一个数据构造 CURVE FITTING COST 对象，然后调用 AddResidualBlock 将误差项添加到目标函数中。由于优化需要梯度，我们有若干种选择：

(1)使用Ceres的自动求导(Auto Diff)；

(2)使用数值求导(Numeric Diff)；

(3)自行推导解析的导数形式，提供给Ceres。因为自动求导在编码上是最方便的，于是我们使用自动求导。
自动求导需要指定误差项和优化变量的维度。这里的误差是标量，维度为1：优化的是 a,b,c 三个量，维度为3。于是，在自动求导 AutoDiffCostFunction 的模板参数中设定变量维度为1、3。
设定好问题后，调用Solve函数进行求解。你可以在 options 里配置（非常详细的）优化选项。例如，可以选择使用 Line Search 还是 Trust Region 、迭代次数、步长，等等。读者可以查看 Options 的定义，看看有哪些优化方法可选，当然默认的配置已经可用于很广泛的问题了。

入门介绍

参考：

http://ceres-solver.org/nnls_modeling.html?highlight=autodiffcostfunction#_CPPv4N5ceres20AutoDiffCostFunctionE

ceres的常见用法总结

优化框架Ceres库用法介绍

ceres库的使用

Ceres-Solver 从入门到上手视觉SLAM位姿优化问题

【SLAM】Ceres优化库超详细解析

Ceres详解（一） Problem类

【SLAM】Ceres优化库官方实例详细解析（SLAM相关问题）

Ceres Solver：从入门到使用

非线性优化器ceres的使用20221125

Ceres库主要用于求解无约束或者有界约束的最小二乘问题。其数学形式如下：
$\begin{aligned}\min_x&\quad\frac12\sum_i\rho_i\left(\|f_i(x_1,\cdots,x_k)\|^2\right)\\\mathrm{s.t.}&\quad l_j\leq x_j\leq u_j\end{aligned}$
我们的任务就是找到一组满足约束 $l_j ≤ x_j ≤ u _j$ 的 $x_1,\cdots,x_k$ ，使得优化目标函数
$\frac{1}{2}\sum_{i}\rho_{i}\left(\|f_{i}\left(x_{1},\cdots,x_{k}\right)\|^{2}\right)$
取值最小

其中的一些变量的解释：

优化参数 $x_1,\cdots,x_k$ ：参数块（ParameterBlock），它们的取值就是我们要寻找的解
$l_j,u_j$ ：第 $j$ 个优化参数 $x_j$ 的下界和上界
表达式 $\rho\big(\|f_i(x_1,\cdots,x_k)\|^2\big)$ ：残差块（ResidualBlock）
$f_i(\cdot)$ ：代价函数（CostFunction）
$\rho_i(\cdot)$ ：损失函数，或者核函数（LossFunction）。它的意义主要是为了降低野点（outliers）对于解的影响

代价函数同时负责计算残差项 ( $f_i(x_1,\cdots,x_k)$ )和雅可比矩阵 $\mathcal{J_i}$
$\mathcal{J}_{i}=\frac{\partial}{\partial x_{i}}f_{i}(x_{1},\cdots,x_{k})\quad\forall i\in1,\cdots,k$
很多时候我们说最小二乘都是拿来做曲线拟合的，实际上只要能够把问题描述成上面的数学形式，就都可以使用Ceres来求解。使用起来也比较简单，只要按照教程介绍的套路，提供代价函数的计算方式，描述清楚每个残差块以及核函数即可。

如下面的示例代码所示，一般我们需要定义三个对象，problem用于描述将要求解的问题，options提供了很多配置项，而summary用于记录求解过程。

ceres::Problem problem;
ceres::Solver::Options options;
ceres::Solver::Summary summary;

Ceres的求解过程包括构建最小二乘和求解最小二乘问题两部分，其中构建最小二乘问题的相关方法均包含在 Ceres::Problem 类中，涉及的成员函数主要包括 Problem::AddResidualBlock() 和 Problem::AddParameterBlock()。

注意：

Ceres Solver 只接受最小二乘优化，也就是 $min r^{T} r$ ；若要对残差加权重，使用马氏距离，即 $min r^{T}P^{-1} r$ ，
则要对信息矩阵 $P^{-1}$ 做Cholesky分解，即 $LL^T=P^{-1}$ ，则 $d=r^T(LL^T)r=(L^Tr)^T(L^Tr)$ ，令 $r'=L^Tr$ ，最终 $min r'^Tr'$

使用 Ceres Solver 求解非线性优化问题，主要包括以下几部分：

构建代价函数(cost function) 或残差(residual)
构建优化问题(ceres::Problem)：通过 AddResidualBlock 添加代价函数(cost function)、损失函数(loss function) 和待优化状态量
- LossFunction: a scalar function that is used to reduce the influence of outliers on the solution of non-linear least squares problems.
配置求解器(ceres::Solver::Options)
运行求解器(ceres::Solve(options, &problem, &summary))

Ceres 使用流程

在这里插入图片描述

使用 Ceres Solver 求解非线性优化问题，主要包括以下几部分：

【STEP 1】构建优化问题（ceres::Problem）

【STEP 2】构建代价函数（ceres::CostFunction）或残差（residual）

【STEP 3】添加代价函数、核函数：通过ceres::Problem::AddResidualBlock添加代价函数（cost function）、核函数（loss function）和输入参数块（即待优化状态量块）

【STEP 4】配置求解器（ceres::Solver::Options）

【STEP 5】运行求解器（ceres::Solve(options, &problem, &summary)）

构建代价函数（STEP2）

在这里插入图片描述

代价函数最重要的功能就是计算残差向量和雅可比矩阵。Ceres提供了三种求导方法，分别是：解析求导、自动求导、数值求导。

在SLAM中，使用的一般都是解析求导，这种方法需要自己填入雅克比函数。

基础代价函数类
先看下最基础的代价函数类的声明：

class CostFunction {
 public:
  virtual bool Evaluate(double const* const* parameters,
                        double* residuals,
                        double** jacobians) const = 0;
  const vector<int32>& parameter_block_sizes();
  int num_residuals() const;

 protected:
  vector<int32>* mutable_parameter_block_sizes();
  void set_num_residuals(int num_residuals);
};

CostFunction的输入参数块的数量和大小以及输出的数量，分别存储在CostFunctio::parameter_block_sizes_和CostFunction::num_residuals_中。从此类继承的子类应使用对应的访问器设置这两个成员。

当使用Problem::AddResidualBlock()添加代价函数时，此信息将由Problem验证。

CostFunction中有一个纯虚函数需要子类进行重写，该纯虚函数的定义为：

bool CostFunction::Evaluate(double const *const *parameters,
						    double *residuals,
						    double **jacobians) const;

纯虚函数的形参的解释：

parameters：输入参数块，大小为parameter_block_sizes_.size()的数组（输入参数块的数量），parameters[i]是大小为parameter_block_sizes_[i]的数组（第i个输入参数块的维度）
residuals：残差，大小为num_residuals_的数组
jacobians：雅可比矩阵，大小为parameter_block_sizes_.size()的数组的数组（输入参数块的数量），jacobians[i]是大小为num_residuals乘parameter_block_sizes_[i的行优先数组（残差对第i个输入参数块求导，即大小为残差维度乘第i个输入参数块维度，再转化为行优先数据组）

jacobians的详细表达式为：
$\text{jacobians}[\mathbf{i}][\mathbf{r}^*\text{parameter block sizes}_-[\mathbf{i}]+\mathbf{c}]=\frac{\partial\text{residual}[r]}{\partial\text{parameters}[i][c]}$
parameters 和 residuals 不能为 nullptr，jacobians 可能为 nullptr。如果 jacobians 为 nullptr，则用户只需计算残差即可。

纯虚函数的返回值指示残差或雅可比的计算是否成功。

1. 定义残差函数

残差函数是用户自定义的模型函数与观测数据之间的误差函数，是Ceres库求解优化问题的重要部分

struct CostFunctor {
  template
  bool operator()(const T* const x, T* residual) const {
    residual[0] = T(10.0) - x[0];
    return true; 
  }
};

以上代码定义了一个求解 x 使得10-x=0 的问题。

2. 定义优化问题

在Ceres库中，优化问题包含一个或多个参数块（Parameter Block）、一个或多个残差函数（Cost Function）、以及优化参数的起始值。在定义优化问题时，需要将所有的优化数据加入到problem对象中。

// 定义优化问题
ceres::Problem problem;

// 添加参数块
double initial_x = 5.0;
double x = initial_x;
problem.AddParameterBlock(&x, 1);

// 添加残差函数
CostFunctor* cost_functor = new CostFunctor;
ceres::CostFunction* cost_function =
   new ceres::AutoDiffCostFunction(cost_functor);
problem.AddResidualBlock(cost_function, nullptr, &x);

// 设置优化参数的起始值
ceres::Solver::Options options;
options.initial_trust_region_radius = 1e-10;

// 求解问题
ceres::Solver::Summary summary;
ceres::Solve(options, &problem, &summary);

3. Ceres库的求解器

Ceres库提供了多种优化问题求解器，包括本地方法（Local Method）和迭代方法（Iterative Method），用户可以根据自己的需要进行选择。

本地方法

Local Parameterization 可以对参数块进行变换，旋转或者平移等，然后在新的参数块上进行非线性优化。

// 定义旋转参数块
double rotation[4] = {1.0, 0.0, 0.0, 0.0};
ceres::LocalParameterization* quaternion_parameterization =
    new ceres::QuaternionParameterization;
problem.AddParameterBlock(rotation, 4, quaternion_parameterization);

// 建立优化问题
ceres::CostFunction* cost_function = new MyCostFunction;
ceres::LossFunction* loss_function = new ceres::HuberLoss(1.0);

// 通过问题中添加参数块
ceres::ResidualBlockId residual_block_id = problem.AddResidualBlock(
    cost_function, loss_function, rotation, translation);

// 求解问题
ceres::Solver::Options options;
ceres::Solver::Summary summary;
ceres::Solve(options, &problem, &summary);

迭代方法

Ceres库提供了多种的迭代方法，如 “L-BFGS-B”, “Trust Region Reflective”, “Dogleg”, “CG” 等，其中每种方法在不同场景下都体现了特殊的优势。

ceres::GradientProblemSolver::Options options;
options.line_search_direction_type = ceres::BFGS;
options.line_search_type = ceres::WOLFE;
options.max_num_iterations = 200;
options.minimizer_progress_to_stdout = true;

ceres::GradientProblemSolver::Summary summary;
ceres::Solve(options, &problem, &summary);