在学习机器学习的过程中,我充分感受到概率与统计知识的重要性,熟悉相关概念思想对理解各种人工智能算法非常有意义,从而做到知其所以然。因此打算写这篇笔记,先好好梳理一下参数估计与假设检验的相关内容。
1 总体梳理
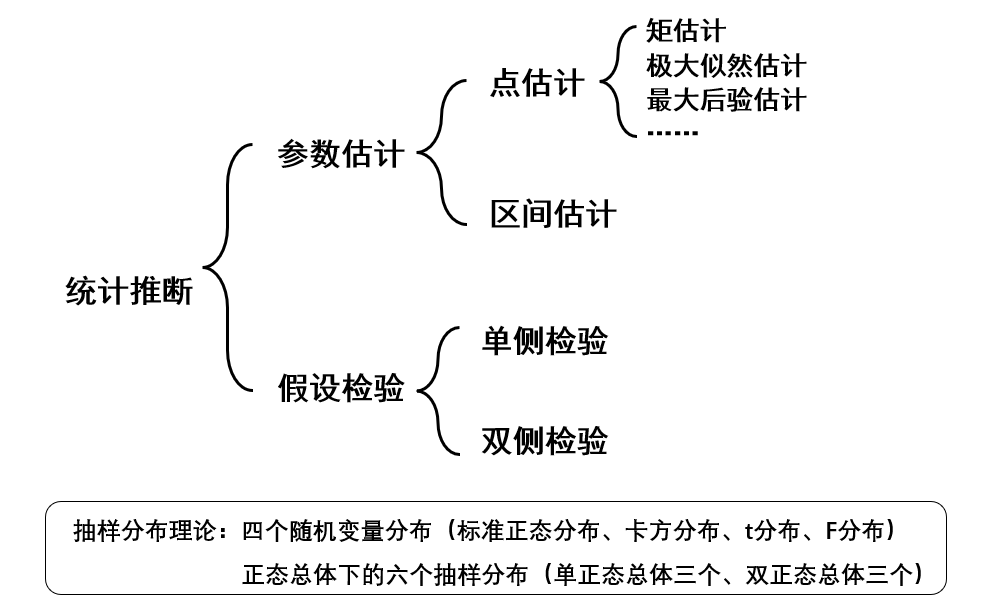
先从整体结构上进行一个把握。数理统计的主要任务是通过样本的信息推断总体的信息,即统计推断工作。统计推断主要有两大类问题:参数估计和假设检验。它们都建立在抽样分布理论的基础之上,但角度不同。参数估计是利用样本信息推断未知的总体参数;而假设检验是先对总体参数提出一个假设值,然后利用样本信息判断这一假设是否成立。参数估计又分为点估计和区间估计,假设检验也可以根据具体问题分为单侧检验和双侧检验。
在正式开始前,对统计量和抽样分布进行简要的介绍,有助于后面的理解。
统计量:统计量是样本的函数,且不含任何未知参数。若 X 1 , X 2 , . . . , X n X_1,X_2,...,X_n X1,X2,...,Xn是总体 X X X 的样本,统计量可表示为 T = T ( X 1 , X 2 , . . . , X n ) T=T(X_1,X_2,...,X_n) T=T(X1,X2,...,Xn)。统计量依赖且只依赖于样本 X 1 , X 2 , . . . , X n X_1,X_2,...,X_n X1,X2,...,Xn,它不含总体分布的任何未知参数。也就是说,当获得了样本观测值后,统计量的值可以被唯一确定下来。
统计量也是随机变量,统计量的分布叫抽样分布 。统计量的分布与样本分布有关,样本分布与未知的总体分布有关,因此抽样分布也与总体分布有关。一般求出统计量的分布是非常困难的事,但如果总体是正态分布,问题会变得相对简单。
以样本平均数为例,它是总体平均数的一个估计量,如果按照相同的样本容量,相同的抽样方式,反复地抽取样本,每次可以计算一个平均数,所有可能样本的平均数所形成的分布,就是样本平均数的抽样分布。
2 参数估计
总体的信息是由总体的分布来刻画的,在实际问题中,往往可以根据问题的背景确定该随机现象的总体所具有的分布类型,但是总体中往往有些参数是未知的。一般来说,这些参数很难精确求出,为此要从总体中抽取样本对其进行估计,这类问题称为参数估计问题。
2.1 点估计
点估计是通过样本值求出总体参数的一个具体的估计量和估计值(这里说的“具体的估计值”是为了和区间估计相对,区间估计是给出区间和置信度,而不是具体的值). 其一般的步骤可概括为 “抽样—构造—代值—计算” :
- 设总体 X X X 的分布函数 F ( x ; θ ) F(x;\theta) F(x;θ) 形式已知,其中含有一个未知参数 θ \theta θ
- 从总体中抽取样本 X 1 , X 2 , . . . , X n X_1,X_2,...,X_n X1,X2,...,Xn
- 构造合适的统计量 g ( X 1 , X 2 , . . . , X n ) g(X_1,X_2,...,X_n) g(X1,X2,...,Xn)作为 θ \theta θ 的估计量,记为 θ ^ = g ( X 1 , X 2 , . . . , X n ) \hat{\theta}=g(X_1,X_2,...,X_n) θ^=g(X1,X2,...,Xn)
- 代入样本观测值 x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn,得到估计值 θ ^ = g ( x 1 , x 2 , . . . , x n ) \hat{\theta}=g(x_1,x_2,...,x_n) θ^=g(x1,x2,...,xn)
2.1.1 矩估计
矩估计法的基本思想是替换原理,即用样本矩替换同阶总体矩。·其依据是由大数定律知,各阶样本矩依概率收敛于同阶总体矩,于是可令各阶样本矩与同阶总体矩相等,下式中 i 代表阶数,k 代表总体中未知参数个数,有几个未知参数就列几个方程: E ( X i ) = A i = 1 n ∑ j = 1 n x j i ( i = 1 , 2 , . . . , k ) E(X^i)=A_i=\frac{1}{n}\sum_{j=1}^nx_j^i\quad(i=1,2,...,k) E(Xi)=Ai=n1j=1∑nxji(i=1,2,...,k)
矩 是对变量分布和形态特点的一组度量。n阶矩被定义为变量的n次方与其概率密度函数之积的积分。直接使用变量计算的矩被称为原始矩(raw moment),移除均值后计算的矩被称为中心矩(central moment)。变量的一阶原始矩等价于数学期望(expectation)、二至四阶中心矩被定义为方差(variance)、偏度(skewness)和峰度(kurtosis)。
举个最简单的例子,设总体 X X X 的分布为 F ( x ; θ ) F(x;\theta) F(x;θ) , θ \theta θ为待估参数, X 1 , X 2 , . . . , X n X_1,X_2,...,X_n X1,X2,...,Xn 为来自总体的样本。那么 E ( X ) E(X) E(X) 应为 θ \theta θ 的函数 h ( θ ) h(\theta) h(θ),由大数定律知样本均值依概率收敛于总体均值,因此可令 E ( X ) = X ‾ = h ( θ ) E(X)=\overline{X}=h(\theta) E(X)=X=h(θ)将样本观测值代入求出 X ‾ \overline{X} X,再解此方程求出 θ \theta θ 即可。这个过程可以看作是用样本一阶矩 X ‾ = 1 n ∑ i = 1 n X i \overline{X}=\frac{1}{n}\sum_{i=1}^nX_i X=n1∑i=1nXi 估计总体一阶矩 E ( X ) E(X) E(X)的过程。结合点估计的一般步骤可知,这里构造的统计量就是样本均值。
【例】 设总体为 X X X ,总体均值 E ( X ) = μ E(X)=\mu E(X)=μ 和总体方差 D ( X ) = σ 2 D(X)=\sigma^2 D(X)=σ2 存在, X 1 , X 2 , . . . , X n X_1,X_2,...,X_n X1,X2,...,Xn 为来自总体的样本,求 μ \mu μ 和 σ 2 \sigma^2 σ2的矩估计量。
要求两个未知参数,令一阶样本矩等于一阶总体矩,二阶样本矩等于二阶总体矩:
{
E
(
X
)
=
X
‾
E
(
X
2
)
=
D
(
X
)
+
[
E
(
X
)
]
2
=
A
2
\begin{cases} E(X)=\overline{X} \\\\E(X^2)=D(X)+[E(X)]^2=A_2 \end{cases}
⎩
⎨
⎧E(X)=XE(X2)=D(X)+[E(X)]2=A2 即:
{
μ
=
X
‾
σ
2
+
μ
2
=
1
n
∑
i
=
1
n
X
i
2
\begin{cases}\mu=\overline{X}\\ \\ \sigma^2+\mu^2=\dfrac{1}{n}\sum\limits_{i=1}^nX_i^2 \end{cases}
⎩
⎨
⎧μ=Xσ2+μ2=n1i=1∑nXi2
解得矩估计量为
{
μ
^
=
X
‾
σ
2
^
=
1
n
∑
i
=
1
n
X
i
2
−
X
‾
2
=
1
n
∑
i
=
1
n
(
X
i
−
X
‾
)
2
\begin{cases}\hat{\mu}=\overline{X}\\ \\ \hat{\sigma^2}=\dfrac{1}{n}\sum\limits_{i=1}^nX_i^2 -\overline{X}^2=\dfrac{1}{n}\sum\limits_{i=1}^n(X_i-\overline{X})^2\end{cases}
⎩
⎨
⎧μ^=Xσ2^=n1i=1∑nXi2−X2=n1i=1∑n(Xi−X)2
- 优点: 直观简单,适用性广,无需知道总体分布的具体形式
- 缺点: 要求总体矩存在,否则不能使用;只利用了矩的信息,没有充分利用分布对参数所提供的信息。
2.1.2 极大似然估计MLE
极大似然估计法(Maximum Likelihood Estimate) 是建立在极大似然原理基础上的。所谓极大似然,可理解为“最大可能性”,即令每个样本属于其真实标记的可能性越大越好。
极大似然原理的直观想法是:概率最大的事最可能出现。设一个随机试验有若干可能结果 A 1 , A 2 , . . . , A n A_1,A_2,...,A_n A1,A2,...,An,若在一次结果中 A k A_k Ak 出现,则认为 A k A_k Ak 出现的概率较大,那未知参数的取值应当满足 A k A_k Ak 发生概率最大。
为了介绍极大似然估计,这里引入似然函数的概念:
似然函数 设 X 1 , X 2 , . . . , X N X_1,X_2,...,X_N X1,X2,...,XN 为来自总体 X X X 的简单随机样本, x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn 为样本观测值,称 L ( θ ) = ∏ i = 1 n p ( x i , θ ) L(\theta)=\prod\limits_{i=1}^np(x_i,\theta) L(θ)=i=1∏np(xi,θ) 为参数 θ \theta θ 的似然函数。
当总体
X
X
X 是离散型随机变量时,
p
(
x
i
,
θ
)
p(x_i,\theta)
p(xi,θ) 表示
X
X
X 的分布列
P
{
X
=
x
i
}
P\{X=x_i\}
P{X=xi} ;
当总体
X
X
X 是连续型随机变量时,
p
(
x
i
,
θ
)
p(x_i,\theta)
p(xi,θ) 表示
X
X
X 的密度函数
f
(
x
,
θ
)
f(x,\theta)
f(x,θ) 在
x
i
x_i
xi处的取值 。
参数 θ \theta θ 的似然函数 L ( θ ) L(\theta) L(θ) 实际上就是样本 X 1 , X 2 , . . . , X N X_1,X_2,...,X_N X1,X2,...,XN 恰好取观测值 x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn (或其邻域)的概率。以离散型为例:
L ( θ ) = P { X 1 = x 1 , X 2 = x 2 , . . . , X n = x n } = P { X 1 = x 1 } P { X 2 = x 2 } . . . P { X n = x n } = ∏ i = 1 n p ( x i , θ ) \begin{aligned} L(\theta) &=P\{X_1=x_1,X_2=x_2,...,X_n=x_n\} \\ &=P\{X_1=x_1\}P\{X_2=x_2\}...P\{X_n=x_n\} \\ &=\prod_{i=1}^np(x_i,\theta)\end{aligned} L(θ)=P{X1=x1,X2=x2,...,Xn=xn}=P{X1=x1}P{X2=x2}...P{Xn=xn}=i=1∏np(xi,θ) 从这个公式也可以看出,极大似然估计的一个重要假设是:来自总体的简单随机样本 X 1 , X 2 , . . . , X N X_1,X_2,...,X_N X1,X2,...,XN 是独立同分布的。
存在一个只与观测值 x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn 有关是实数 θ ^ ( x 1 , x 2 , . . . , x n ) \hat{\theta}(x_1,x_2,...,x_n) θ^(x1,x2,...,xn) ,使 L ( θ ^ ) = m a x L ( θ ) L(\hat{\theta})=max\ L(\theta) L(θ^)=max L(θ) ,则称 θ ^ ( x 1 , x 2 , . . . , x n ) \hat{\theta}(x_1,x_2,...,x_n) θ^(x1,x2,...,xn) 为参数 θ \theta θ 的最大似然估计值, θ ^ ( X 1 , X 2 , . . . , X n ) \hat{\theta}(X_1,X_2,...,X_n) θ^(X1,X2,...,Xn)是极大似然估计量。
极大似然估计对未知参数的数量没有要求,可以求一个,也可以一次求出多个。它要求总体的分布是已知的。由于似然函数是多个函数乘积的形式,为简化运算可以考虑对 L ( θ ) L(\theta) L(θ) 取对数得到对数似然函数 I n L ( θ ) InL(\theta) InL(θ)
【例】 设总体 X ∼ N ( μ , σ 2 ) X\sim N(\mu,\sigma^2) X∼N(μ,σ2) , X 1 , X 2 , . . . , X n X_1,X_2,...,X_n X1,X2,...,Xn 为来自总体的样本,求未知参数 μ \mu μ 和 σ 2 \sigma^2 σ2的最大似然估计量。
2.1.3 最大后验估计MAP
2.1.4 最小二乘估计
2.1.5 贝叶斯估计
2.2 区间估计
3 假设检验
【几年前的草稿,发出来先用着、、、】