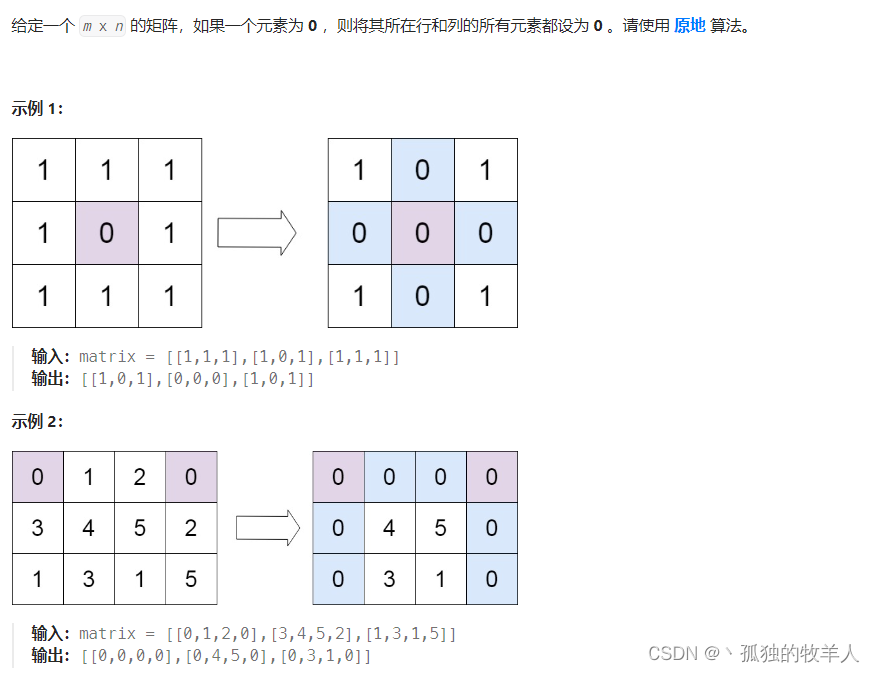
思路一：
用一个同样大小的矩阵记录0的位置，然后遍历矩阵置0，
空间复杂度为O（mn）

class Solution {
    public void setZeroes(int[][] matrix) {
        int [][] matrix_new = new int[matrix.length][matrix[0].length];
          for(int i=0 ; i < matrix.length;i++)
        {
            for(int j = 0 ; j < matrix[0].length ; j++)
            {
                    matrix_new[i][j] = 1;
            }
        }
        for(int i = 0; i < matrix.length;i++)
        {
            for(int j = 0 ; j < matrix[0].length ; j++)
            {
                if(matrix[i][j] == 0)
                {
                    for(int k=0 ; k < matrix[0].length ; k++)
                    {
                        matrix_new[i][k] = 0;
                    }
                    for(int k=0 ; k < matrix.length ; k++)
                    {
                        matrix_new[k][j] = 0;
                    }
                }
            }
        }
        for(int i = 0 ; i < matrix.length;i++)
        {
            for(int j = 0 ; j < matrix[0].length ; j++)
            {
                if(matrix_new[i][j] != 0)
                {
                    matrix_new[i][j] = matrix[i][j];
                }
            }
        }
        for(int i = 0 ; i < matrix.length;i++)
        {
            for(int j = 0 ; j < matrix[0].length ; j++)
            {
                    matrix[i][j] = matrix_new[i][j];
            }
        }
    }
}

表现一般般

咱们优化一下，思路2：
通过观察我们发现，只要一个元素为0，那么它所在的行和列都为0。我们只需记录下来所有0元素的行和列，就能将矩阵置0。
那么空间复杂度为O（m+n）

class Solution {
    public void setZeroes(int[][] matrix) {
        int m = matrix.length , n = matrix[0].length;
        Set<Integer> rows = new HashSet<Integer>();//最大为m
        Set<Integer> columns = new HashSet<Integer>();//最大为n
        for(int i = 0 ; i < m ; i++)
        {
            for(int j = 0 ;j < n ; j++)
            {
                if(matrix[i][j] == 0)
                {
                    rows.add(i);
                    columns.add(j);
                }
            }
        }
        for(Integer i : rows)
        {
            for(int j = 0 ; j < n ; j++)
            {
                matrix[i][j] = 0;
            }
        }
        for(Integer i : columns)
        {
            for(int j = 0 ; j < m ; j++)
            {
                matrix[j][i] = 0;
            }
        }
    }
}

相对比与思路一，有所进步

思路三：再思考观察，我们发现，除去第一行和第一列，若元素matrix[i][j]为0，那么matrix[i][0]与matrix[0][j]也必0。我们就可以利用第一行第一列记录需要置0的行和列。原地置零，空间复杂度O（1）。

class Solution {
    public void setZeroes(int[][] matrix) {
        int row = matrix.length;
        int col = matrix[0].length;
        boolean row0_flag = false;
        boolean col0_flag = false;
        // 第一行是否有零
        for (int j = 0; j < col; j++) {
            if (matrix[0][j] == 0) {
                row0_flag = true;
                break;
            }
        }
        // 第一列是否有零
        for (int i = 0; i < row; i++) {
            if (matrix[i][0] == 0) {
                col0_flag = true;
                break;
            }
        }
        // 把第一行第一列作为标志位
        for (int i = 1; i < row; i++) {
            for (int j = 1; j < col; j++) {
                if (matrix[i][j] == 0) {
                    matrix[i][0] = matrix[0][j] = 0;
                }
            }
        }
        // 置0
        for (int i = 1; i < row; i++) {
            for (int j = 1; j < col; j++) {
                if (matrix[i][0] == 0 || matrix[0][j] == 0) {
                    matrix[i][j] = 0;
                }
            }
        }
        if (row0_flag) {
            for (int j = 0; j < col; j++) {
                matrix[0][j] = 0;
            }
        }
        if (col0_flag) {
            for (int i = 0; i < row; i++) {
                matrix[i][0] = 0;
            }
        } 
    }
}

不知道为什么表现没有思路2的好。