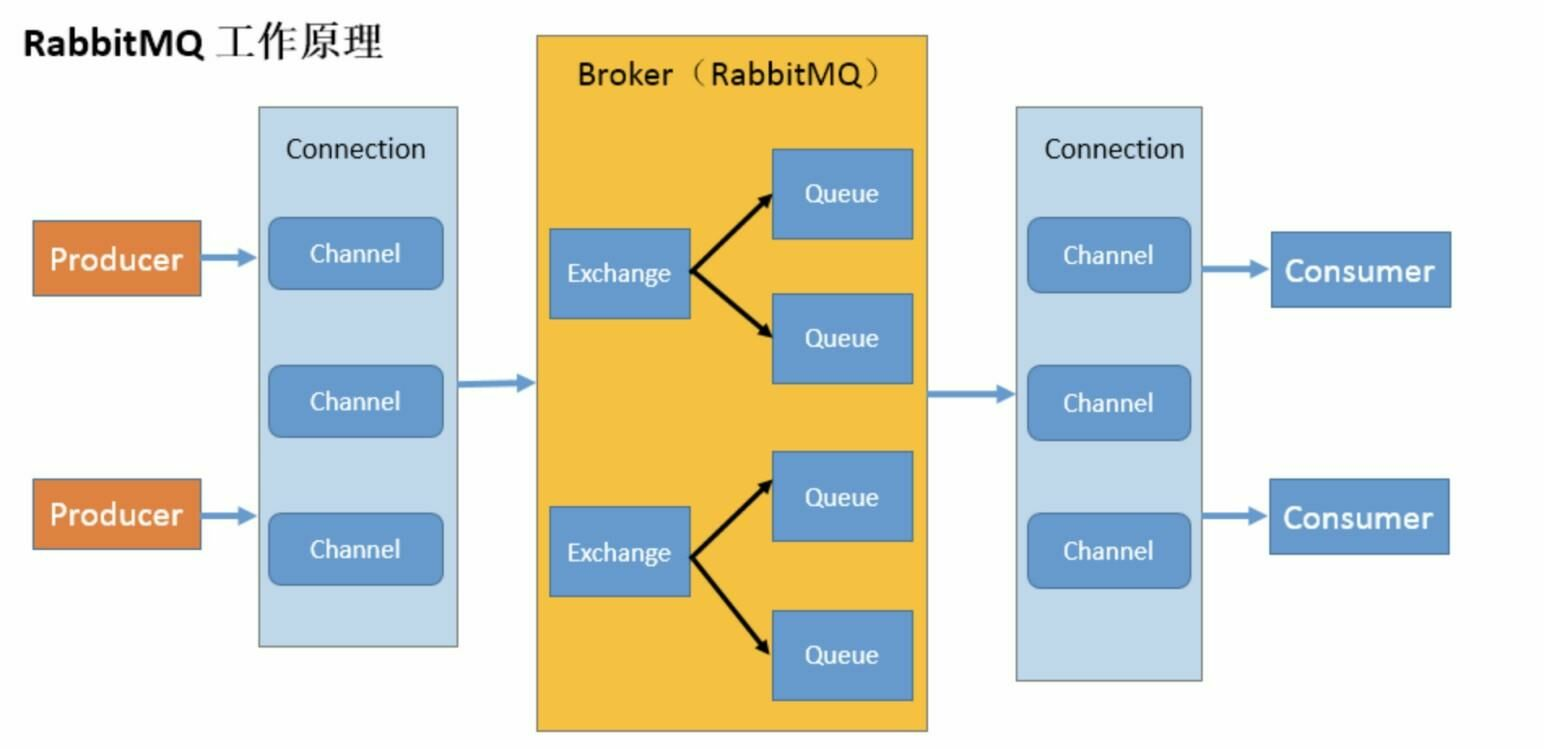
提示:分析scipy.signal.hilbert和scipy.fftpack.hilbert在应用的区别
一、代码
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
from pyhht import EMD
from scipy.signal import hilbert
import tftb.processing
from scipy import signal, fftpack, stats
matplotlib.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文
matplotlib.rcParams['axes.unicode_minus'] = False # 显示负号
def envelope_spectrum1(data1, fs):
'''
fun: 绘制包络谱图
param data: 输入数据,1维array
param fs: 采样频率
param xlim: 图片横坐标xlim,default = None
param vline: 图片垂直线,default = None
'''
plt.figure(figsize=(15, 8))
plt.plot(data1)
# ----去直流分量----#
data = np.array(data1)
data = data - np.mean(data)
# ----做希尔伯特变换----#
xt = data
ht = fftpack.hilbert(xt)
at = np.sqrt(xt ** 2 + ht ** 2) # 获得解析信号at = sqrt(xt^2 + ht^2)
plt.plot(at)
plt.show()
# 计算各组分的Hilbert变换
imfsHT = hilbert(xt)
# 计算各组分Hilbert变换后的瞬时频率
instf, timestamps = tftb.processing.inst_freq(imfsHT)
plt.figure(figsize=(15, 8))
plt.plot(instf*fs)
plt.show()
am = np.fft.fft(at) # 对解析信号at做fft变换获得幅值
am = np.abs(am) # 对幅值求绝对值(此时的绝对值很大)
am = am / len(am) * 2
am = am[0: int(len(am) / 2)] # 取正频率幅值
freq = np.fft.fftfreq(len(at), d=1 / fs) # 获取fft频率,此时包括正频率和负频率
freq = freq[0:int(len(freq) / 2)] # 获取正频率
am[0] = 0
plt.figure(figsize=(15, 8))
plt.plot(am)
plt.show()
return freq, am
if __name__ == "__main__":
# 生成0-1时间序列,共2048个点
N = 1000
t = np.linspace(0, 1, N)
# 生成信号
# signal = (2 + np.cos(8 * np.pi * t)) * np.cos(40 * np.pi * (t + 1) ** 2) + np.cos(
# 20 * np.pi * t + 5 * np.sin(200 * np.pi * t))
signal = 0.8 *np.cos(90 * np.pi * t * 2) + np.sin(100 * np.pi * t * 2)
freq, am = envelope_spectrum1(signal, N)
二、调试代码
- at: 是scipy.fftpack.hilbert(xt)的结果
- imfsHT: 是scipy.fftpack.hilbert(xt)的结果(在代码里是hilbert(xt)的结果)
- data(ht):是原始信号
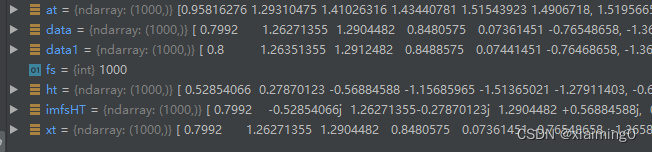
可以发现at和imfsHT的虚部相差一个负号。
可以发现data和imfsHT的实部。
三、实际应用
yt = xt + ht*j
- yt:是解调信号
- xt:是解调信号的实部
- ht:是解调信号的虚部
at = np.sqrt(xt ** 2 + ht ** 2) # 解调信号的瞬时幅值用于包络解调
也可以通过xt和ht计算瞬时频率——信号的时频分析(HHT:希尔伯特黄变换)