Logistic Regression——逻辑回归

news2024/10/5 15:28:20

1. 为什么需要逻辑回归

在前面学习的线性回归中，我们的预测值都是任意的连续值，例如预测房价。除此之外，还有一个常见的问题就是分类问题，而逻辑回归是一个解决分类问题的模型，其预测值是离散的。

分类问题又包括二分类问题与多分类问题，对于二分类问题来说，预测值只可能是\否即1\0,

对于多分类问题来说，预测值可能是多个分类中的一个，例如我输入的是一些动物的图片，我想让模型辨认这些是什么动物，我可以设定预测值1代表模型认为输入是一只猫，预测值2代表模型认为输入是一只狗，预测值3代表模型认为输入是一只猪。

2. 二分类逻辑回归

2.1 从线性回归到分类

如果有这样一个场景，输入x为肿瘤的大小，而需要预测是否是恶性的。接下来我们仍然使用线性回归模型，但如果我们这增设这样一个阈值

这样一来，所有预测值都将变成1或者0，实现了分类的目的

2.2 逻辑回归模型

对于线性回归的模型来说，其输出值是任意的，常常会远远大于1或者远远小于0，仅仅上述的阈值可能并不会起到作用或者效果很差。

对此，逻辑回归会先将所有预测值通过sigmoid 函数映射到[0,1]区间，函数表达式和图像如下图

（z为输入）

sigmoid 函数是一个非线性函数，当x大于0时，输出值大于0.5，当x<0时输出值小于0.5

最终我们得到逻辑回归的模型如下

$h_{\theta }(x)$ 作用是，对于给定的输入变量，通过参数 $\theta$ 计算输出变量为1的可能性是多少

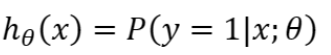
假如对于一个输入x，最终计算出 $h_{\theta }(x)$ =0.7，则模型认为有70%的可能其为正向类（=1），相反负向类的可能性就为1-0.7=0.3

最后在分类时，再入加上之前的阈值

所以逻辑回归就是线性回归再嵌套一个非线性的sigmoid函数，其本质还是回归

2.4 决策边界（Decision Boundary）

假如分类这样一些数据，‘x’为1，圈为0

通过建立逻辑回归模型

假设经过训练我们得到了这样一组参数，于是得到嵌套在逻辑回归里的线性回归模型 $\theta^{\top }X=-3+x_{1}+x_{2}$ ，根据逻辑回归的原理当 $-3+x_{1}+x_{2}>=0$ 时预测1，当 $-3+x_{1}+x_{2}<0$ 时预测0，于是分隔情况就是 $-3+x_{1}+x_{2}=0$ ，我们可以画出这个直线

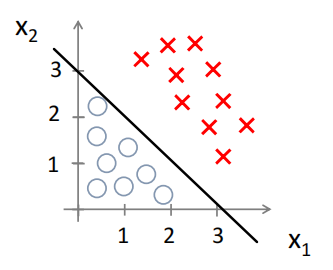
这条线便是模型的决策边界

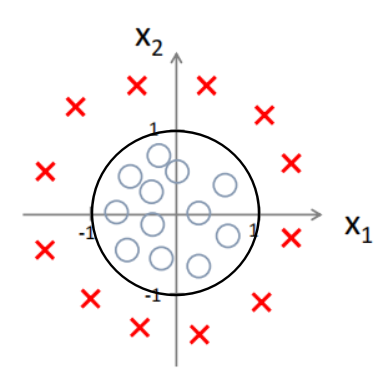
如果是这样的数据

建立逻辑回归模型、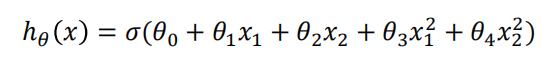

得到参数

同样的原理，得到其决策边界，是一个圆心在原点，半径为1的圆

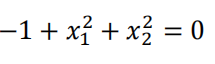
2.5 损失函数

2.5.1 为什么不用MSE损失函数

根据上述的理论可以知道，逻辑回归的和线性回归的本质是一样的。那是不是意味着损失函数也可以用MSE。

在线性回归中损失函数如下

$J(\theta )=\frac{1}{2m}\sum_{i=1}^{m}(h_{\theta }^{i}-y^{i})^{2}$

我们将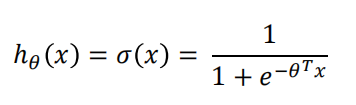带入可以得到

$J(\theta )=\frac{1}{2m}\sum_{i=1}^{m}(\frac{1}{1+e^{\theta ^{\top }x}}-y)^{2}$

得到的是一个非凸函数（non-convexfunction），这会很大程度上影响梯度下降法寻找全局最小值，很可能停留在在某个局部极小值

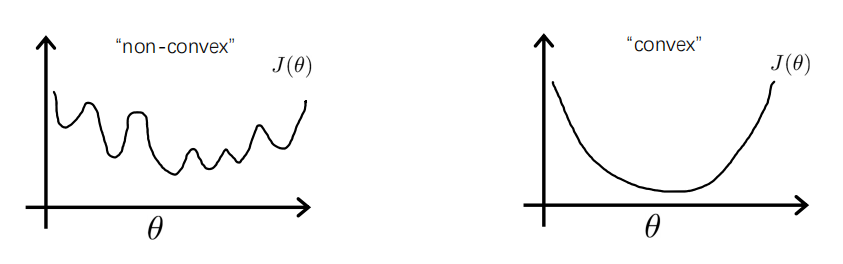
2.5.2 对数损失函数

介于上述问题，对于二分类逻辑回归来说，使用的是对数损失函数。

对于一个样本来说，预测值会有1和0两种情况，对应两个损失值

（log一般以e为底）

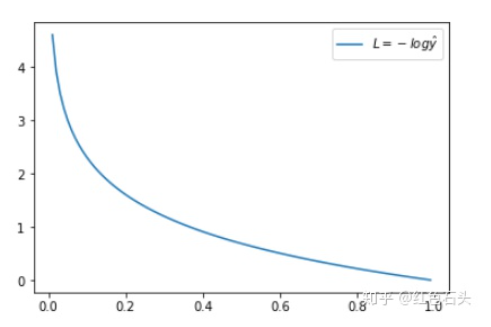
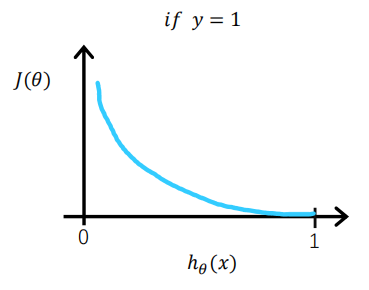
当实际y=1时，如果预测值 $h_{\theta }(x)$ =1，此时预测是完全正确的，代入上式计算误差为0，如果预测值 $h_{\theta }(x)$ 不为1，代表模型没有100%的把握认为这是正向类的，此时误差会随着 $h_{\theta }(x)$ 的减小而变大。

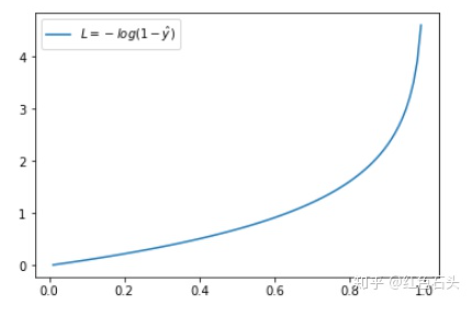
当实际y=0时，如果预测值 $h_{\theta }(x)$ =0，此时预测是完全正确的，代入上式计算误差为0，如果预测值 $h_{\theta }(x)$ 不为0，代表模型没有100%的把握认为这是负向类的，此时误差会随着 $h_{\theta }(x)$ 的增大而变大。

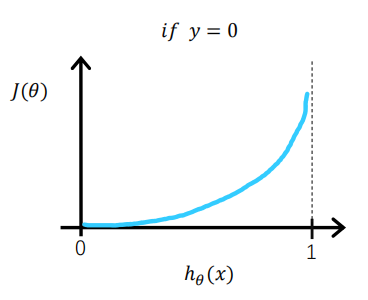
将这两种情况合在一起

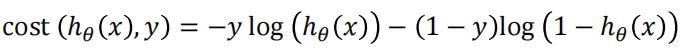
再求和取平均得到最终损失函数表达式

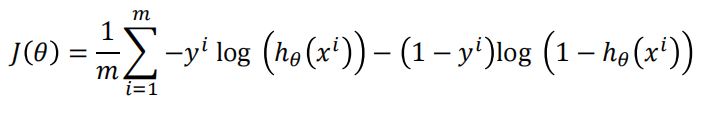
采用矩阵的形式表达

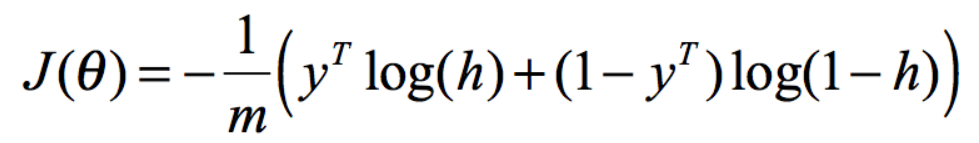
2.6 梯度下降

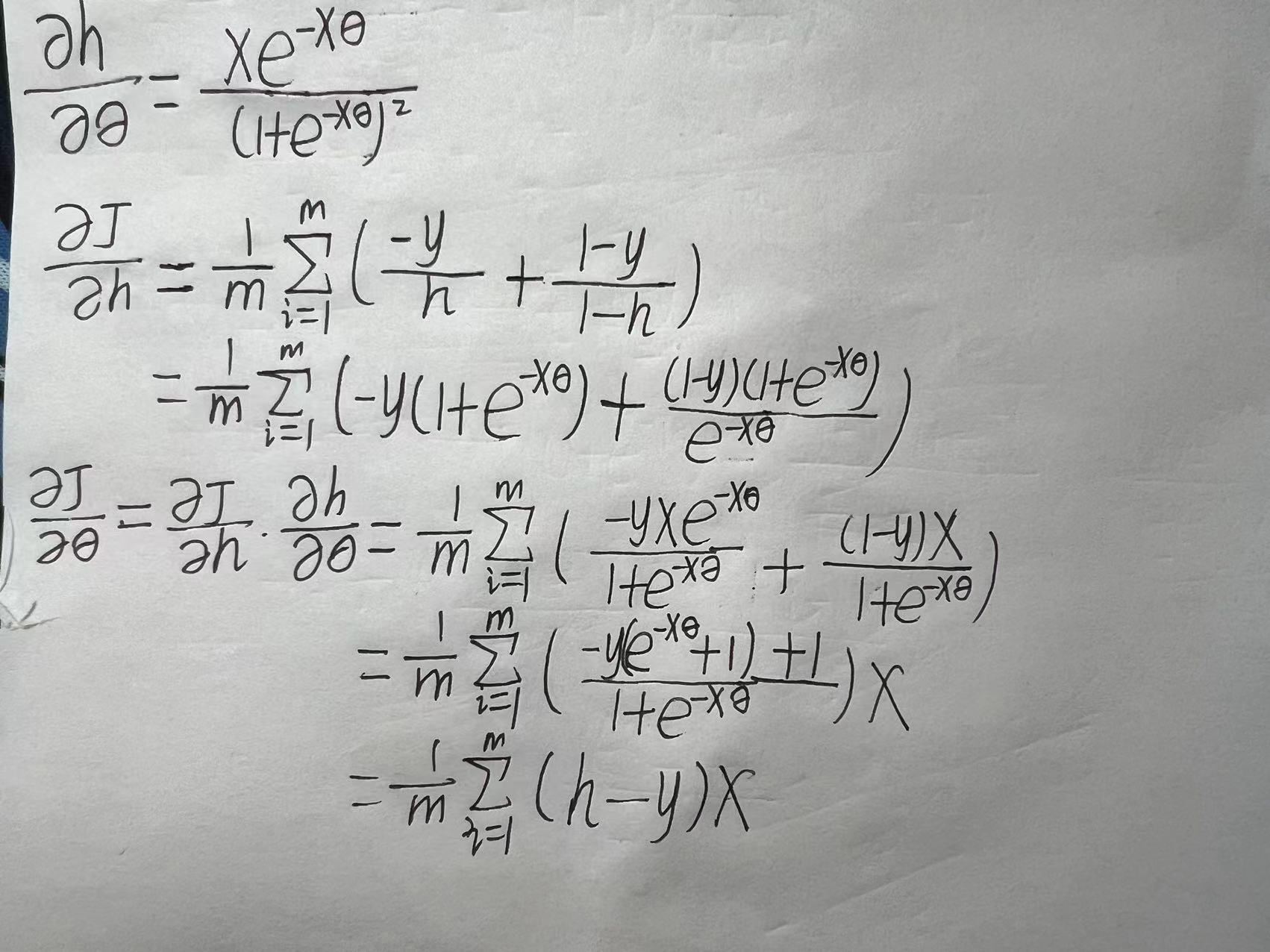
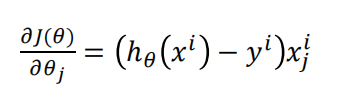
矩阵表达式为

使用梯度下降

矩阵表达式为

$\theta = \theta -\frac{\alpha }{m}X^{\top }(h-y)$

3. 多分类逻辑回归

多分类逻辑回归的实现依赖于二分类

将其中一个类标记为正向类，然后将其他类都标记为负向类，得到一个模型 $h_{\theta }^{1}(x)$ ，接着选择另外一个类标记为正向类，然后将其他类都标记为负向类，又得到一个模型 $h_{\theta }^{2}(x)$ ，以此类推，我们可以得到一系列模型，假设有k个类

$h_{\theta }^{i}(x)=p(y=i|x;\theta )$ ,i=（1，2，3，4……k）

训练好这一系列模型后，对于一个输入x，让其在所有的分类器都得到一个输出，最后选择一个max $h_{\theta }(x)$ 作为最终的输出

4. 逻辑回归的实例

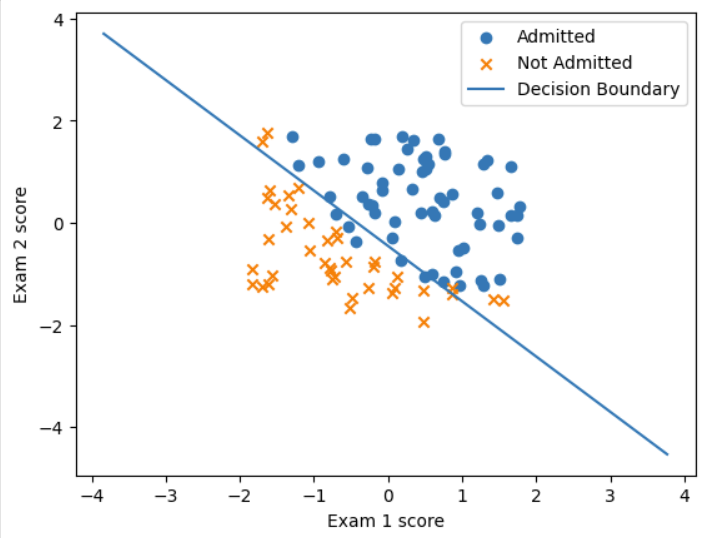
ex2data1数据集包含100行数据前两列是学生的两种考试的成绩，最后一列是他们被是否录取。需要根据学生的两种考试的成绩来预测他们被是否录取。

1.读取数据集

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

data = pd.read_csv('ex2data1.txt',names=['exam1','exam2','admitted'])
data.head()

# 根据admitted的值分类
plt.scatter(positive['exam1'],positive['exam2'],marker='o',label='Admitted')
plt.scatter(negative['exam1'],negative['exam2'],marker='x',label='Not Admitted')
plt.xlabel('Exam1 Score')
plt.ylabel('Exam2 Score')
plt.legend()
plt.show()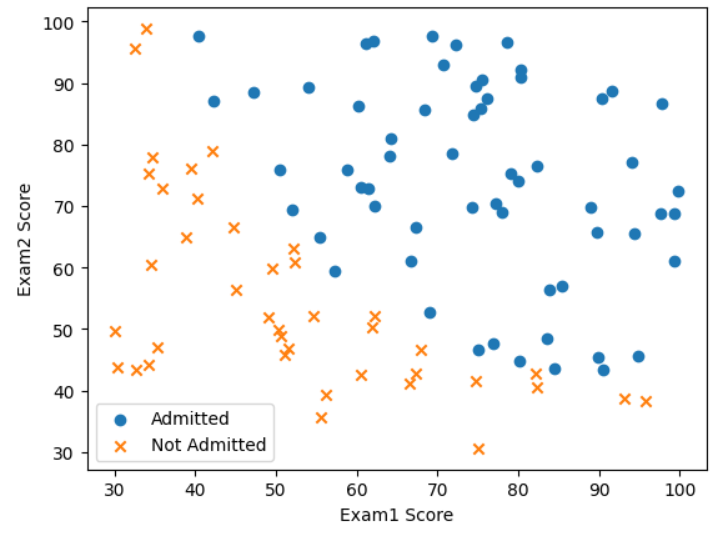

2.数据预处理

data.insert(0,'ones',1)
X = data.iloc[:,0:-1].values
y = data.iloc[:,-1].values
y = y.reshape(100,1)

3.定义Sigmoid函数

def sigmoid(z):
    return 1/(1+np.exp(-z))

4.定义损失函数

def lossFunction(X,y,theta):
    m = len(X)
    h = sigmoid(X@theta)
    return (1/m)*np.sum(-y.T@np.log(h)-(1-y).T@np.log(1-h))

5.模型训练

def train(X,y,alpha,epochs):
    loss_history = []
    theta = np.random.rand(3,1)
    for i in range(epochs):
        m = len(X)
        h = sigmoid(X@theta)
        theta = theta - (alpha/m)*X.T@(h-y)
        current_loss = lossFunction(X,y,theta)
        loss_history.append(current_loss) 
        if (i+1) % 100 == 0:
            print("epochs={},current_loss={}".format(i+1,current_loss))
     # 绘制损失函数图像
    plt.plot(range(1,epochs+1),loss_history)
    plt.xlabel('epochs')
    plt.ylabel('loss')
    plt.title('Loss Curve')
    plt.show()
    return theta

# 参数
alpha = 0.1
epochs = 1000
theta = train(X,y,alpha,epochs)

admitted = X[y.flatten() == 1]
not_admitted = X[y.flatten() == 0]
plt.scatter(admitted[:, 1], admitted[:, 2], label='Admitted', marker='o')
plt.scatter(not_admitted[:, 1], not_admitted[:, 2], label='Not Admitted', marker='x')
plt.xlabel('Exam 1 score')
plt.ylabel('Exam 2 score')

# 绘制决策边界
plot_x = np.array([min(X[:, 1]) - 2, max(X[:, 1]) + 2])
plot_y = (-1 / theta[2]) * (theta[1] * plot_x + theta[0])
plt.plot(plot_x, plot_y, label='Decision Boundary')
plt.legend()
plt.show()