Problem: 90. 子集 II

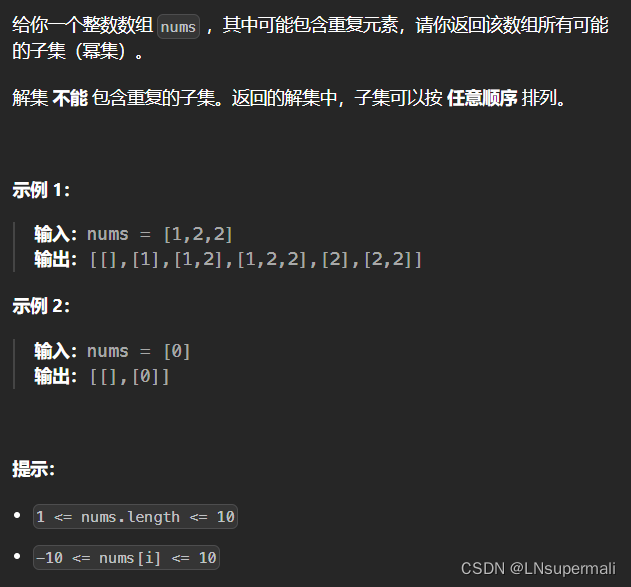
题目描述

思路

在本题中所给数组nums中的元素有重复，若再直接使用回溯的话会使得最终的子集有重复；其次我们应该知道求子集，求组合这类使用回溯处理的题目，在核心处理回溯时，都是以当前决策阶段为起始位置开始循环遍历（也可以理解为开始当前决策阶段的穷举），并且以当前决策阶段为基础开始下一阶段（递归调用），则在本题中：

1.对给定数组nums排序
2.在回溯函数中我们每次是令当前层的循环起始位置（i）等于当前的决策阶段（start），然后每次我们判断若i > start && nums[i] == nums[i-1]则表示这个分支（因为回溯实则上是在对决策树进行遍历处理）是重复的，则我们不“遍历”该分支（即不进行递归调用），以达到减枝删去重复元素的作用

解题方法

1.定义二维集合result作为结果集合存储每个子集，一维集合path作为决策路径
2.对原来给定的数组nums排序，并从0阶段开始调用回溯函数
3.回溯函数中:

3.1每次开始将当前决策阶段中的决策路径添加到结果集result中(即添加当前得到的子集)；
3.2for循环开始当前决策阶段的穷举，循环起始位置是当前的决策阶段（假定为start），并判断若i > start && nums[i] == nums[i-1]则continue，以达到减枝去重的效果，否则在当前决策阶段的基础上递归下一阶段，最后恢复当前决策阶段的决策路径状态

复杂度

时间复杂度:

$O(n\times 2^n)$

空间复杂度:

$O(n)$

Code

class Solution {
    //Result list
    private List<List<Integer>> result = new ArrayList<>();
    //Decision path
    private List<Integer> path = new ArrayList<>();

    /**
     * Gets all subsets of a collection containing duplicate elements
     *
     * @param nums A collection of repeating elements
     * @return List<List < Integer>>
     */
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        Arrays.sort(nums);
        backtrack(nums, 0);
        return result;
    }

    /**
     * Use backtracking to get all subsets of a collection containing duplicate elements
     *
     * @param nums  A collection of repeating elements
     * @param start Decision stage
     */
    public void backtrack(int[] nums, int start) {
        //Add the subset of current decision path to the result
        result.add(new ArrayList<Integer>(path));

        //Iterate from start, removing elements that have already been selected
        for (int i = start; i < nums.length; ++i) {
            //Cutting branch(remove the repetitive subset)
            if (i > start && nums[i] == nums[i - 1]) {
                continue;
            }
            //Adds the current optional element to the decision path
            path.add(nums[i]);
            backtrack(nums, i + 1);
            //Recover the current decision path
            path.remove(path.size() - 1);
        }
    }
}