文章目录
- 第一节:补码讲解及内存实战演练
- 1. 补码讲解
- 2. 反码
- 第二节:整型不同类型解析-溢出解析
- 1. 整型不同类型解析
- 2. 溢出解析
- 第三节:IEEE754标准解析
- 第四节:浮点型精度丢失
第一节:补码讲解及内存实战演练
1. 补码讲解
计算机的CPU无法做减法操作,只能做加法操作。CPU中有一个逻辑单元叫加法器。
计算机所做的减法,都是通过加法器将其变化成加法实现的。
小端存储:X86架构都是使用的小端存储。小端存储是低字节在前,即低字节在低地址。高字节在后,即高字节在高地址,fb对于0xffffffffb是低字节,因此fb在内存中最前面。大端和小端相反。

负数在内存中以补码的形式存储。
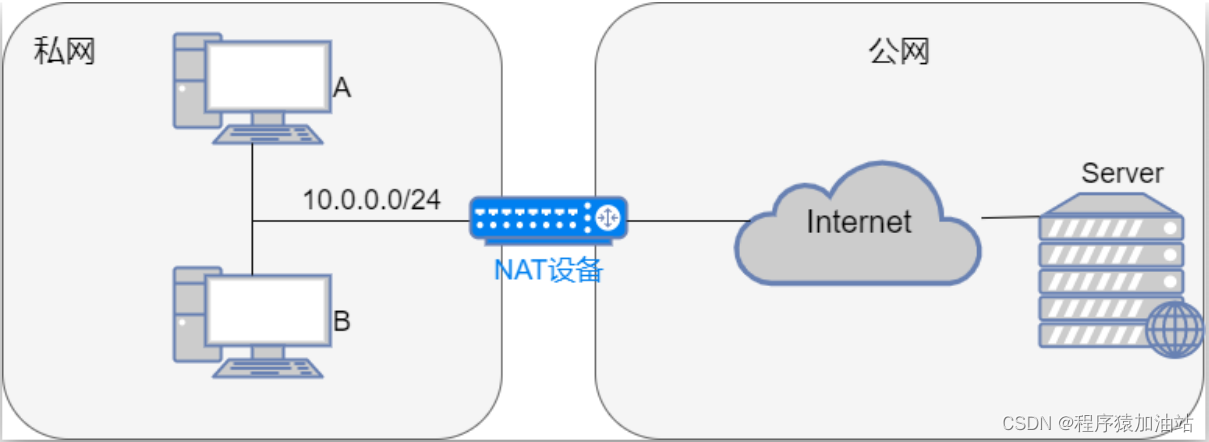
问题:如何实现2-5?
实现2-5的方法是2+(-5),由于计算机只能存储0和1,5的二进制数为101,称为原码。计算机用补码表示-5,补码是对原码取反后加1的结果。

如上图:-5在内存中存储为0xfffffffb,对其加2后得0xfffffffd它就是k的值。当最高位为1时表示负数。我们在通过取反加1得到原码,也就是3,由于是负数,所以就是-3。

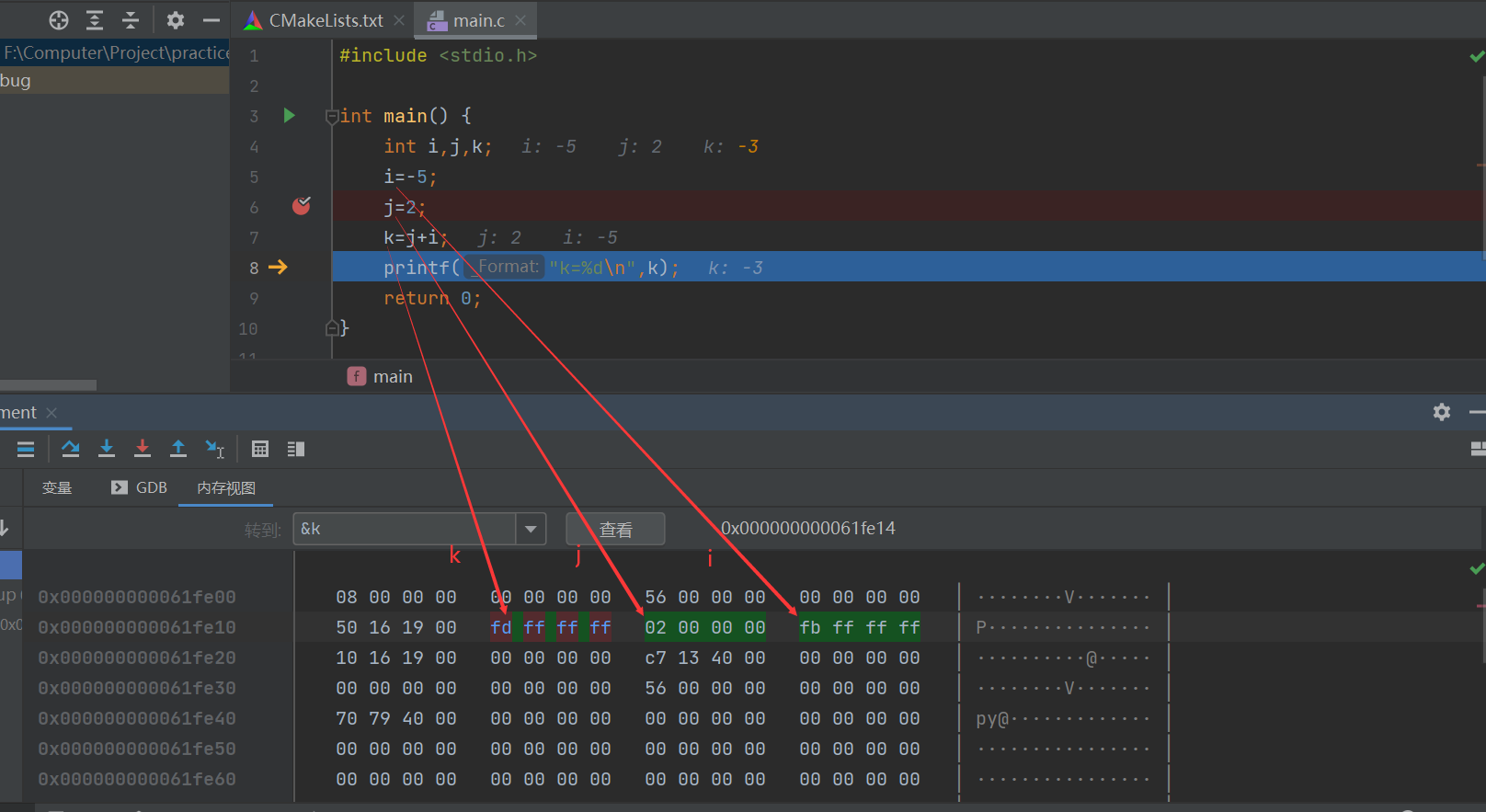
说明:补码得原码的时候先取反再加1和先减1再取反效果一样。
注意:通过8位表示,-5的补码为1111 1011,-5的原码为10000 0101,符号位不动的,只有值的部分是5。
2. 反码
反码是一种在计算机中数的机器码表示。对于单个数值(二进制的0和1)而言,对其进行取反操作就是将0变成1,1变成0,正数的反码和原码一样,负数的反码就是在原码的基础上符号位保持不变,其他位取反。
第二节:整型不同类型解析-溢出解析
1. 整型不同类型解析
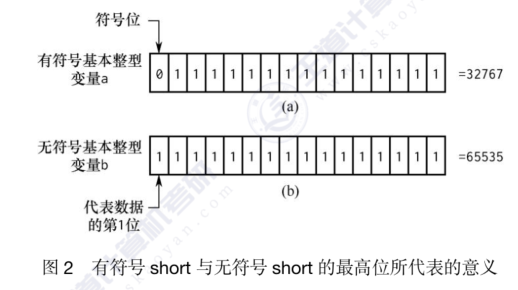
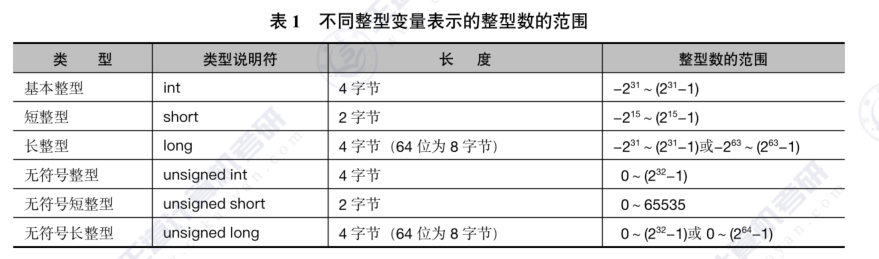
整型变量包括6中类型。有符号与无符号整型的最高位代表的意义不同。

不同整型变量表示的整型范围如表所示,超出范围会发生溢出现象,导致计算出错。
2. 溢出解析
有符号短整型可以表示的最大值为32767,当我们对其加1时,b的值会变成多少呢?实际运行打印得到的是-32768,为什么会这样呢?因为32767对应的十六进制数为0x7fff,加1后变为0x8000,其首位为1,因此变成了一个负数,去这个负数的原码后,就是其本身,值为32768,所以0x8000是最小的负数,即-32768,因此导致计算结果出错。
#include <stdio.h>
int main() {
int i=10;
short a=32767;
short b=0;
long c;
b=a+1; // 发生了溢出,解决溢出的办法是用更大的空间来存
printf("b=%d\n",b); // b并不是32767
printf("---------------\n");
unsigned int m=3;
unsigned short n=0x8056; // 无符号类型,最高位不认为是符号位
unsigned long k=5;
b=0x8056;
printf("b=%d\n",b); // b是有符号类型,所以输出是负值
printf("n=%u\n",n); // 无符号类型要用%u,用%d是不规范的
return 0;
}
F:\Computer\Project\practice\20\20.4-overflow\cmake-build-debug\20_4_overflow.exe
b=-32768
---------------
b=-32682
n=32854
进程已结束,退出代码为 0
第三节:IEEE754标准解析
float型变量占用的内存空间为4字节,double型变量占用的内存空间为8字节。
与整型数据的存储方式不同,浮点型数据是按照指数形式存储的。系统把一个浮点型数据分成小数部分(用M表示)和指数部分(用E表示)并分别存放,指数部分采用规范化的指数形式,指数也分为正、负(符号位,用S表示)。

数符(即符号位)占1位,是0时代表正数,是1时代表负数。
4.5的IEEE-754浮点型变量存储标准
| 格式 | SEEEEEEE | EMMMMMMM | MMMMMMMM | MMMMMMMM |
|---|---|---|---|---|
| 二进制 | 0100 0000 | 1001 0000 | 0000 0000 | 0000 0000 |
| 十六进制 | 40 | 90 | 00 | 00 |
S:S是符号位,用来表示正、负,是1表示负数,是0表示正数。
E:E代表指数部分(指数部分的值规定只能是1到254,不能全是0或全是1),指数部分运算前都要减去127,因为还要表示负指数。这里的10000001转换为十进制数为129,129-127=2,即实际指数部分为2.
M:M代表小数部分,这里为0010 0000 0000 0000 0000 000,底数左边省略存储了一个1,使用的实际底数表示为1.00100000000000000000000。
上面表1可以变为如下表格:
| S(符号位) | E(阶码) | M(尾数) |
|---|---|---|
| 0 | 1000 0001 | 0010 0000 0000 0000 0000 000 |

可以看到,4.5的内存是0x40900000。

首先看f的小数部分,也就是表中M(灰色)的部分。这里为0010 0000 0000 0000 0000 000.总计23位。由于底数左边省略存储了一个1,所以实际底数部分表示为1.00100000000000000000000。
在看指数部分,计算机并不能直接计算10的幂次,f的指数部分为1000 0001,其十进制值为129,129-127=2,即实际指数部分为2,指数值为2,代表2的2次幂。因此将1.001左移2位即可,也就是100.1,然后转换成十进制数,整数部分为4,小数部分为2的-1次方,为0.5,因此十进制数为4.5。
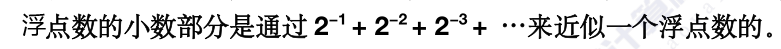

1.456的内存为0x355eba3f。
首先看f1的小数部分,是表中Mhuise代表的部分,这里为011 1010 0101 1110 0011 0101,总计23位。底数左边省略存储了一个1,实际底数表示为1.011 1010 0101 1110 0011 0101。
指数部分:计算机不能直接计算10的幂次,f1的指数部分为0111 1111,其十进制为127,127-127=0,即实际指数部分为0指数,代表2的0次幂,为1。因为1.011 1010 0101 1110 0011 0101无需做移动。
1+0.25+0.125+0.0625+0.015625=1.453125。
第四节:浮点型精度丢失
浮点型变量分为单精度(float)型,双精度(double)型。
浮点型使用的是指数表示法,需要记忆数值范围。
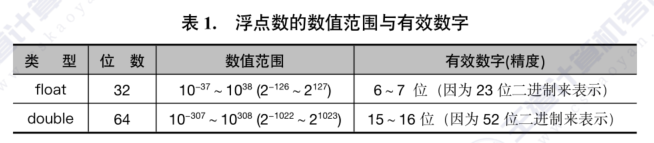
表中的double类型是-1022到1023,是通过1-2046(不能全是0或全是1,全1是2047)减去1023,得到-1022到1023。
#include <stdio.h>
// 提醒:scanf读取double类型是,要用lf,如double d;scanf("%lf",&d);
int main() {
float a=1.23456789e10;
float b;
b=a+20; // 计算时精度丢失
printf("b=%f\n",b); // %f既可以输出float,也可以输出double类型
return 0;
}
F:\Computer\Project\practice\20\20.6-double\cmake-build-debug\20_6_double.exe
b=12345678848.000000
进程已结束,退出代码为 0
分析:对于程序中,我们赋给a的值为1.23456789e10,加20后,应该得到的值是1.234567892e10,但b输出的结果却是b=12345678848.000000,变得更小了。我们将这种现象称为精度丢失,因为float类型数据能够表示的有效数字为7位,最多只保证1.234567e10的正确性。要使结果正确,就需要把a和b均改为double类型,因为double可以表示的精度为15-16位。
注意:对于强制类型转换,int转float可能造成精度丢失,因为int是有10位有效数字的,但是int强制转为double不会,float转为double也不会丢失精度。