图论(Graph Theory)是数学的一个分支。它以图为研究对象。图论中的图是由若干给定的点及连接两点的线所构成的图形,这种图形通常用来描述某些实体之间的某种特定关系,用点代表实体,用连接两点的线表示两个实体间具有的某种关系。
相比矩阵、张量、序列等结构,图结构可以有效建模和解决社会关系、交通网络、文法结构和论文引用等需要考虑实体间关系的各种实际问题。因此,为了能够有效利用图结构这种工具,我们必须要对图的定义、类型和性质有一定的认识。
概念
图是由顶点(vertex)和边(edge)组成的数据结构
如下图:
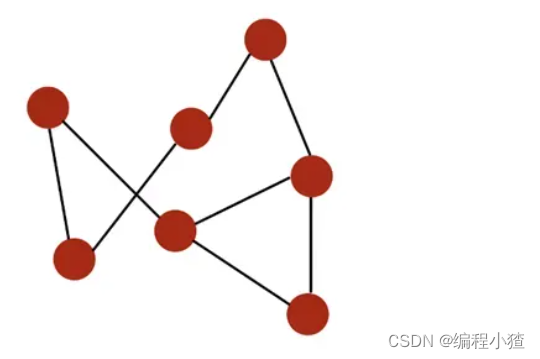
节点(node)用红色标出,通过黑色的边(edge)连接。
图可用于表示:
- 社交网络
- 网页
- 生物网络
- …
我们可以在图上执行怎样的分析?
- 研究拓扑结构和连接性
- 群体检测
- 识别中心节点
- 预测缺失的节点
- 预测缺失的边
- …
为了方便大家的学习,下面我先来介绍一下图的基本术语。
基本术语
图的分类
有向图(Directed Graph):
- 在有向图中,每条边都有一个方向,从一个顶点指向另一个顶点。
- 如果顶点 A 到顶点 B 有一条有向边,则我们称顶点 A 直接指向顶点 B。这意味着从顶点 A 出发可以到达顶点 B,但反之则不一定成立。
- 有向图常用于表示具有方向性关系的问题,例如交通流向、网页链接、任务依赖关系等。
无向图(Undirected Graph):
- 在无向图中,边没有方向,即连接两个顶点的边可以被看作是双向的。
- 如果顶点 A 与顶点 B 之间有一条边,那么顶点 A 与顶点 B 之间是相互连通的,可以双向移动。
- 无向图常用于表示无方向性关系的问题,例如社交网络中的好友关系、道路交通图等。
无向完全图:无向图中,任意两个顶点之间都存在边。
有向完全图:有向图中,任意两个顶点之间都存在方向互为相反的两条弧。
简单图:图中不存在顶点到其自身的边,且同一条边不重复出现。
稀疏图:有很少条边。
稠密图:有很多条边。
子图(Subgraph):假设G=(V,{E})和G‘=(V',{E'}),如果V'包含于V且E'包含于E,则称G'为G的子图。
边
边:顶点之间的逻辑关系用边来表示,边集可以是空的。
无向边(Edge):若顶点V1到V2之间的边没有方向,则称这条边为无向边。
无向图(Undirected graphs):图中任意两个顶点之间的边都是无向边。(A,D)=(D,A)
对于无向图G来说,G1=(V1,{E1}),其中顶点集合V1={A,B,C,D};边集和E1={(A,B),(B,C),(C,D),(D,A),(A,C)}

有向边:若从顶点V1到V2的边有方向,则称这条边为有向边,也称弧(Arc)。用<V1,V2>表示,V1为弧尾(Tail),V2为弧头(Head)。(V1,V2)≠(V2,V1)。
度
度是指与该顶点相邻的边的数量。

例如上图图中
-
A、B、C、E、F 这几个顶点度数为 2
-
D 顶点度数为 4
有向图中,细分为入度和出度,参见下图
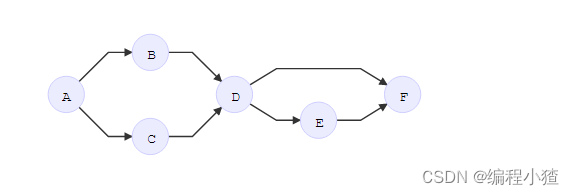
分析上图可知个顶点的出度与入度如下:
A (2 out / 0 in) 两个出度,没有入度
B、C、E (1 out / 1 in)
D (2 out / 2 in)
F (0 out / 2 in)
权
边可以有权重,代表从源顶点到目标顶点的距离、费用、时间或其他度量。

路径
路径被定义为从一个顶点到另一个顶点的一系列连续边,例如上图中【北京】到【上海】有多条路径。
北京 - 上海
北京 - 武汉 - 上海
路径长度
不考虑权重,长度就是边的数量
考虑权重,一般就是权重累加
环
在有向图中,从一个顶点开始,可以通过若干条有向边返回到该顶点,那么就形成了一个环。
如下图:

图的连通性
如果两个顶点之间存在路径,则这两个顶点是连通的,所有顶点都连通,则该图被称之为连通图,若子图连通,则称为连通分量。
graph LR
A --- B
A --- C
C --- D
D --- E
B --- E
F --- G
G --- H
H --- F
I --- J根据上面给出的点与点之间的连通性,可得出下图:

强连通分量:有向图中的极大强连通子图。
生成树:无向图中连通且n个顶点n-1条边叫生成树。
有向树:有向图中一顶点入度为0其余顶点入度为1。
森林:一个有向图由若干棵有向树构成生成森林。
图的表示方法
图可以用邻接矩阵和邻接表表示
比如说,下面的图

用邻接矩阵可以表示为:
A B C D A 0 1 1 0 B 1 0 0 1 C 1 0 0 1 D 0 1 1 0
用邻接表可以表示为:
A -> B -> C B -> A -> D C -> A -> D D -> B -> C
有向图的例子:
graph LR
A--->B
A--->C
B--->D
C--->D
用邻接矩阵可以表示为:
A B C D
A 0 1 1 0
B 0 0 0 1
C 0 0 0 1
D 0 0 0 0
用邻接表可以表示为:
A - B - C
B - D
C - D
D - empty
图的存储结构
邻接矩阵
邻接矩阵:用两个数组,一个数组保存顶点集,一个数组保存边集。
无向图
无向图的邻接矩阵如图

代码示例
我们先将表示顶点和边的类定义出来
假设顶点的类型为 Vertex:
class Vertex {
int value;
// 其他顶点属性
}假设边的类型为 Edge:
class Edge {
int startVertexId;
int endVertexId;
// 其他边属性
}class Graph {
Vertex[] vertices;
Edge[] edges;
int[][] adjacencyMatrix;
public Graph(Vertex[] vertices, Edge[] edges) {
this.vertices = vertices;
this.edges = edges;
this.adjacencyMatrix = new int[vertices.length][vertices.length];
// 初始化邻接矩阵,将相应位置设为 1 表示边的连接关系
for (Edge edge : edges) {
adjacencyMatrix[edge.startVertexId][edge.endVertexId] = 1;
// 如果是无向图还需要设置对称位置
adjacencyMatrix[edge.endVertexId][edge.startVertexId] = 1;
}
}
}有向图
有向图的邻接矩阵如图

代码示例
class Digraph {
Vertex[] vertices;
Edge[] edges;
int[][] adjacencyMatrix;
public Digraph(Vertex[] vertices, Edge[] edges) {
this.vertices = vertices;
this.edges = edges;
this.adjacencyMatrix = new int[vertices.length][vertices.length];
// 初始化邻接矩阵,将相应位置设为 1 表示边的连接关系
for (Edge edge : edges) {
adjacencyMatrix[edge.startVertexId][edge.endVertexId] = 1;
}
}
}邻接表
邻接表:数组与链表相结合的存储方法。
邻接表表示法(链式)表示如下图:

- 顶点: 按编号顺序将顶点数据存储在一维数组中。
- 关联同一顶点的边: 用线性链表存储。
- 如果有边\弧的信息,还可以在表结点中增加一项,

无向图
无向图的邻接表如下图:

特点:
- 邻接表不唯一
- 若无向图中有n个顶点、e条边,则其邻接表需要n个头结点和2e个表结点。适宜存储稀疏图。
- 无向图中顶点vi的度为第i个单链表中的结点数
代码示例
import java.util.ArrayList;
import java.util.List;
class Graph {
int numVertices;
List<List<Integer>> adjacencyList;
public Graph(int numVertices) {
this.numVertices = numVertices;
this.adjacencyList = new ArrayList<>(numVertices);
// 初始化邻接表
for (int i = 0; i < numVertices; i++) {
adjacencyList.add(new ArrayList<>());
}
}
public void addEdge(int src, int dest) {
// 添加双向边的连接关系
adjacencyList.get(src).add(dest);
adjacencyList.get(dest).add(src);
}
}
有向图

特点:
- 顶点vi的出度为第i个单链表中的结点个数。
- 顶点vi的入度为整个单链表中邻接点域值是i-1的结点个数。
- 找出度易,找入度难
逆邻接表:

逆邻接表特点:
- 顶点vi的入度为第i个单链表中的结点个数。
- 顶点vi的出度为整个单链表中邻接点域值是i-1的结点个数。
- 找入度易,找出度难。
当邻接表的存储结构形成后,图便唯一确定。
代码示例:
import java.util.ArrayList;
import java.util.List;
class Digraph {
int numVertices;
List<List<Integer>> adjacencyList;
public Digraph(int numVertices) {
this.numVertices = numVertices;
this.adjacencyList = new ArrayList<>(numVertices);
// 初始化邻接表
for (int i = 0; i < numVertices; i++) {
adjacencyList.add(new ArrayList<>());
}
}
public void addEdge(int src, int dest) {
// 添加单向边的连接关系
adjacencyList.get(src).add(dest);
}
}图的遍历
广度优先遍历(BFS)
广度优先遍历(Breadth First Search),又称为广度优先搜索,简称BFS。是一种分层的查找过程,每向前走一步可能访问一批顶点,不像深度优先搜索那样有往回退的情况,因此它不是一个递归的算法。为了实现逐层的访问,算法必须借助一个辅助队列,以记忆正在访问的顶点的下一层顶点。
其实他本意就是,先遍历一个节点,然后遍历那个节点所连接的的周边节点,之后再一个结点一个结点的往外遍历,重复循环。
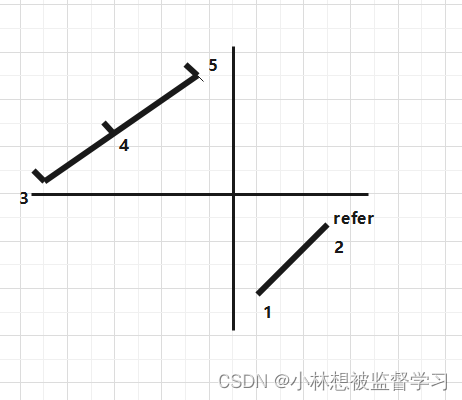
下面举个例子:

这张图,我们设从“3”开始遍历,运用广度优先的方法,那么我们所得到的遍历顺序为3,2,3,4,5,1
深度优先遍历(DFS)
所谓DFS,就是从起点开始,找准一个方向直到走不了为止,然后再原路返回,再找到一个能走的地方继续走的思路。
下面举个例子:
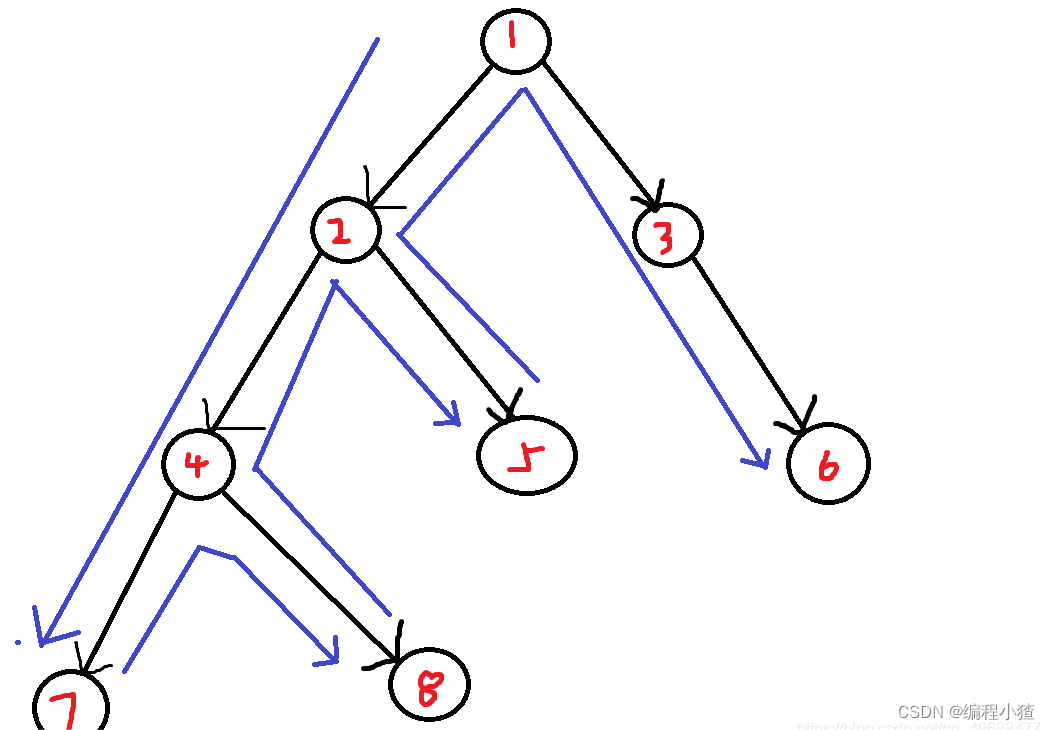
遍历顺序为:1,2,4,7,8,5,3,6
这里这两种算法,我只是概述一下,后面我还会写两篇博文来专门讲这两种遍历方式
上面差不多就是刷图论的题所需要具备的图的基础知识了,后续我会继续更新一些我在刷图论题的一些体会。