回溯算法第三篇（批处理作业调度、N皇后【基于排列树实现】、符号三角形问题）

1. 批处理作业调度

2. N皇后【基于排列树实现】

3. 符号三角形问题

1. 批处理作业调度

题目描述：给定n个作业的集合 $J = \left ( J_{1},J_{2} ,\cdots,J_{n}\right )$ 。每个作业 $J_{i}$ 都有两项任务分别在两台机器上完成。每个作业必须先由机器1处理，再由机器2处理。作业 $J_{i}$ 需要机器j的处理时间为 $jobs_{ji}\left ( i = 1,2,\cdots ,n; j=1,2 \right )$ 。对于一个确定的作业调度，设 $F_{ji}$ 是作业i在机器j上完成处理的时间，则所有作业在机器2上完成处理的时间和 $f=\sum_{i=1}^{n}F_{2i}$ 称为该作业调度的完成时间和。

题目解析：

（1）批处理作业调度问题要求，对于给定的 n 个作业，制定最佳作业调度方案，使其完成时间和达到最小。

（2）批处理作业调度问题的一个常见例子是，在计算机系统中完成一批 n 个作业，每个作业都要先完成计算，然后将计算结果打印输出。计算任务由计算机的中央处理器是机器1，打印机是机器2。

（3）调度必须遵循两点：

一个作业必须先由机器1处理，再由机器2处理，顺序不可颠倒；
机器1处理n个作业的顺序必须和机器2处理n个作业的顺序相同（因为只有这样才能使作业调度的完成时间和最小）

（4）由于作业调度就是一个先后顺序的改变，所以解决这一类问题的决策树是排列树。

具体举例如下：

如下图，给出了3个作业分别需要机器1和机器2的处理时间，试给出一种调度方案，使该作业调度的完成时间和最小。

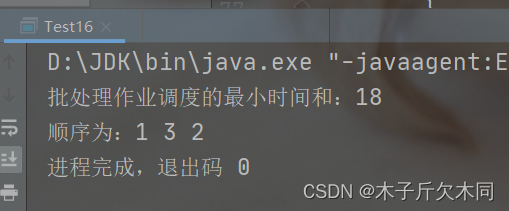
3个作业可能的调度顺序有6种：1→2→3、1→3→2、2→1→3、2→3→1、3→1→2、3→2→1。经过计算，它们的完成时间和对应为：19、18、20、21、19、19，因此最佳调度方案为1→3→2，其完成时间和为18。

以1→3→2，其完成时间和为18为例子，

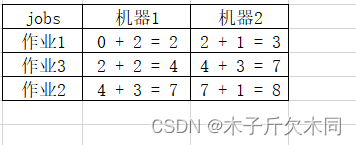
结果：3 + 7 + 8 = 18。

注意：一个作业在第2台机器上开始的时间，是取决于上一个作业在机器2上完成的时间和自己本身在机器1上完成的时间的最大值。

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

public class Test16 {
    /*
    定义一批作业
    （1）第一维度表示作业1,2,3
    （2）第二维度表示在机器1,还是机器2上运行的时间
     */
    int N = 3;//表示有三个作业需要调度
    int[][] jobs = {{2, 1}, {3, 1}, {2, 3}};
    boolean[] isJobsRun;
    int minTime = Integer.MAX_VALUE;//表示最小的运行时间
    int[] nowRun;//表示当前的机器的运行顺序
    int[] jobsRun;//表示最佳机器的运行顺序

    public void permute(int[][] jobs) {
        //1.初始化
        isJobsRun = new boolean[jobs.length];
        jobsRun = new int[jobs.length];
        nowRun = new int[jobs.length];
        Arrays.fill(nowRun, -1);
        //2.调用dfs(回溯的核心)
        dfs(0);
    }

    public void dfs(int t) {
        //当来到叶子节点后，就进行时间累加
        if (t == N) {
            int t1 = 0, t2 = 0, sum = 0;
            for (int x = 0; x < N; x++) {
                int i = nowRun[x];
        //一个作业在第2台机器上开始的时间，
        //是取决于上一个作业在机器2上完成的时间和自己本身在机器1上完成的时间的最大值
                t1 = t1 + jobs[i][0];
                t2 = Math.max(t1, t2) + jobs[i][1];
                //sum就是在累加没一个作业最后再机器2上完成的时间和
                sum += t2;
            }
            int tmpTime = minTime;//用来判断是否有最小值的改变
            minTime = Math.min(minTime, sum);
            //如果两者不相等，正面值有进行改变
            if (tmpTime != minTime) {
                //将本次的机器运转顺序记录下来
                for (int i = 0; i < N; i++) {
                    jobsRun[i] = nowRun[i] + 1;
                }
            }
        }
        //如果
        else {
            //每次都从第一个机器开始看起
            for (int i = 0; i < N; i++) {
                //证明这个作业没被选择
                if (isJobsRun[i] == false) {
                    //把这个作业标记为已选择
                    isJobsRun[i] = true;
                    //因为下标是从0开始，所以第1个作业就是 0 ;
                    nowRun[t] = i;
                    dfs(t + 1);
                    //恢复现场
                    isJobsRun[i] = false;
                    nowRun[t] = -1;
                }
            }
        }
    }

    public static void main(String[] args) {
        Test16 test16 = new Test16();
        test16.permute(test16.jobs);
        System.out.println(test16.minTime);
        for(int i = 0;i < test16.N;i++){
            System.out.println(test16.jobsRun[i] + " ");
        }
    }
}

2. N皇后【基于排列树实现】

题目描述：按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

解决方案如下：（建议配合全部代码一起看）

（1）算法思路（假设是 4 皇后）

    static int N;//皇后数量、行或者列的大小
    static int[] queenLocal;//表示皇后所在的位置，数组下标表示行，数组里面存储的值表示列

    queenLocal = new int[N];
    //让皇后们先按对角线排列
    for (int i = 0; i < queenLocal.length; i++) {
         queenLocal[i] = i;
    }

因为我们是基于排列树实现N皇后，根据N皇后的题目要求，每一行只能有一个皇后，则先让4个皇后按对角线先排好队，然后改变每一行皇后在每一列的不同位置可以得到的结果是否满足题意，若满足就是一种排列方式，进行output打印。

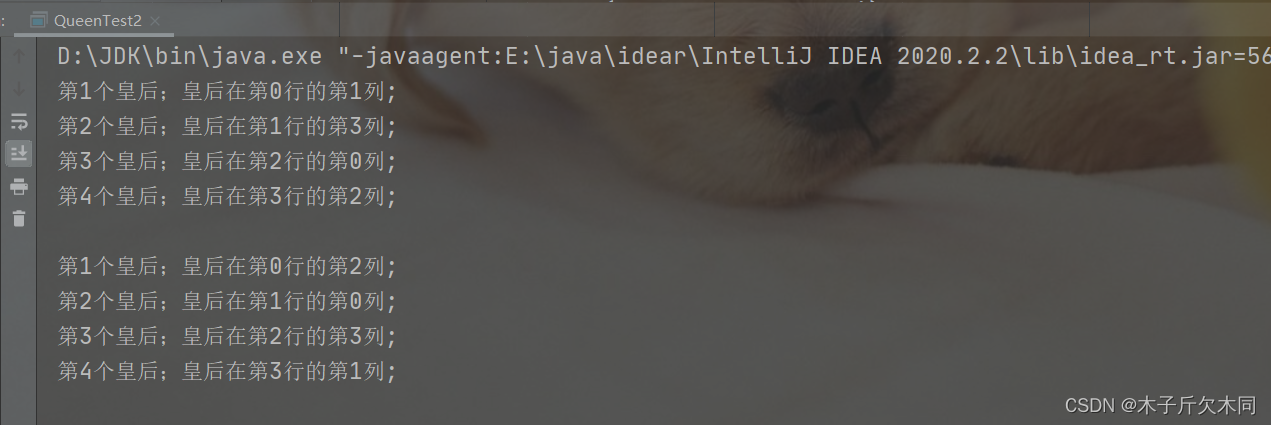
    //满足条件来到output方法，打印皇后们的所在位置
    public static void output() {
        for (int i = 0; i < N; i++) {
            System.out.println("第" + (i + 1) + "个皇后；" 
                    + "皇后在第" + i + "行的第" + queenLocal[i] + "列;");
        }
        System.out.println();
    }

（2）核心代码

   public static void dfs(int row) {
        //证明已经排列到最后一行了
        if (row == N) {
            output();
        } else {
            for (int i = row; i < N; i++) {
                //row表示当前序列的首位元素的下标
                //交换位置，最终达到排列顺序的改变，其实就是不断的改变居于首位的元素
                swap(queenLocal, row, i);
                if (legal(row)) {
                    //去往下一行，也可以理解为下一个元素，然后还是一样
                    //不断改变首位的元素，判断是否合法，合法就继续去往下一行
                    //或者说去判断下一个元素的合理性
                    dfs(row + 1);
                }
                //恢复现场：之前改变了首元素的位置，现在要还原，不然下次再改变首位置元素就会错乱
                swap(queenLocal, row, i);
            }
        }
    }

    //交换数据的代码
    public static void swap(int[] a, int i, int j) {
        int tmp = a[i];
        a[i] = a[j];
        a[j] = tmp;
    }

全部代码：


//基于排列树实现N皇后
public class QueenTest2 {
    static int N;//皇后数量、行或者列的大小
    static int[] queenLocal;//表示皇后所在的位置，数组下标表示行，数组里面存储的值表示列

    //交换数据的代码
    public static void swap(int[] a, int i, int j) {
        int tmp = a[i];
        a[i] = a[j];
        a[j] = tmp;
    }

    //进行位置是否合法的判断
    public static boolean legal(int row) {
        for (int i = 0; i < row; i++) {
            //第一个条件判断列是不是相同，是不是在不同行，已经选了同一列
            //有两种规律（1）行减行，列减列两值相等；（2）每条对角线行列相减都有各自的定值
            if (queenLocal[i] == queenLocal[row] ||
                    Math.abs(row - i) == Math.abs(queenLocal[row] - queenLocal[i])) {
                return false;
            }
        }
        return true;
    }

    //传入参数是第几行的意思
    //row表示从第几行开始算起；num表示几皇后
    public static void permute(int row, int num) {
        //1.初始化
        N = num;
        queenLocal = new int[N];
        //让皇后们先按对角线排列
        for (int i = 0; i < queenLocal.length; i++) {
            queenLocal[i] = i;
        }
        //2.开始回溯
        dfs(row);
    }

    //满足条件来到output方法，打印皇后们的所在位置
    public static void output() {
        for (int i = 0; i < N; i++) {
            System.out.println("第" + (i + 1) + "个皇后；"
                    + "皇后在第" + i + "行的第" + queenLocal[i] + "列;");
        }
        System.out.println();
    }

    public static void dfs(int row) {
        //证明已经排列到最后一行了
        if (row == N) {
            output();
        } else {
            for (int i = row; i < N; i++) {
                //row表示当前序列的首位元素的下标
                //交换位置，最终达到排列顺序的改变，其实就是不断的改变居于首位的元素
                swap(queenLocal, row, i);
                if (legal(row)) {
                    dfs(row + 1);
                }
                //恢复现场：之前改变了首元素的位置，现在要还原，不然下次再改变首位置元素就会错乱
                swap(queenLocal, row, i);
            }
        }
    }

    public static void main(String[] args) {
        //我这里用4皇后举例，只需要改变传入的num参数，就可以实现不同的皇后效果
        permute(0, 4);
    }
}

3. 符号三角形问题

题目描述：图是由14个“+”和14个“-”组成的符号三角形。两个同号下面都是“+”，两个异号下面都是“-”。在一般情况下，符号三角形的第一行有n个符号。符号三角问题要求对于给定的n，计算有多少个不同的符号三角形，使其所含的“+”和“-”的个数相同。如下图所示：

解决方案如下：为了方便计算，先把上图的三角形变化成如下的三角形，在打印的时候，再将下列数组的打印成如上图所示。

上图所提到的内容，在代码上会体现，注意理解！！！

根据题意：其实就是对第一行进行全排列，只要能来到第一行的最后一列，这就是其中一种情况，根据这种情况生成下面 N - 1 行的字符即可，最后记录“+”和“-”的数量，看是否满足条件即可！！！

public class TriangleTest {
    static int N = 7;//表示行和列都是7
    static char[][] triangle;//用来存放每次+和-的位置

    public static void permute() {
        //1.初始化
        triangle = new char[N][N];
        //2.回溯的核心
        dfs(0);
    }

    //判断是否满足"+"和"-"的数量是否满足题意
    public static boolean isSameTriangle() {
        int sumPlus = 0;//用来记录 + 的个数
        int sumSub = 0;//用来记录 - 的个数
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < N - i; j++) {
                if (triangle[i][j] == '+')
                    sumPlus++;
                if (triangle[i][j] == '-')
                    sumSub++;
            }
        }
        //如果两者相等，返回true，证明满足题意
        if (sumPlus == sumSub)
            return true;
        return false;
    }

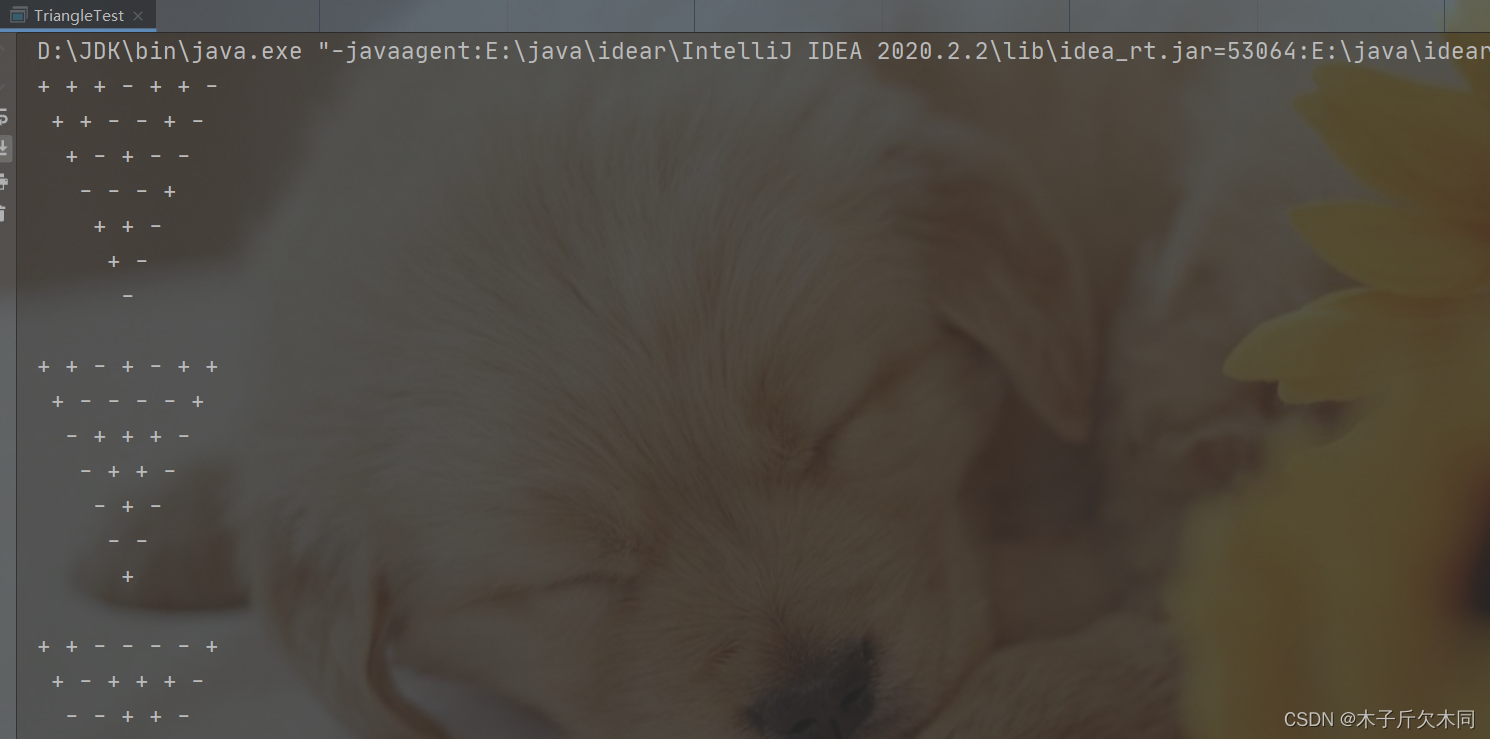
    //打印满足题意的三角形
    public static void printfTriangle() {
        for (int i = 0; i < N; i++) {
            //打印三角形前面的空白
            for (int x = 0; x < i; x++) {
                System.out.print(" ");//打印一个空格
            }
            //打印字符
            for (int j = 0; j < N - i; j++) {
                System.out.print(triangle[i][j] + " ");
            }
            //换行
            System.out.println();
        }
        System.out.println();
    }

    //排列到第一行的最后一列元素，开始进行构造三角形
    public static void output() {
        /*
        能进入这个方法，证明第一行已经排好了，
        所以从第二行第一列开始填充
         */
        for (int i = 1; i < N; i++) {
            //这个在上图有解释
            for (int j = 0; j < N - i; j++) {
                //两个同号下面都是“+”，两个异号下面都是“-”。
                triangle[i][j] = triangle[i - 1][j] == triangle[i - 1][j + 1]
                        ? '+' : '-';
            }
        }
        //判断是否满足"+"和"-"的数量都是14！
        //满足题意，就打印三角形
        if (isSameTriangle()) {
            printfTriangle();
        }
    }

    //这题的回溯核心代码
    public static void dfs(int col) {
        //能进入if，证明第一行的字符已经排列完了
        if (col == N) {
            output();
        } else {
            //第一行的col是 +
            triangle[0][col] = '+';
            //递归看第一行的下一列
            dfs(col + 1);

            //第一行的col是 -
            triangle[0][col] = '-';
            //递归看第一行的下一列
            dfs(col + 1);
        }
    }

    public static void main(String[] args) {
        permute();
    }
}