🍊作者简介：秃头小苏，致力于用最通俗的语言描述问题

🍊专栏推荐：深度学习网络原理与实战

🍊近期目标：写好专栏的每一篇文章

🍊支持小苏：点赞👍🏼、收藏⭐、留言📩

 

 

Diffusion Model原理详解及源码解析

写在前面

Hello，大家好，我是小苏🧒🏽🧒🏽🧒🏽

  今天来为大家介绍Diffusion Model（扩散模型 ），在具体介绍之前呢，先来谈谈Diffusion Model主要是用来干什么的。🥂🥂🥂其实啊，它对标的是生成对抗网络（GAN），只要GAN能干的事它基本都能干。🍄🍄🍄在之前我已经做过很多期有关GAN网络的教学，还不清楚的可以点击☞☞☞进入专栏查看详情。在我一番体验Diffusion Model后，它给我的感觉是非常惊艳的。我之前用GAN网络来实现一些图片生成任务其实效果并不是很理想，而且往往训练很不稳定。但是换成Diffusion Model后生成的图片则非常逼真，也明显感觉到每一轮训练的结果相比之前都更加优异，也即训练更加稳定。

  说了这么多，我就是想告诉大家Diffusion Model值得一学。🍋🍋🍋但是说实话，这部分的公式理解起来是有一定困难的，我想这也成为了想学这个技术的同学的拦路虎。那么本文将用通俗的语言和公式为大家介绍Diffusion Model，并且结合公式为大家梳理Diffusion Model的代码，探究其是如何通过代码实现的。如果你想弄懂这部分，请耐心读下去，相信你会有所收获。🌾🌾🌾

如果你准备好了的话，就让我们开始吧！！！🚖🚖🚖

 

Diffusion Model原理详解✨✨✨

整体思路

Diffusion Model的整体思路如下图所示：

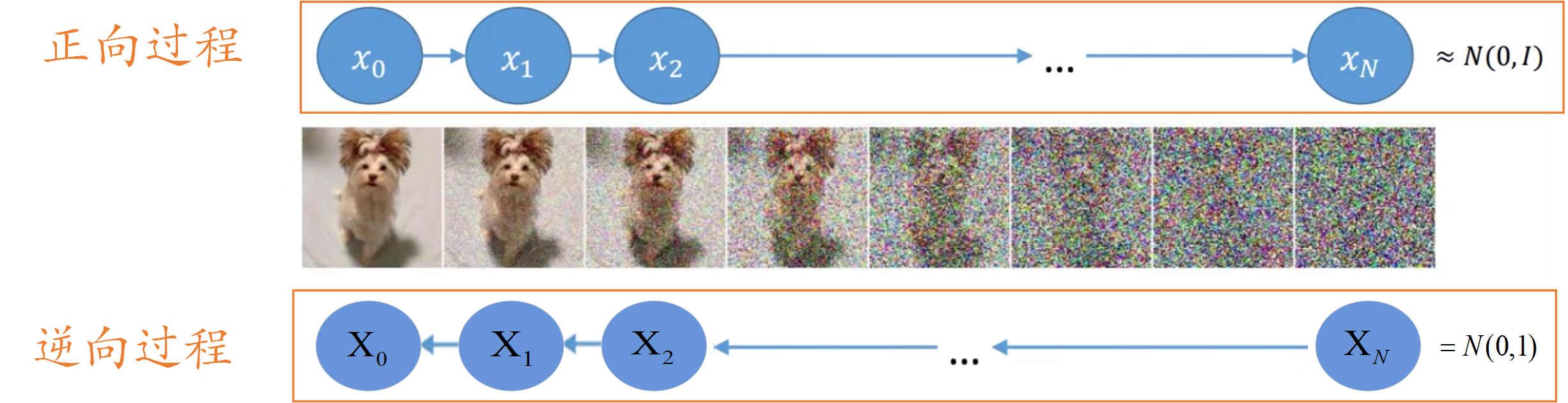
其主要分为正向过程和逆向过程，正向过程类似于编码，逆向过程类似于解码。

• 正向过程

  首先，对于一张原始图片$x_0$，我们给$x_0$加一个高斯噪声，图片由$x_0$变成$x_1$。【注意：这里必须要加高斯噪声喔，因为高斯噪声服从高斯分布，后面的一些运算需要用到高斯分布的一些特性】接着我们会在$x_1$的基础上再添加高斯噪声得到$x_2$。重复上述添加高斯噪声步骤，直到图片变成$x_n$，由于添加了足够多的高斯噪声，现在的$x_n$近似服从高斯分布（又称正态分布）。

  现在有一个问题需要大家思考一下，我们每一步添加高斯噪声的量一直是不变的吗？🎅🏽🎅🏽🎅🏽滴，开始解答。答案是每步添加高斯噪声的量是变化的，且后一步比前一步添加的高斯噪声更多。我想这一点你通过上图也非常容易理解，一开始原图比较干净，我们添加少量高斯噪声就能对原图产生干扰；但越往后高斯噪声量越多，如果还添加一开始少量的高斯噪声，那么这时对上一步结果基本不会产生任何影响。【注：后文所述的每个时刻图像和这里的每一步图像都是一个意思，如$x_1$时刻图像表示的就是$x_1$这个图像】

• 逆向过程

  首先，我们会随机生成一个服从高斯分布的噪声图片，然后一步一步的减少噪声直到生成预期图片。逆向过程大家先有这样的一个认识就好，具体细节稍后介绍。🌱🌱🌱

怎么样，大家现在的感觉如何？是不是知道了Diffusion Model大概是怎么样的过程了呢，但是又对里面的细节感到很迷惑，搞不懂这样是怎么还原出图片的。不用担心，后面我会慢慢为大家细细介绍。🥡🥡🥡

 

实施细节

  这一部分为大家介绍一下Diffusion Model正向过程和逆向过程的细节，主要通过推导一些公式来表示加噪前后图像间的关系，谈到公式，大家可能头都大了，相信我，你可以看懂！！！🥂🥂🥂

正向过程

  在整体思路部分我们已经知道了正向过程其实就是一个不断加噪的过程，于是我们考虑能不能用一些公式表示出加噪前后图像的关系呢。我想让大家先思考一下后一时刻的图像受哪些因素影响呢，更具体的说，比如$x_2$由哪些量所决定呢？我想这个问题很简单，即$x_2$是由$x_1$和所加的噪声共同决定的，也就是说后一时刻的图像主要由两个量决定，其一是上一时刻图像，其二是所加噪声量。【这个很好理解，大家应该都能明白吧】明白了这点，我们就可以用一个公式来表示$x_t$时刻和$x_{t-1}$时刻两个图像的关系，如下：

              $X_t=\sqrt{a_t}{X}_{t-1}+\sqrt{1-a_t}{Z}_1$     ——公式1

  其中，$X_t$表示$t$时刻的图像，$X_{t-1}$表示$t-1$时刻图像，$Z_1$表示添加的高斯噪声，其服从N(0,1)分布。【注：N(0,1)表示标准高斯分布，其方差为1，均值为0】目前你可以看出$X_t$和$X_{t-1}$、$Z_1$都有关系，这和我们前文所述后一时刻的图像由前一时刻图像和噪声决定相符合，这时你可能要问了，那么这个公式前面的$\sqrt{a_t}$和$\sqrt{1-a_t}$是什么呢，其实这个表示这两个量的权重大小，它们的平方和为1。

  enmmm，我想你已经明白了公式1，但是你可能对$\sqrt{a_t}$和$\sqrt{1-a_t}$的理解还存在一些疑惑，如为什么要设置这样的权重？这个权重的设置是我们预先设定的吗？🌶🌶🌶其实呢，$a_t$还和另外一个量${\beta }_t$有关，关系式如下：

​              $a_t=1-{\beta }_t$      ——公式2

  其中，${\beta }_t$是预先给定的值，它是一个随时刻不断增大的值，论文中它的范围为[0.0001,0.002]。既然${\beta }_t$越来越大，则$a_t$越来越小，$\sqrt{a_t}$越来越小，$\sqrt{1-a_t}$越来越大。现在我们在来考虑公式1，$Z_1$的权重$\sqrt{1-a_t}$随着时刻增加越来越大，表明我们所加的高斯噪声越来越多，这和我们整体思路部分所述是一致的，即越往后所加的噪声越多。🍄🍄🍄

---

  现在，我们已经得到了$x_t$时刻和$x_{t-1}$时刻两个图像的关系，但是$x_{t-1}$时刻的图像是未知的。【注：只有$x_0$阶段图像是已知的，即原图】我们需要再由$x_{t-2}$时刻推导出$x_{t-1}$时刻图像，然后再由$x_{t-3}$时刻推导出$x_{t-2}$时刻图像，依此类推，直到由$x_0$时刻推导出$x_1$时刻图像即可。既然这样我们不妨先试试$x_{t-2}$时刻图像和$x_{t-1}$时刻图像的关系，如下：

​             $X_{t-1}=\sqrt{a_{t-1}}{X}_{t-2}+\sqrt{1-a_{t-1}}{Z}_2$      ——公式3

这个公式很简单吧，就是公式1的一个类推公式，此时我们将公式3代入公式1中得：

​        $\begin{array}{l}{X}_t=\sqrt{a_t}(\sqrt{a_{t-1}}{X}_{t-2}+\sqrt{1-a_{t-1}}{Z}_2)+\sqrt{1-a_t}{Z}_1\\ =\sqrt{a_t{a}_{t-1}}{X}_{t-2}+\sqrt{a_t(1-a_{t-1})}{Z}_2+\sqrt{1-a_t}{Z}_1\\ =\sqrt{a_t{a}_{t-1}}{X}_{t-2}+\sqrt{1-a_t{a}_{t-1}}{\hat{Z}}_2\end{array}$      ——公式4

这个公式4大家能理解吗？🌼🌼🌼我觉得大家应该对最后一个等式存在疑惑，也即$\sqrt{a_t(1-a_{t-1})}{Z}_2+\sqrt{1-a_t}{Z}_1$怎么等于$\sqrt{1-a_t{a}_{t-1}}{\hat{Z}}_2$ ？其实呢，这个用到了高斯分布的一些知识，这部分见附录部分，我做相关介绍。看了附录中高斯分布的相关性质，我想这里你应该能够理解了，我在帮大家整理一下，如下图所示：

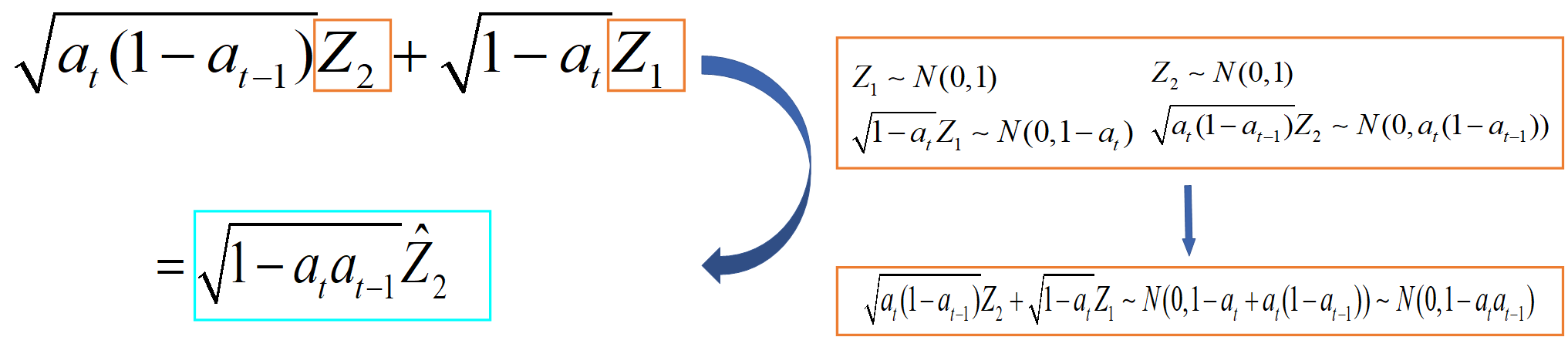
这下对于公式4的内容都明白了叭。注意这里的${\hat{Z}}_2$也是服从$N(0,1)$高斯分布的，$\sqrt{a_t(1-a_{t-1})}{Z}_2+\sqrt{1-a_t}{Z}_1$服从$N(0,1-a_t{a}_{t-1})$。我们来看看公式4得到了什么——其得到了$x_t$时刻图像和$x_{t-2}$时刻图像的关系。按照我们先前的理解，我们再列出$x_{t-3}$时刻图像和$x_{t-2}$时刻图像的关系，如下：

​              $X_{t-2}=\sqrt{a_{t-2}}{X}_{t-3}+\sqrt{1-a_{t-2}}{Z}_3$     ——公式5

同理，我们将公式5代入到公式4中，得到$x_t$时刻图像和$x_{t-3}$时刻图像的关系，公式如下：

​            $X_t=\sqrt{a_t{a}_{t-1}{a}_{t-2}}{X}_{t-3}+\sqrt{1-a_t{a}_{t-1}{a}_{t-2}}{\hat{Z}}_3$      ——公式6

  公式5我没有带大家一步步的计算了，只写出了最终结果，大家可以自己算一算，非常简单，也只用到了高斯分布的相关性质。注意上述的$\widehat{Z_3}$同样服从$N(0,1)$的高斯分布。那么公式6就得到了$x_t$时刻图像和$x_{t-3}$时刻图像的关系，我们如果这么一直计算下去，就会得到$x_t$时刻图像和$x_0$时刻图像的关系。但是这样的推导貌似很漫长，随着向后推导你会发现这种推导是有规律的。我们可以来比较一下公式4和公式6的结果，你会发现很明显的规律，这里我就根据这个规律直接写出$x_t$时刻图像和$x_0$时刻图像的关系，你看看和你想的是否一致喔，公式如下：

​              $X_t=\sqrt{{\bar{a}}_t}{X}_0+\sqrt{1-{\bar{a}}_t}{\hat{Z}}_t$      ——公式7

  其中${\bar{a}}_t$表示累乘操作，即${\bar{a}}_t=a_t\cdot a_{t-1}\cdot a_{t-2}\cdots a_1$ ，${\hat{Z}}_t$同样服从$N(0,1)$的高斯分布。【这里${\hat{Z}}_t$只是一个表示，只要$Z$服从标准高斯分布即可，用什么表示都行】这个公式7就是整个正向过程的核心公式喔，其表示$x_t$时刻的图像可以由$x_0$时刻的图像和一个标准高斯噪声表示，大家需要牢记这个公式哦，在后文以及代码中会用到。🍈🍈🍈

---

逆向过程

  逆向过程是将高斯噪声还原为预期图片的过程。先来看看我们已知条件有什么，其实就一个$x_t$时刻的高斯噪声。我们希望将$x_t$时刻的高斯噪声变成$x_0$时刻的图像，是很难一步到位的，因此我们思考能不能和正向过程一样，先考虑$x_t$时刻图像和$x_{t-1}$时刻的关系，然后一步步向前推导得出结论呢。好的，思路有了，那就先来想想如何由已知的$x_t$时刻图像得到$x_{t-1}$时刻图像叭。🥂🥂🥂

  有没有大佬想出怎么办呢？我就不卖关子了，要想由$x_t$时刻图像得到$x_{t-1}$时刻图像，我们需要利用正向过程中的结论，我们在正向过程中可以由$x_{t-1}$时刻图像得到$x_t$时刻图像，然后利用贝叶斯公式即可求解。

  ！！！？？？什么，贝叶斯公式，不知道大家是否了解。如果不知道的建议去学习一下概率的知识，如果实在也不想学，大家就记住贝叶斯公式的表达式即可，如下：

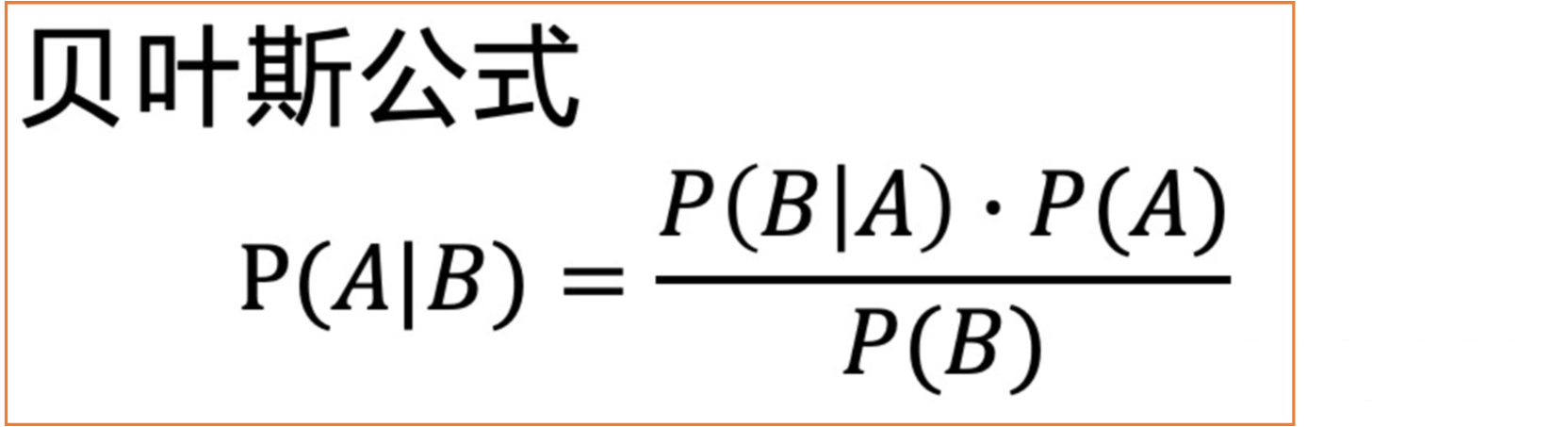
那么我们将利用贝叶斯公式来求$x_{t-1}$时刻图像，公式如下：

​              $q(X_{t-1}|X_t)=q(X_t|X_{t-1})\frac{q(X_{t-1})}{q(X_t)}$     ——公式8

  公式8中$q(X_t|X_{t-1})$我们可以求得，就是刚刚正向过程求的嘛。🍟🍟🍟但$q(X_{t-1})$和$q(X_t)$是未知的。又由公式7可知，可由$X_0$得到每一时刻的图像，那当然可以得到$X_t$和$X_{t-1}$时刻的图像，故将公式8加一个$X_0$作为已知条件，将公式8变成公式9，如下：

​            $q(X_{t-1}|X_t,X_0)=q(X_t|X_{t-1},X_0)\frac{q(X_{t-1}|X_0)}{q(X_t|X_0)}$     ——公式9

  现在可以发现公式9右边3项都是可以算的啦，我们列出它们的公式和对应的分布，如下图所示：

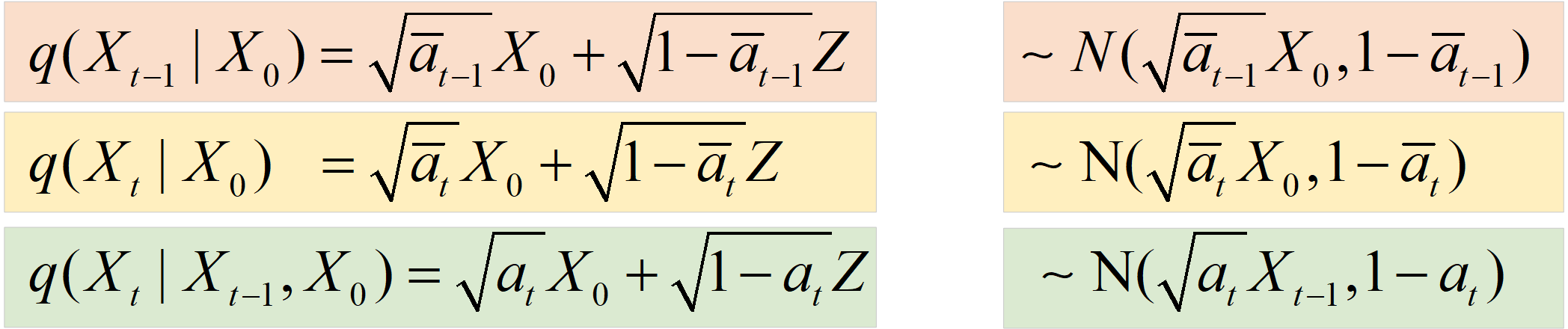
  知道了公式9等式右边3项服从的分布，我们就可以计算出等式左边的$q(X_{t-1}|X_t,X_0)$。大家知道怎么计算嘛，这个很简单啦，没有什么技巧，就是纯算。在附录->高斯分布性质部分我们知道了高斯分布的表达式为：$f(x)=\frac{1}{\sqrt{2\pi \sigma }}{e}^{-\frac{{(x-u)}^2}{2{\sigma }^2}}$。那么我们只需要求出公式9等式右边3个高斯分布表达式，然后进行乘除运算即可求得$q(X_{t-1}|X_t,X_0)$。

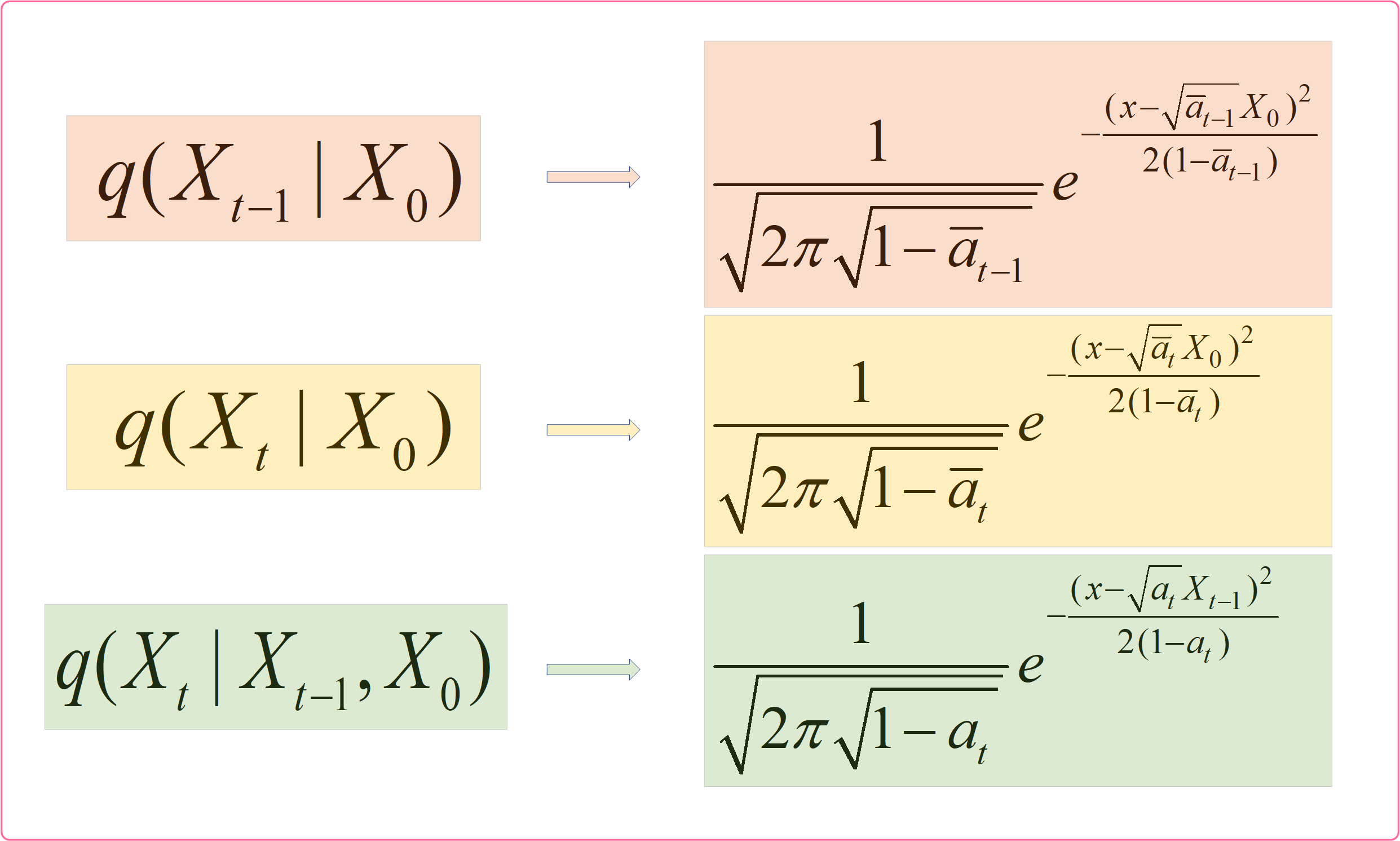
  上图为等式右边三个高斯分布表达式，这个结果怎么得的大家应该都知道叭，就是把各自的均值和方差代入高斯分布表达式即可。现我们只需对上述三个式子进行对应乘除运算即可，如下图所示：

  好了，我们上图中得到了式子$M\cdot e^{-\frac{1}{2}[(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{a}}_{t-1}})X_{t-1}^2-(\frac{2\sqrt{{\bar{a}}_t}}{{\beta }_t}{X}_t+\frac{2\sqrt{{\bar{a}}_{t-1}}}{1-{\bar{a}}_{t-1}}{X}_0)X_{t-1}+C(X_t,X_0)]}$其实就是$q(X_{t-1}|X_t)$的表达式了。知道了这个表达式有什么用呢，主要是求出均值和方差。首先我们应该知道对高斯分布进行乘除运算的结果仍然是高斯分布，也就是说$q(X_{t-1}|X_t)$服从高斯分布，那么他的表达式就为 $f(x)=\frac{1}{\sqrt{2\pi \sigma }}{e}^{-\frac{{(x-u)}^2}{2{\sigma }^2}}=\frac{1}{\sqrt{2\pi \sigma }}{e}^{-\frac{1}{2}[\frac{x^2}{{\sigma }^2}-\frac{2ux}{{\sigma }^2}+\frac{u^2}{{\sigma }^2}]}$，我们对比两个表达式，就可以计算出$u$和${\sigma }^2$，如下图所示：

  现在我们有了均值$u$和方差${\sigma }^2$就可以求出$q(X_{t-1}|X_t)$了，也就是求得了$x_{t-1}$时刻的图像。推导到这里不知道大家听懂了多少呢？其实你动动小手来算一算你会发现它还是很简单的。但是不知道大家有没有发现一个问题，我们刚刚求得的最终结果$u$和${\sigma }^2$中含义一个$X_0$，这个$X_0$是什么啊，他是我们最后想要的结果，现在怎么当成已知量了呢？这一块确实有点奇怪，我们先来看看我们从哪里引入了$X_0$。往上翻翻你会发现使用贝叶斯公式时我们利用了正向过程中推导的公式7来表示$q(X_{t-1})$和$q(X_t)$，但是现在看来那个地方会引入一个新的未知量$X_0$，该怎么办呢？这时我们考虑用公式7来反向估计$X_0$，即反解公式7得出$X_0$的表达式，如下：

​              $X_0=\frac{1}{\sqrt{{\bar{a}}_t}}(X_t-\sqrt{1-{\bar{a}}_t}{\hat{Z}}_t)$      ——公式10

得到$X_0$的估计值，此时将公式10代入到上图的$u$中，计算后得到最后估计的 $\tilde{u}$，表达式如下：

​              $\tilde{u}=\frac{1}{\sqrt{a_t}}(x_t-\frac{{\beta }_t}{\sqrt{1-{\bar{a}}_t}}{\hat{Z}}_t)$      ——公式11

好了，现在在整理一下$t-1$时刻图像的均值$u$和方差${\sigma }^2$，如下图所示：

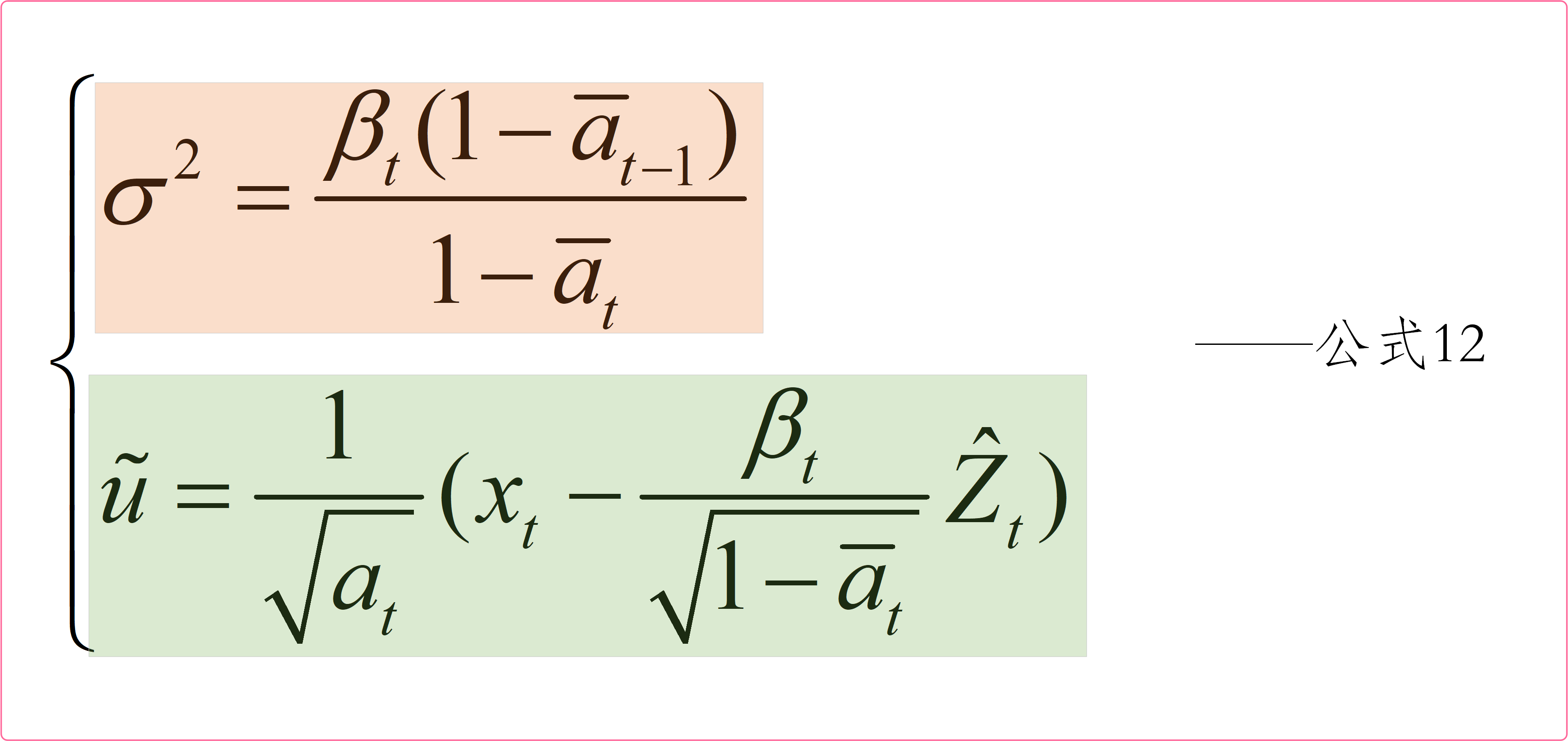
有了公式12我们就可以估计出$X_{t-1}$时刻的图像了，接着就可以一步步求出$X_{t-2}$、$X_{t-3}$、$X_1$、$X_0$的图像啦。🍄🍄🍄🍄

---

原理小结

  这一小节原理详解部分就为大家介绍到这里了，大家听懂了多少呢。相信你阅读了此部分后，对Diffusion Model的原理其实已经有了哥大概的解了，但是肯定还有一些疑惑的地方，不用担心，代码部分会进一步帮助大家。🌸🌸🌸

 
 

Diffusion Model源码解析✨✨✨

代码下载及使用

  本次代码下载地址：Diffusion Model代码🚀🚀🚀

  先来说说代码的使用吧，代码其实包含两个项目，一个的ddpm.py，另一个是ddpm_condition.py。大家可以理解为ddpm.py是最简单的扩散模型，ddpm_condition.py是ddpm.py的优化。本节会以ddpm.py为大家讲解。代码使用起来非常简单，首先在ddpm.py文件中指定数据集路径，即设置dataset_path的值，然后我们就可以运行代码了。需要注意的是，如果你使用的是CPU的话，那么你可能还需要修改一下代码中的device参数，这个就很简单啦，大家自己摸索摸索就能研究明白。

---

  这里来简单说说ddpm的意思，英文全称为Denoising Diffusion Probabilistic Model，中文译为去噪扩散概率模型。🍄🍄🍄

---

代码流程图

这里我们直接来看论文中给的流程图好了，如下：

  看到这个图你大概率是懵逼的，我来稍稍为大家解释一下。首先这个图表示整个算法的流程分为了训练阶段（Training）和采样阶段（Sampling）。

• Training

  我们先来看看训练阶段我们做了什么？众所周知，训练我们需要有真实值和预测值，那么对于本例的真实值和预测值是什么呢？真实值是我们输入的图片，预测值是我们输出的图片吗？其实不是，这里我就不和大家卖关子了。对于本例来说，真实值和预测值都是噪声，我们同样拿下图为大家做个示范。

  

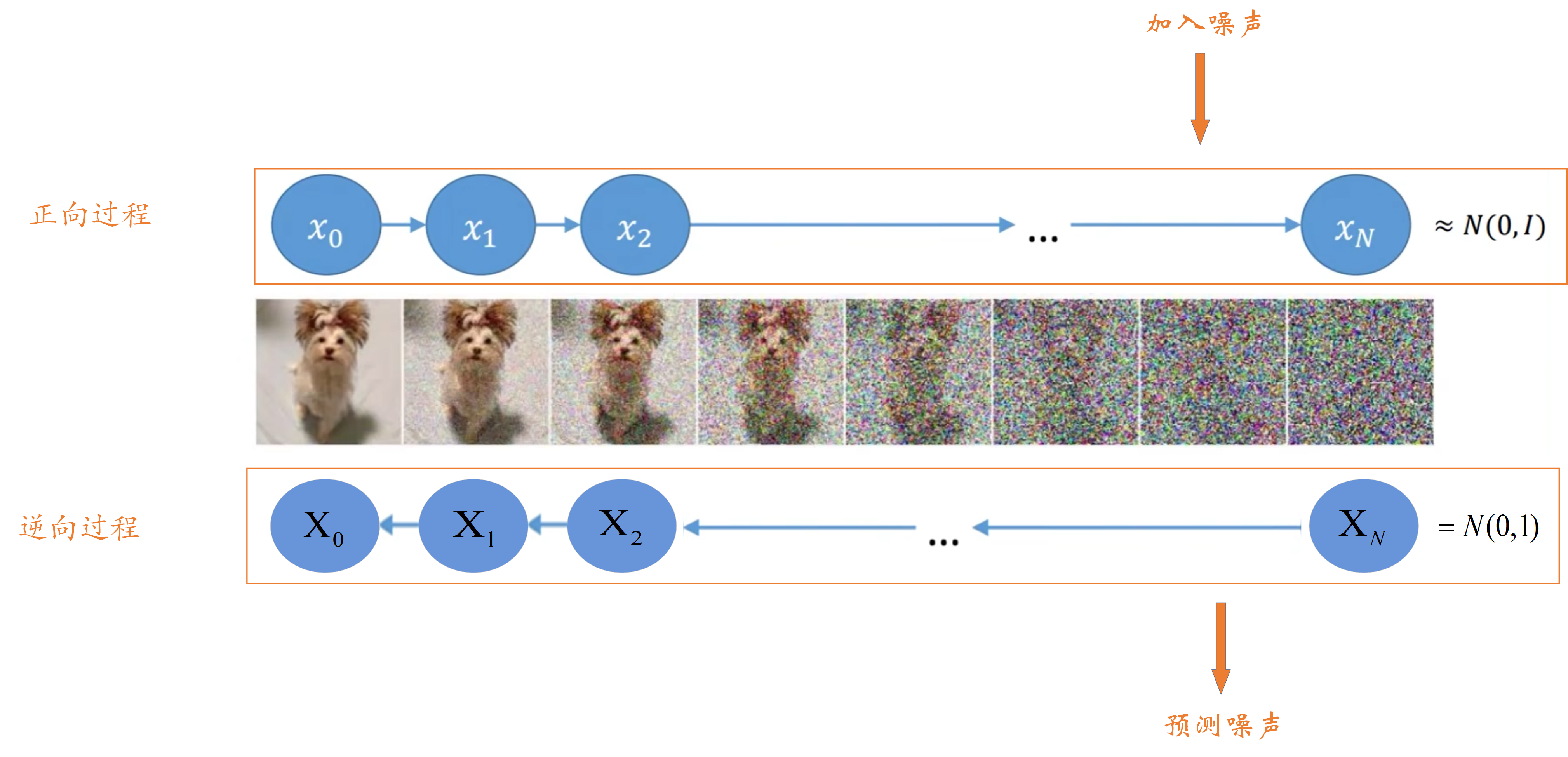
  我们在正向过程中加入的噪声其实都是已知的，是可以作为真实值的。而逆向过程相当于一个去噪过程，我们用一个模型来预测噪声，让正向过程每一步加入的噪声和逆向过程对应步骤预测的噪声尽可能一致，而逆向过程预测噪声的方式就是丢入模型训练，其实就是Training中的第五步。

• Sampling

  知道了训练过程，采样过程就很简单了，其实采样过程就对应我们理论部分介绍的逆向过程，由一个高斯噪声一步步向前迭代，最终得到$X_0$时刻图像。

 

代码解析

  首先，按照我们理论部分应该有一个正向过程，其最重要的就是最后得出的公式7，如下：

​ $X_t=\sqrt{{\bar{a}}_t}{X}_0+\sqrt{1-{\bar{a}}_t}{\hat{Z}}_t$

  那么我们在代码中看一看是如何利用这个公式7的，代码如下：

def noise_images(self, x, t):
    sqrt_alpha_hat = torch.sqrt(self.alpha_hat[t])[:, None, None, None]
    sqrt_one_minus_alpha_hat = torch.sqrt(1 - self.alpha_hat[t])[:, None, None, None]
    Ɛ = torch.randn_like(x)
    return sqrt_alpha_hat * x + sqrt_one_minus_alpha_hat * Ɛ, Ɛ

  Ɛ为随机的标准高斯分布，其实也就是真实值。大家可以看出，上式的返回值sqrt_alpha_hat * x + sqrt_one_minus_alpha_hat其实就表示公式7。【注：这个代码我省略了很多细节，我只把关键的代码展示给大家看，要想完全明白，还需要大家记住调试调试了】

  接着我们就通过一个模型预测噪声，如下：

predicted_noise = model(x_t, t)

  model的结构很简单，就是一个Unet结构，然后里面嵌套了几个Transformer机制，我就不带大家跳进去慢慢看了。现在有了预测值，也有了真实值Ɛ【返回后Ɛ用noise表示】，就可以计算他们的损失并不断迭代了。

loss = mse(noise, predicted_noise)
optimizer.zero_grad()
loss.backward()
optimizer.step()

---

  上述其实就是训练过程的大体结构，我省略了很多，要是大家有任何问题的话可以评论区留言讨论。现在就来看看采样过程的代码吧！！！

def sample(self, model, n):
    logging.info(f"Sampling {n} new images....")
    model.eval()
    with torch.no_grad():
        x = torch.randn((n, 3, self.img_size, self.img_size)).to(self.device)
        # for i in tqdm(reversed(range(1, self.noise_steps)), position=0):
        for i in tqdm(reversed(range(1, 5)), position=0):
            t = (torch.ones(n) * i).long().to(self.device)
            predicted_noise = model(x, t)
            alpha = self.alpha[t][:, None, None, None]
            alpha_hat = self.alpha_hat[t][:, None, None, None]
            beta = self.beta[t][:, None, None, None]
            if i > 1:
                noise = torch.randn_like(x)
            else:
                noise = torch.zeros_like(x)
            x = 1 / torch.sqrt(alpha) * (x - ((1 - alpha) / (torch.sqrt(1 - alpha_hat))) * predicted_noise) + torch.sqrt(beta) * noise   
    model.train()
    x = (x.clamp(-1, 1) + 1) / 2
    x = (x * 255).type(torch.uint8)
    return x

  上述代码关键的就是 x = 1 / torch.sqrt(alpha) * (x - ((1 - alpha) / (torch.sqrt(1 - alpha_hat))) * predicted_noise) + torch.sqrt(beta) * noise这个公式，其对应着代码流程图中Sampling阶段中的第4步。需要注意一下这里的跟方差${\sigma }_t$这个公式给的是$\sqrt{\beta }$，但其实在我们理论计算时为$\sqrt{\frac{{\beta }_t(1-{\bar{a}}_{t-1})}{1-{\bar{a}}_t}}$，这里做了近似处理计算，即${\bar{a}}_{t-1}$和${\bar{a}}_t$都是非常小且近似0的数，故把$\frac{(1-{\bar{a}}_{t-1})}{1-{\bar{a}}_t}$当成1计算，这里注意一下就好。🍵🍵🍵

 

代码小结

  可以看出，这一部分我所用的篇幅很少，只列出了关键的部分，很多细节需要大家自己感悟。比如代码中时刻T的用法，其实是较难理解的，代码中将其作为正余弦位置编码处理。如果你对位置编码不熟悉，可以看一下我的这篇文章的附录部分，有详细的介绍位置编码，相信你读后会有所收获。🌿🌿🌿

 

参考链接

由浅入深了解Diffusion🍁🍁🍁

 

附录

高斯分布性质

高斯分布又称正态分布，其表达式为：

​ $$f(x)=\frac{1}{\sqrt{2\pi \sigma }}{e}^{-\frac{{(x-u)}^2}{2{\sigma }^2}}$$

其中$u$为均值，${\sigma }^2$为方差。若随机变量服X从正态均值为$u$，方差为${\sigma }^2$的高斯分布，一般记为$X\sim N(u,{\sigma }^2)$。此外，有一点大家需要知道，如果我们知道一个随机变量服从高斯分布，且知道他们的均值和方差，那么我们就能写出该随机变量的表达式。

---

高斯分布还有一些非常好的性质，现举一些例子帮助大家理解。

• 若$X\sim N(u,{\sigma }^2)$，则$aX\sim N(au,(a\sigma {)}^2)$。
• 若$X\sim N(u_1,{{\sigma }^2}_1)$，$Y\sim N(u_2,{{\sigma }^2}_2)$，则$X+Y\sim N(u_1+u_2,{{\sigma }^2}_1+{{\sigma }^2}_2)$。

 
 
如若文章对你有所帮助，那就🛴🛴🛴