10.1 图的基本概念(P214)
10.2 图的存储(P215)
10.3 图的遍历和连通性(P217)
bfs 和 dfs 。
10.4 拓扑排序(P219)
一个图能进行拓扑排序的充要条件是它是一个有向无环图。
算法思想
这里使用 bfs 求拓扑排序,基本步骤为:
- 所有入度为
0的结点入队。 - 弹出队首元素
u,遍历所有从u出发的边,将这些边的终点的入度减一,然后判断其入度是否为0,如果是则将该点入队。 - 继续上述操作,直到队列为空。若所有结点都曾经进出队,则图的拓扑排序找到,结点出队顺序即为一个拓扑序;如果某些结点没有入队,则说明该图的拓扑排序不存在。
似乎可以使用拓扑排序来判断一个图是否为 DAG ?
时间复杂度为 O ( V + E ) O(V+E) O(V+E) 。
特别地,如果题目要求输出字典序最小的拓扑序,则可以考虑使用上述算法中的队列换成优先队列。
例1 HDU 1285 确定比赛名次
题目大意
有 n n n 支队伍,有 m m m 个胜负关系,输出字典序最小的队伍排序。
思路
拓扑排序模板题,由于题目要求输出字典序最小的排序,所以需要使用单调队列。
代码(部分)
// 小根堆
priority_queue< int, vector<int>, greater<int> > q;
void bfs(){
for(int i=1;i<=n;i++){
if(!in[i]){
q.push(i);
}
}
while(!q.empty()){
int cur = q.top();
if(first) first = 0;
else cout<<' ';
cout<<cur;
q.pop();
for(int i=head[cur];i!=0;i=edge[i].next){
int to = edge[i].to;
in[to]--;
if(!in[to]) q.push(to);
}
}
return;
}
例2 POJ 1270 Following Orders
题目大意
给定 n ≤ 30 n\leq30 n≤30 个元素和 m ≤ 50 m\leq50 m≤50 个约束关系 x i < y i x_i<y_i xi<yi,按照字典序输出所有满足约束关系的元素序列。
思路
由于本题需要输出所有的拓扑序,所以最好使用 dfs 来实现拓扑排序,具体实现见代码。
代码(部分)
void topu(int x, int d){
ans[d] = x;
vis[x] = 1;
if(d == cnt){
for(int i=1;i<=cnt;i++){
cout<<(char)(ans[i]-1+'a');
}
cout<<'\n';
return;
}
for(int i=head[x];i!=0;i=edge[i].next){
int to = edge[i].to;
in[to]--;
}
for(int i=1;i<=cnt;i++){
if(in[a[i]]==0 && !vis[a[i]]){
topu(a[i], d+1);
}
}
for(int i=head[x];i!=0;i=edge[i].next){
int to = edge[i].to;
in[to]++;
}
vis[x] = 0;
}
例3 HDU 4857 逃生
题目大意
输出这样的拓扑序:1 号尽量靠前,然后让 2 号尽量靠前,以此类推。
思路
参考:https://blog.csdn.net/AC__dream/article/details/120235928
在刚拿到这个题的时候,我误认为输出字典序最小的拓扑序即可,但其实题目要求的并不是这样。
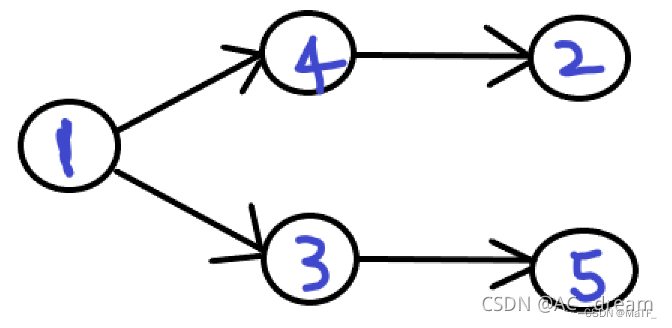
从上图的例子我们可以看出,如果字典序最小的拓扑序是:1, 3, 4, 2, 5 ,而真正的答案是:1, 4, 2, 3, 5 ,因为后者 2 的位置前者更靠前。我们注意到这样一个事实:如果 1 到 i-1 的位置固定,i 的位置越靠前,则该序列的逆序列的字典序越大 。
所以,我们可以建反图,然后得到反图中字典序最大的拓扑序,最后反着输出即可。
本题的输入会有重边的现象,但不会造成影响。
代码(部分)
priority_queue< int, vector<int>, less<int> > q;
void topu(){
for(int i=1;i<=n;i++){
if(in[i] == 0){
q.push(i);
}
}
while(!q.empty()){
int cur = q.top();
q.pop();
s.push(cur);
for(int i=head[cur];i!=0;i=edge[i].next){
int to = edge[i].to;
in[to]--;
if(in[to] == 0){
q.push(to);
}
}
}
}
例4 HDU 1811 Rank of Tetris
题目大意
给定 n < 10000 n<10000 n<10000 个选手,给定 m < 20000 m<20000 m<20000 个形如: A > B A>B A>B 、 A = B A=B A=B 、 A < B A<B A<B 的约束条件,表示 A、B 两个选手之间的得分关系。规定:如果两个选手得分相同,则序号大者排名高。问:根据这些约束条件能否唯一确定一个排名?是否存在冲突?
思路
相等关系用并查集维护,不等关系则对应一条有向边;先处理所有相等关系,再处理不等关系。进行拓扑排序时,如果某一时刻同时存在两个及以上结点的入度为 0 0 0 ,说明排名不确定;如果有些结点从未被访问过,则说明存在冲突。
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e4+5;
const int maxm = 2e4+5;
int n, m;
int f[maxn], siz[maxn];
int head[maxn];
int in[maxn];
int tot = 0;
set<int> s;
bool uncertain = 0, conflict = 0;
int sum = 0;
struct NODE{
int u, v;
char c;
};
NODE node[maxm];
struct EDGE{
int to;
int next;
};
EDGE edge[maxm];
void addEdge(int fr, int to){
tot++;
edge[tot].to = to;
edge[tot].next = head[fr];
head[fr] = tot;
in[to]++;
}
void init(){
uncertain = conflict = 0;
s.clear();
sum = tot = 0;
memset(head, 0, sizeof(head));
memset(in, 0, sizeof(in));
for(int i=0;i<n;i++){
f[i] = i;
siz[i] = 1;
}
}
int find(int x){
return x == f[x] ? x : f[x]=(find(f[x]));
}
void merge(int x, int y){
if(siz[x] < siz[y]){
f[x] = y;
siz[y] += siz[x];
}
else{
f[y] = x;
siz[x] += siz[y];
}
}
void topu(){
int cnt = 0;
for(int i=0;i<n;i++){
int x = find(i);
if(i==x && in[x]==0){
s.insert(x);
}
}
while(!s.empty()){
if(s.size() > 1){
uncertain = 1;
}
int cur = *s.begin();
cur = find(cur);
s.erase(s.begin());
cnt++;
for(int i=head[cur];i!=0;i=edge[i].next){
int to = edge[i].to;
to = find(to);
in[to]--;
if(in[to] == 0){
s.insert(to);
}
}
}
if(cnt != sum){
conflict = 1;
}
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
while(cin>>n>>m){
init();
for(int i=1;i<=m;i++){
cin>>node[i].u>>node[i].c>>node[i].v;
}
for(int i=1;i<=m;i++){
int x = find(node[i].u), y = find(node[i].v);
if(node[i].c == '='){
if(x == y) continue;
else merge(x, y);
}
}
for(int i=1;i<=m;i++){
int x = find(node[i].u), y = find(node[i].v);
if(node[i].c == '<'){
addEdge(y, x);
}
else if(node[i].c == '>'){
addEdge(x, y);
}
}
for(int i=0;i<n;i++){
if(i == find(i)){
sum++;
}
}
topu();
if(conflict) cout<<"CONFLICT\n";
else if(uncertain) cout<<"UNCERTAIN\n";
else cout<<"OK\n";
}
return 0;
}
10.5 欧拉路和欧拉回路(P223)
欧拉路和欧拉回路是否存在
- 无向图:如果所有结点的度均为偶数,则存在欧拉回路,任意结点均可以作为起点;如果有且仅有两个结点的度为奇数,则存在欧拉路,两个奇数点分别作为起点和终点。
- 有向图:定义有向图中,结点的度为出度与入度之差。如果所有结点的度均为 0 0 0 ,则存在欧拉回路;如果只有一个结点的度为 1 1 1 ,一个结点的度为 − 1 -1 −1 ,其余结点的度均为 0 0 0 ,则存在欧拉路。
输出一个欧拉回路
例子见 P224 。
void dfs(int x){
for(int i=1;i<=maxc;i++){
if(dis[x][i]){
// 这条边已经走过,之后不能再走
dis[x][i]--, dis[i][x]--;
dfs(i);
cout<<i<<" "<<x<<"\n";
}
}
}
如果欧拉回路过长,则 dfs 很有可能出现“爆栈”的情况,这时候就需要使用非递归的 dfs 算法。非递归 dfs 实现简单地说就是把 不同bfs 的队列换成栈。
10.6 无向图的连通性(P225)
10.6.1 割点和割边(P225)
在一个无向图中,能够相互连通的结点构成一个连通块,如果删除连通块中的某个结点,会导致其他结点不再相互连通,则这个点称为割点。具有相似性质的边称为割边。
我们用下面两条定理引出求割点的 tarjan 算法:
- 对于一颗 dfs 生成树 T T T 的根节点 s s s , s s s 是割点当且仅当 s s s 有两个及以上的子结点。
- 对于一颗 dfs 生成树 T T T 的非根节点 u u u , u u u 是割点当且仅当 u u u 存在某一个子结点 v v v , v v v 及其后代都没有回退边连回 u u u 的祖先。
例1 P3388 【模板】割点(割顶)
题目大意
给定一个无向图,输出割点个数和所有割点的编号。
思路
tarjan 求割点模板题。
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn = 2e4+5;
const int maxm = 1e5+5;
int n, m;
int head[maxn];
int tot = 0;
int idx = 0;
int dfn[maxn], low[maxn];
int cnt = 0;
int ans[maxn];
bool isCut[maxn];
struct EDGE{
int to;
int next;
};
EDGE edge[maxm<<1];
void addEdge(int fr, int to){
tot++;
edge[tot].to = to;
edge[tot].next = head[fr];
head[fr] = tot;
}
void tarjan(int x, int fa){
idx++;
int child = 0;
dfn[x] = low[x] = idx;
for(int i=head[x];i!=0;i=edge[i].next){
int to = edge[i].to;
if(to == fa) continue;
if(!dfn[to]){
child++;
tarjan(to, x);
low[x] = min(low[x], low[to]);
if(low[to]>=dfn[x] && x!=fa){
isCut[x] = 1;
}
}
else{
low[x] = min(low[x], dfn[to]);
}
}
if(x==fa && child>=2){
isCut[x] = 1;
}
if(isCut[x]) cnt++;
}
void solve(){
for(int i=1;i<=n;i++){
if(!dfn[i]){
// 当且仅当x为根节点时,有x==fa
tarjan(i, i);
}
}
cout<<cnt<<'\n';
for(int i=1;i<=n;i++){
if(isCut[i]) cout<<i<<' ';
}
return;
}
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
int u, v;
cin>>u>>v;
addEdge(u, v);
addEdge(v, u);
}
solve();
return 0;
}