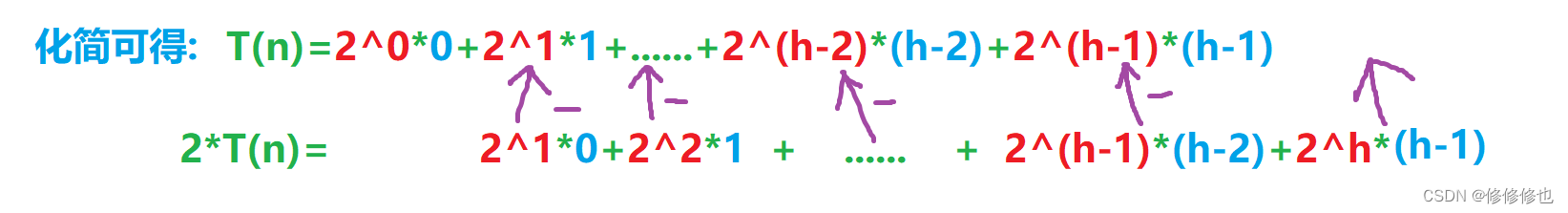【数据结构】什么是堆?

news2024/9/30 11:33:38

🦄个人主页:修修修也

🎏所属专栏:数据结构

⚙️操作环境:Visual Studio 2022

堆的概念及结构

堆的定义如下:

n个元素的序列{k1,k2,...,kn}当且仅当满足以下关系时,称之为堆.

$\left\{\begin{matrix} k_{i}\geqslant k_{2i} \\ k_{i}\geqslant k_{2i+1} & & \end{matrix}\right.$ 或 $\left\{\begin{matrix} k_{i}\leqslant k_{2i} \\ k_{i}\leqslant k_{2i+1} & & \end{matrix}\right.$

$(i= 1,2,...,\left \lfloor \frac{n}{2} \right \rfloor)$

把这个序列对应的一维数组(即以一维数组作此序列的存储结构)看成是一个完全二叉树,则堆的含义表明,完全二叉树中所有双亲结点的值均不小于(或不大于)其左,右孩子结点的值.

由此,若序列 {k1,k2,...,kn}是堆,则堆顶元素(或完全二叉树的根)必为序列中n个元素的最大值(或最小值).

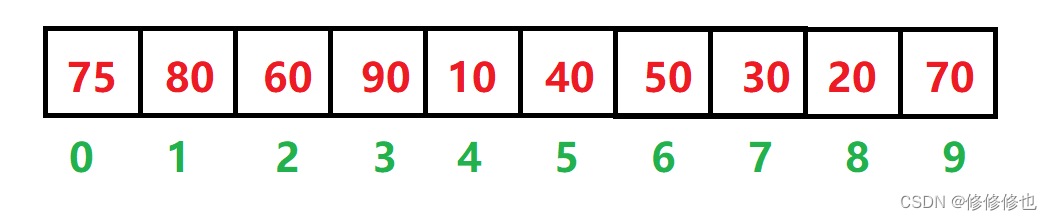
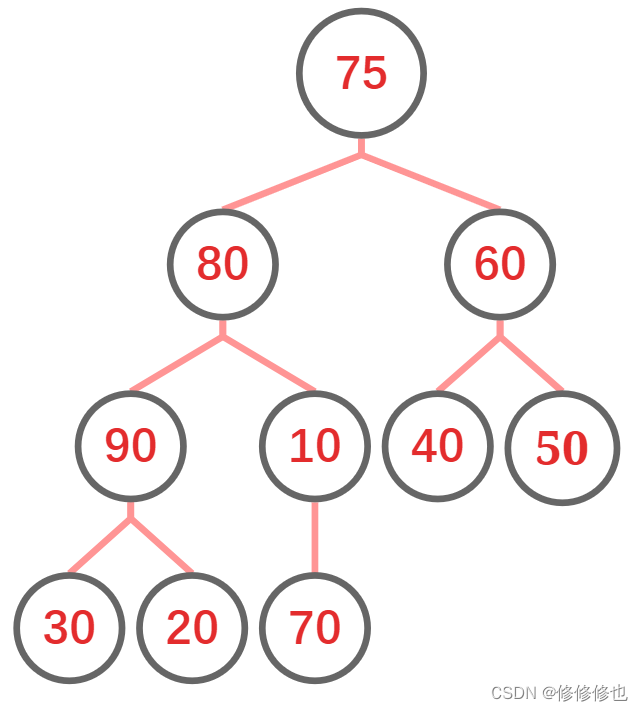
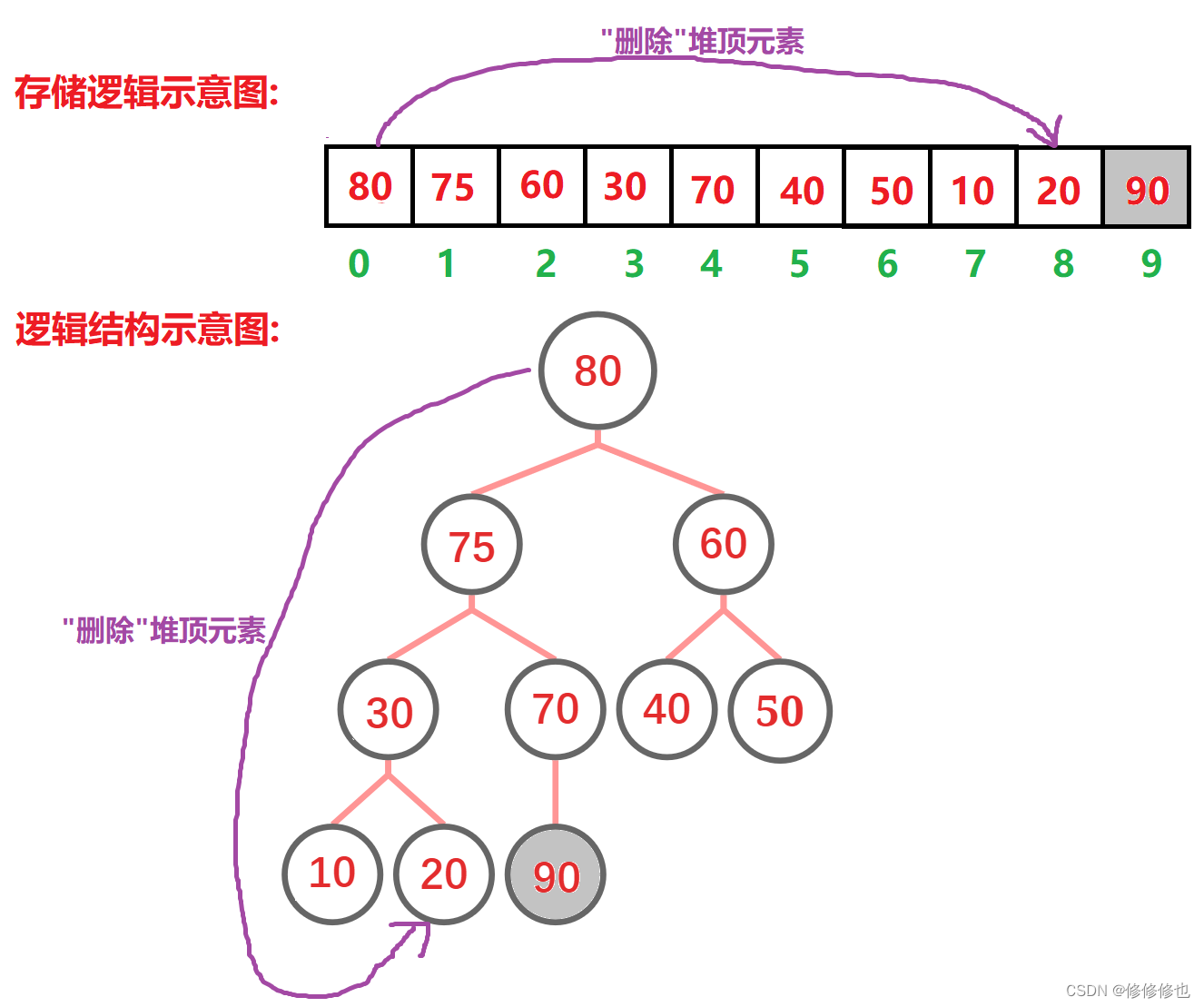
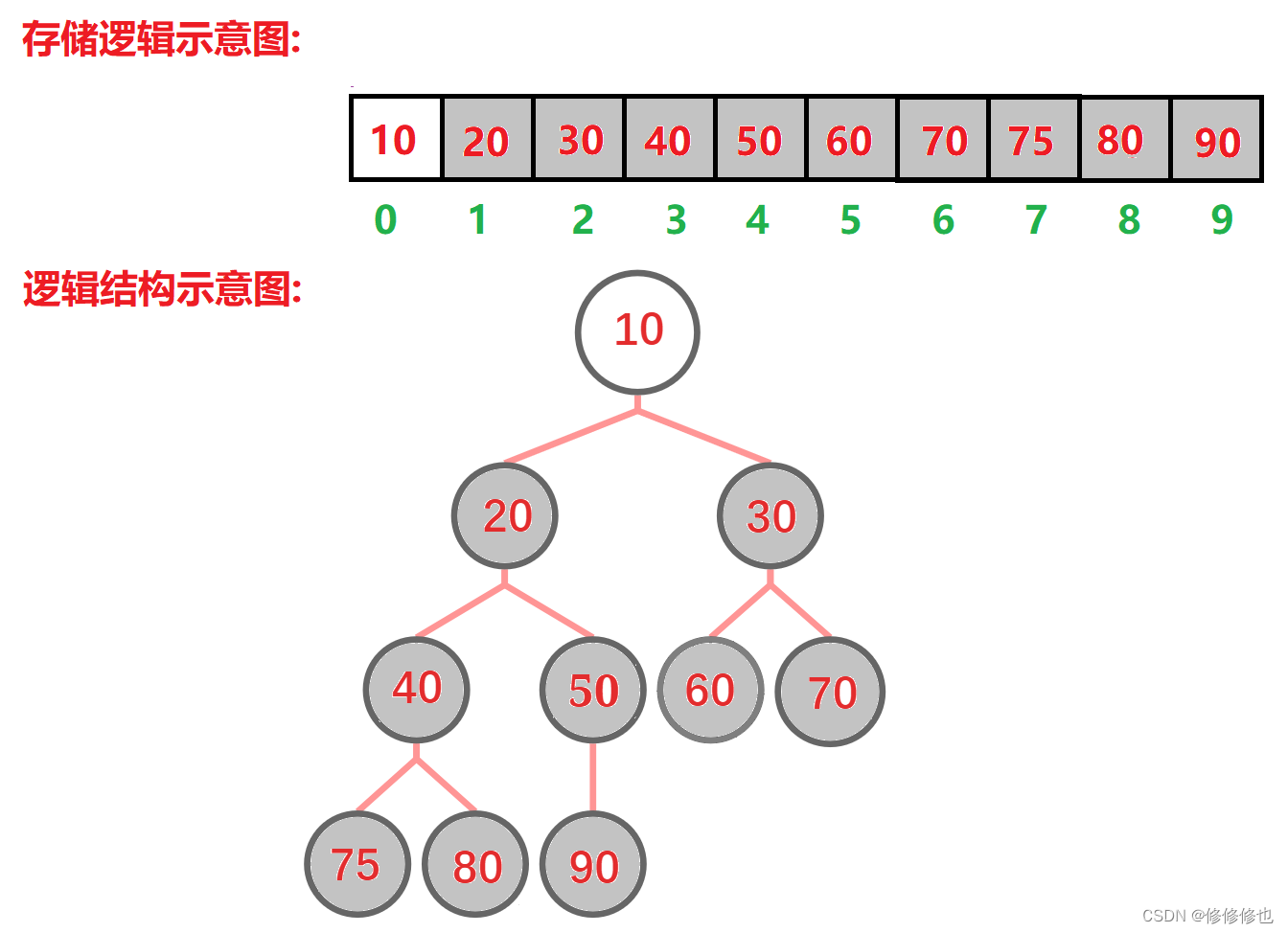
如下面两个序列为堆(存储结构),则其对应的完全二叉树(逻辑结构)如下图所示:

综上,我们不难总结出堆的性质:

堆中某个结点的值总是不大于或不小于其父亲结点的值.
堆总是一颗完全二叉树.

堆的实现

有关堆结构的完整实现部分我放在下面这篇博客中为大家详细梳理了,并且为每个算法逻辑配备了详细明了的逻辑结构演示图和物理结构演示图,如:

对堆的实现部分的具体逻辑和细节感兴趣的朋友可以点击下方链接直接跳转到相应文章:

【数据结构】C语言实现堆(附完整运行代码)http://t.csdnimg.cn/v7qVo

建堆的时间复杂度

建堆有两种方式,一种是从堆顶开始向下建堆,另一种是从堆尾开始向上建堆.乍一听好像两种建堆方式除了向上调整和向下调整方式不同之外没什么区别,但我们仔细分析一下,其实这两种建堆方式的时间复杂度差别是很大的.

向上调整建堆

我们先一起来分析一下向上建堆的时间复杂度:

首先,按照算法算法最坏时间复杂度分析,我们假设堆是完全二叉树中的满二叉树,并且假设每个结点的移动次数都是最坏移动次数,则:

使用错位相消法,可得:

化简,可得:

使用大O阶渐近表示法,可得:

$T(n) = 2^h*h = O(n*log_{2}n)$

因为:

$2^h=n$

$h=log_{2}n$

(舍去低次方阶和常数阶后剩下的2^h恰好是高为h的树的结点个数n,同样的h也可化简为以2为底n的对数)

向下调整建堆

再来看看向下调整建堆:

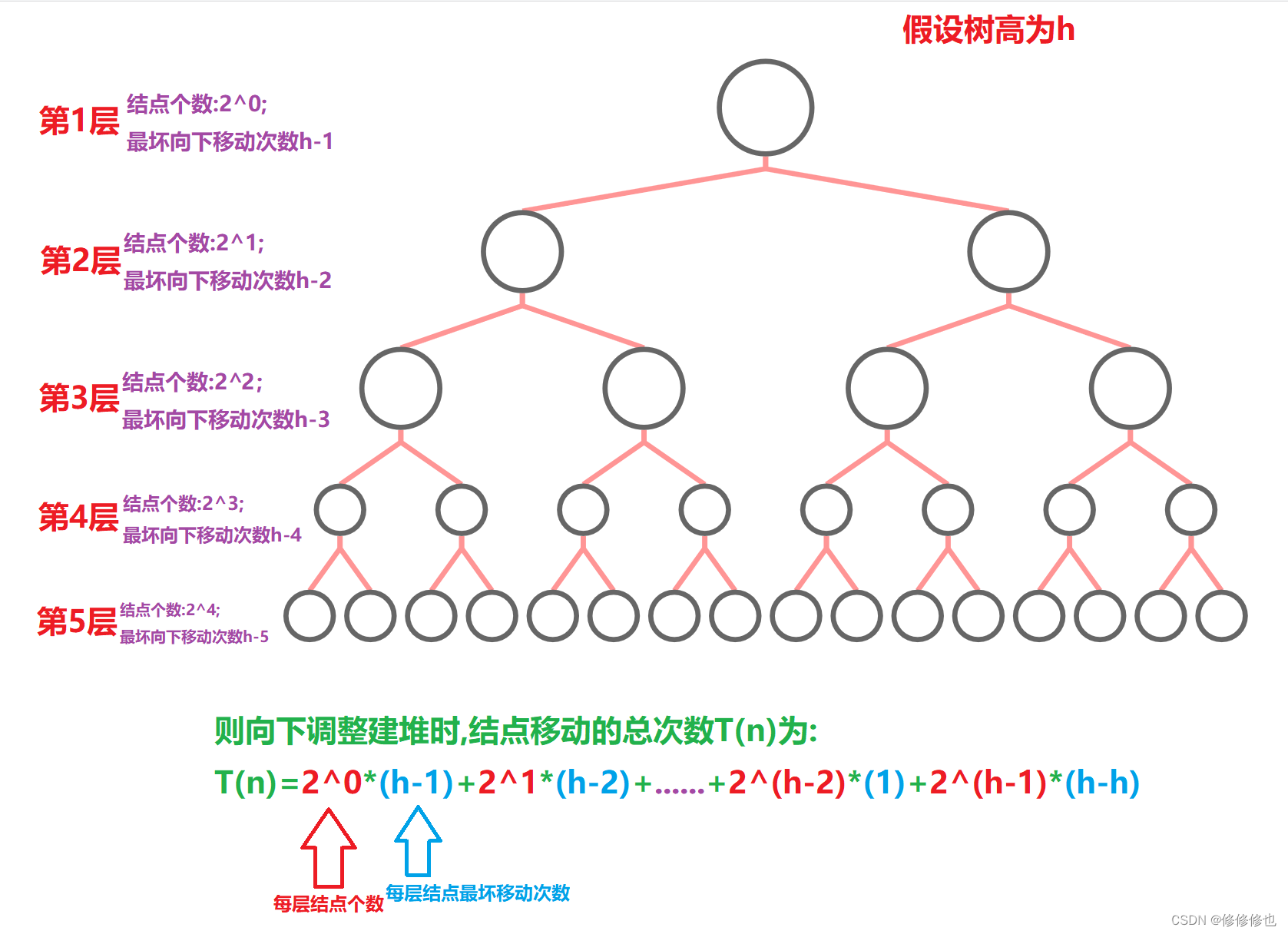
我们继续,按照算法最坏时间复杂度分析,假设堆是完全二叉树中的满二叉树,并且假设每个结点的移动次数都是最坏移动次数,则:

使用错位相消法,可得T(n)为:

化简,可得:

使用大O阶渐近表示法,可得:

T(n) = 2^h = O(n)

(舍去低次方阶和常数阶后剩下的2^h恰好是高为h的树的结点个数n)

综上可知:

向上调整的建堆方式的时间复杂度为 $O(n*log_{2}n)$
向下调整的建堆方式的时间复杂度为 $O(n)$
向下调整建堆是优于向上调整建堆的.

堆思想的应用

1.堆排序

堆排序就是利用堆(假设利用大堆)进行排序(假设为升序)的算法.

它的基本思想是:

将待排序的序列构造成一个大堆.

此时,整个序列的最大值就是堆顶的根结点.将它移走(其实就是我们前面堆实现中的出堆顶操作).

然后将剩余的n-1个序列重新构造成一个堆,这样就会得到n个元素中的次小值(即堆顶).

如此反复执行,就可以得到一个有序的序列了.

使用堆排序的思想排序有以下几点需要注意的:

排升序建大堆
排降序建小堆
建好堆后利用堆删除的思想进行排序

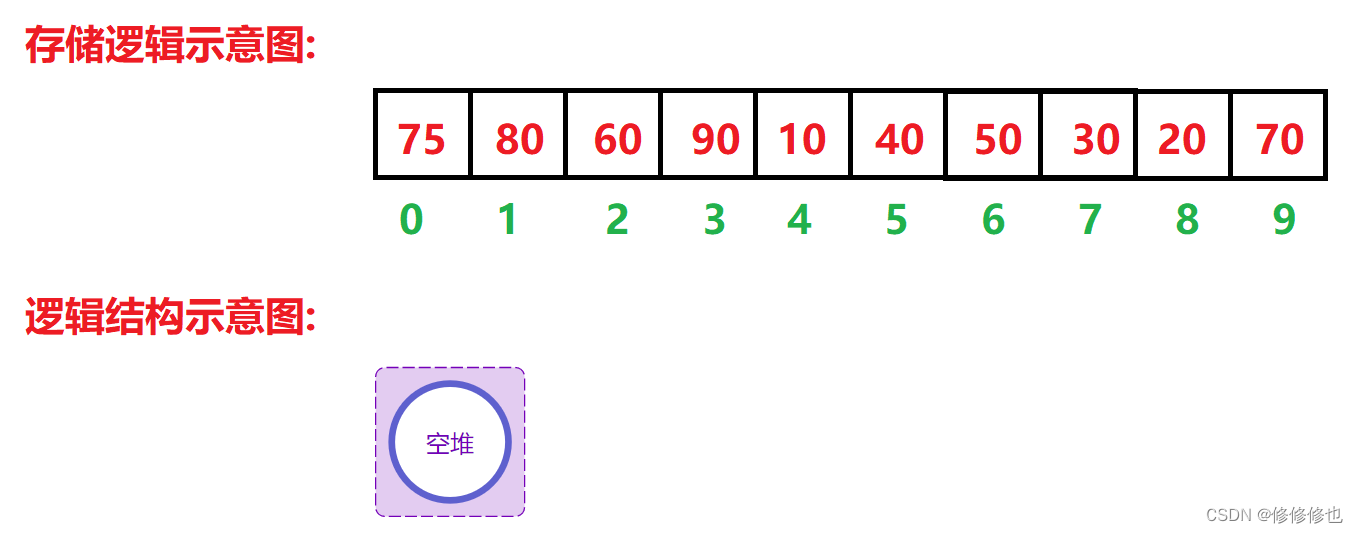
如下是一个顺序待排数组:

为了直观的利用堆排序的思想,我们在逻辑上将其还原为一颗完全二叉树:

我们先将数组视为一个空堆,开始时堆中没有元素.

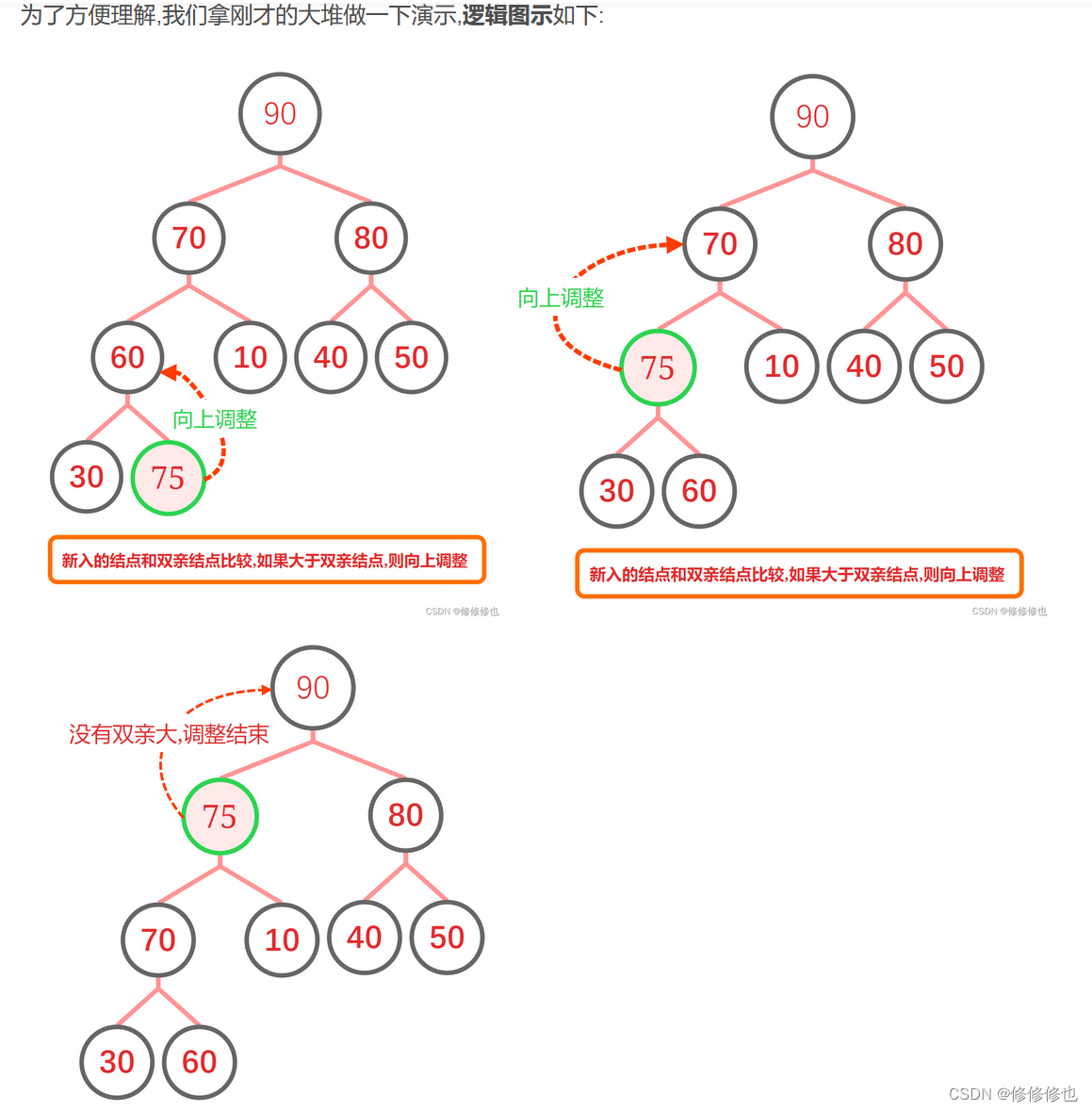
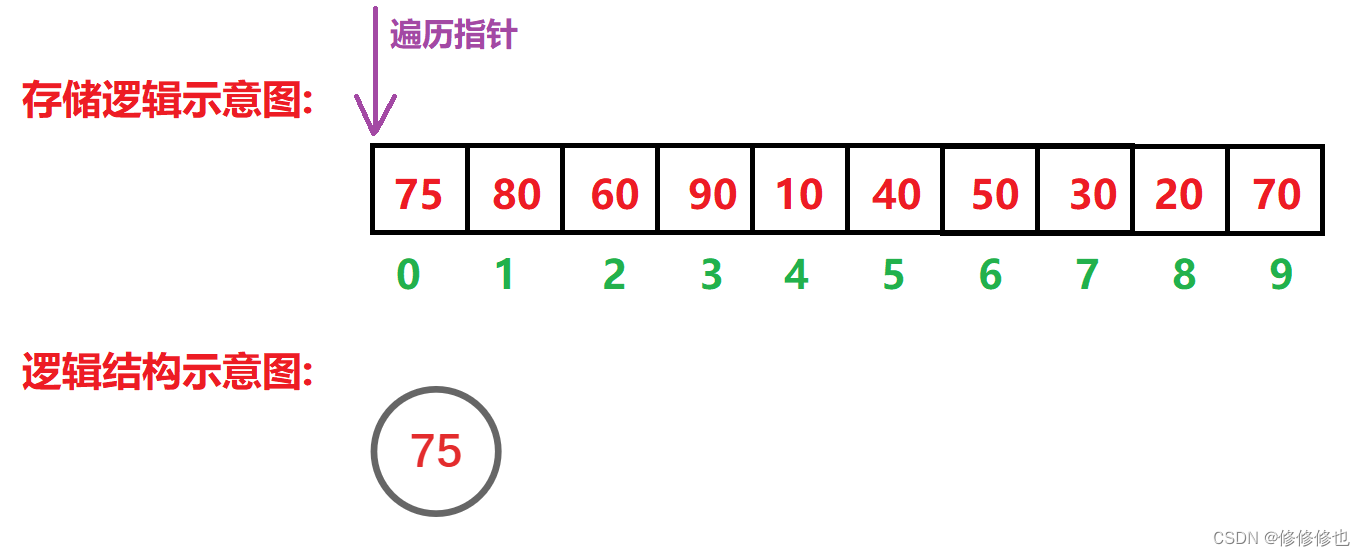
我们先模拟一下向上建堆的过程:

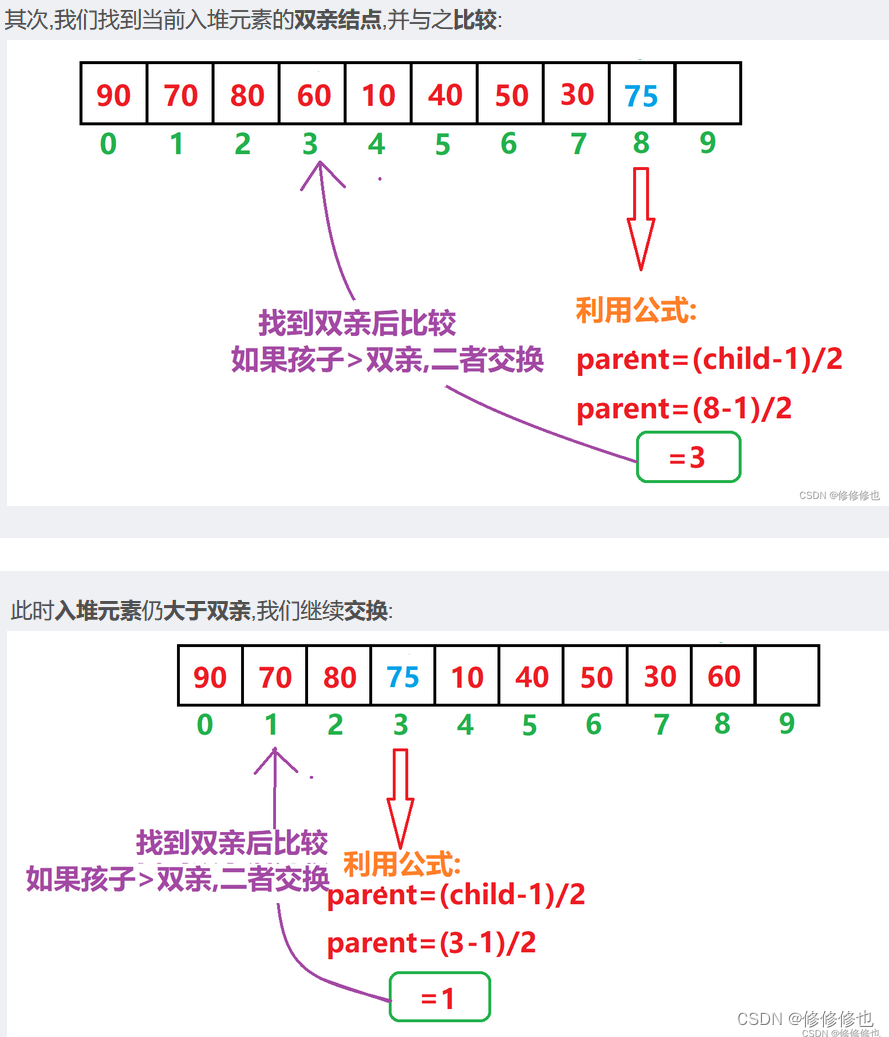
即数组逐渐向后遍历,模拟向堆中插入元素:

(ps:此处建堆也可以使用向下建堆的思路,时间复杂度会更小,但要注意的是,向下建堆时,我们对数组的遍历是从最后一个叶子结点的父节点开始向前遍历并向下调整的.假设数组有n个元素,即是从下标为[(n-2)/2]的结点开始向前遍历并向下调整.)

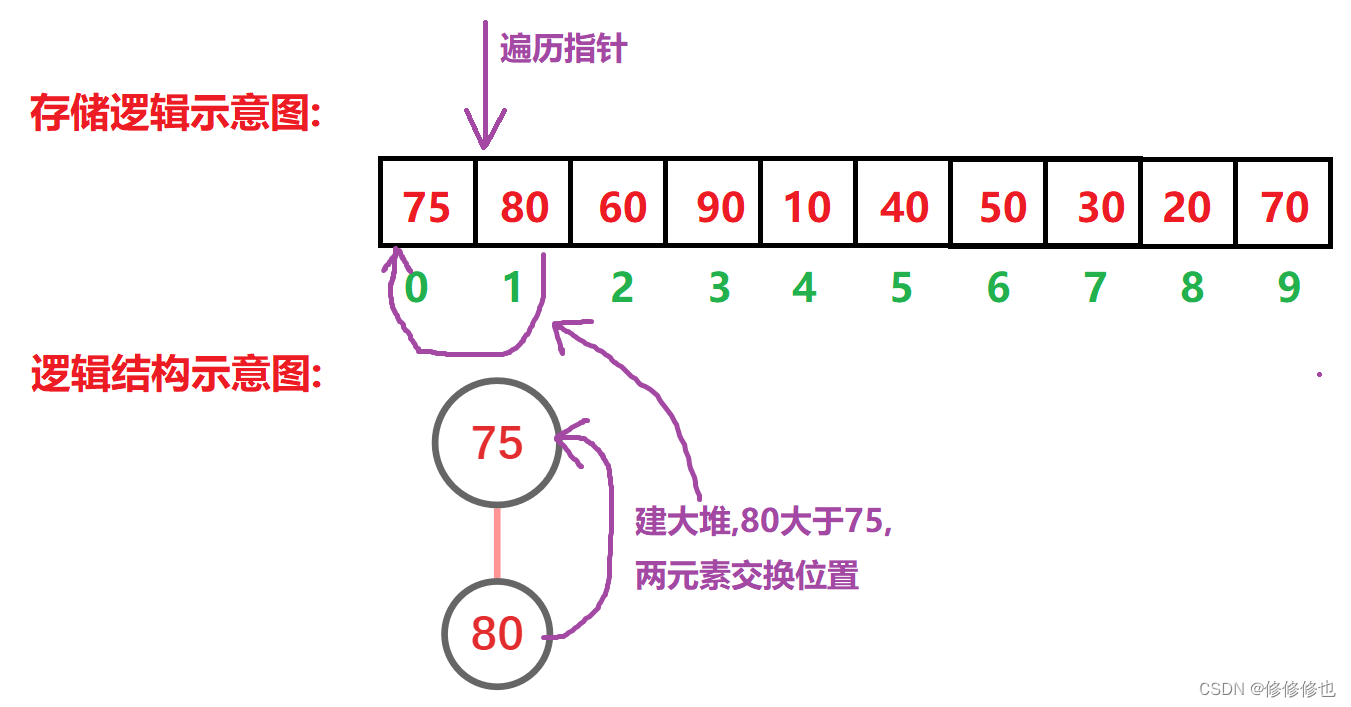
插入'75':

插入'80':

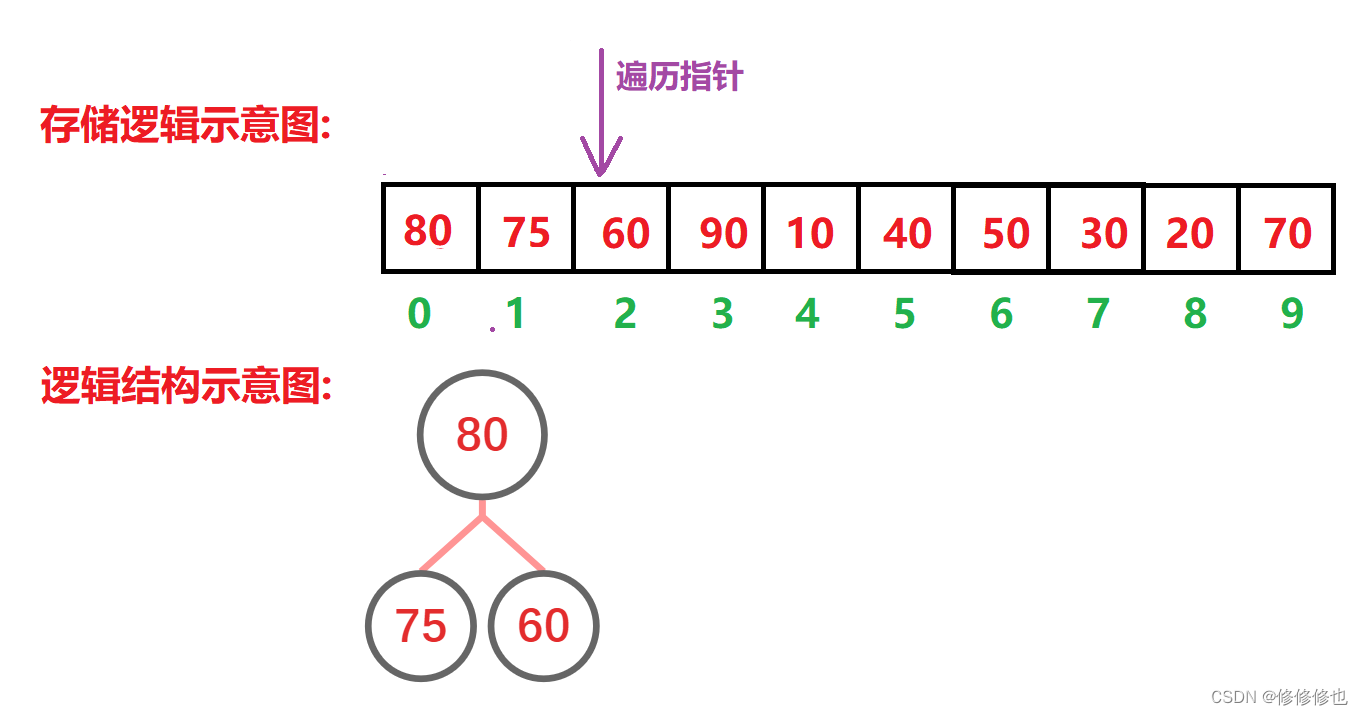
向上调整:

插入'60':

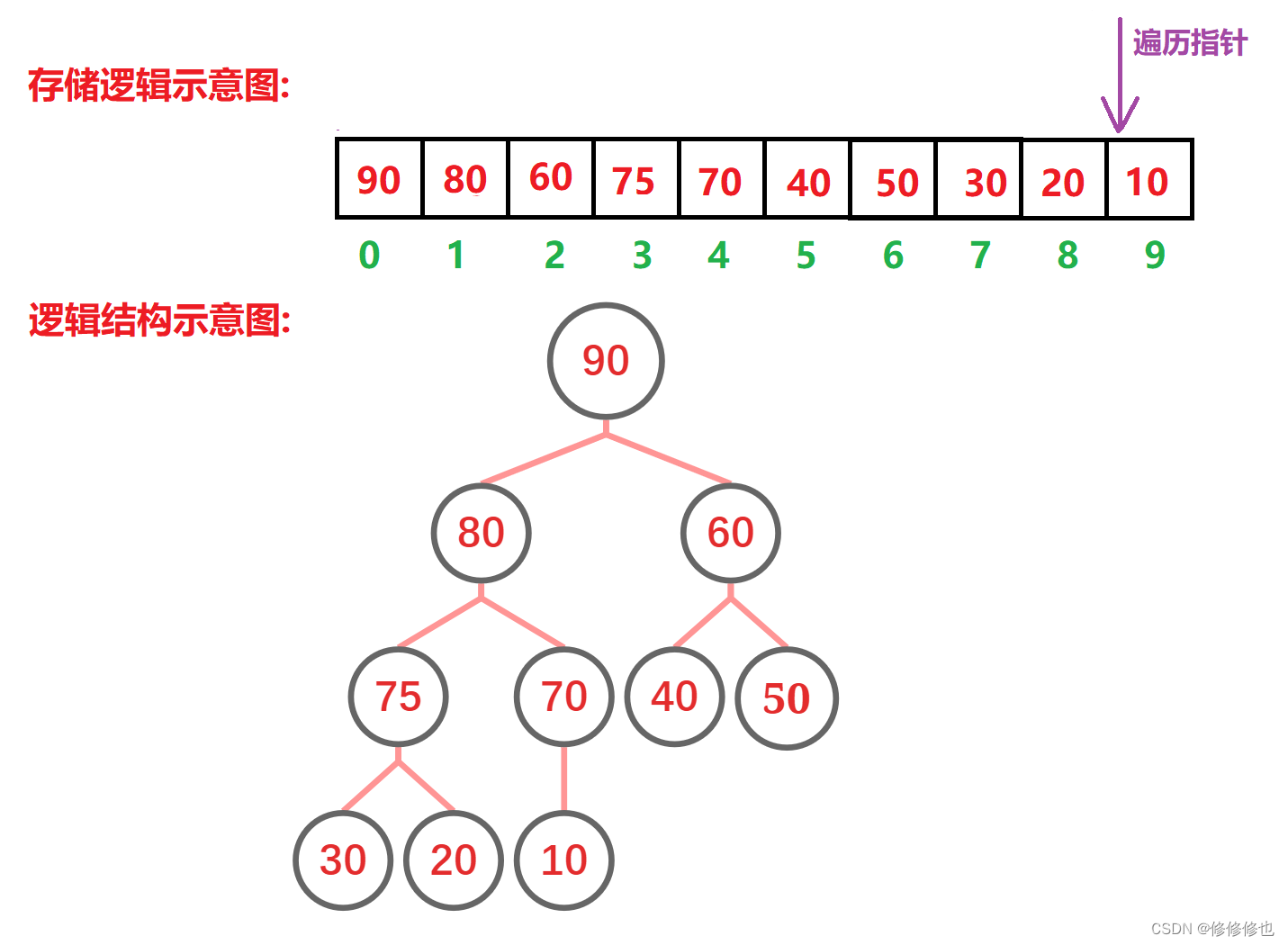
我们先按照入堆的逻辑,将数组建成一个大堆:

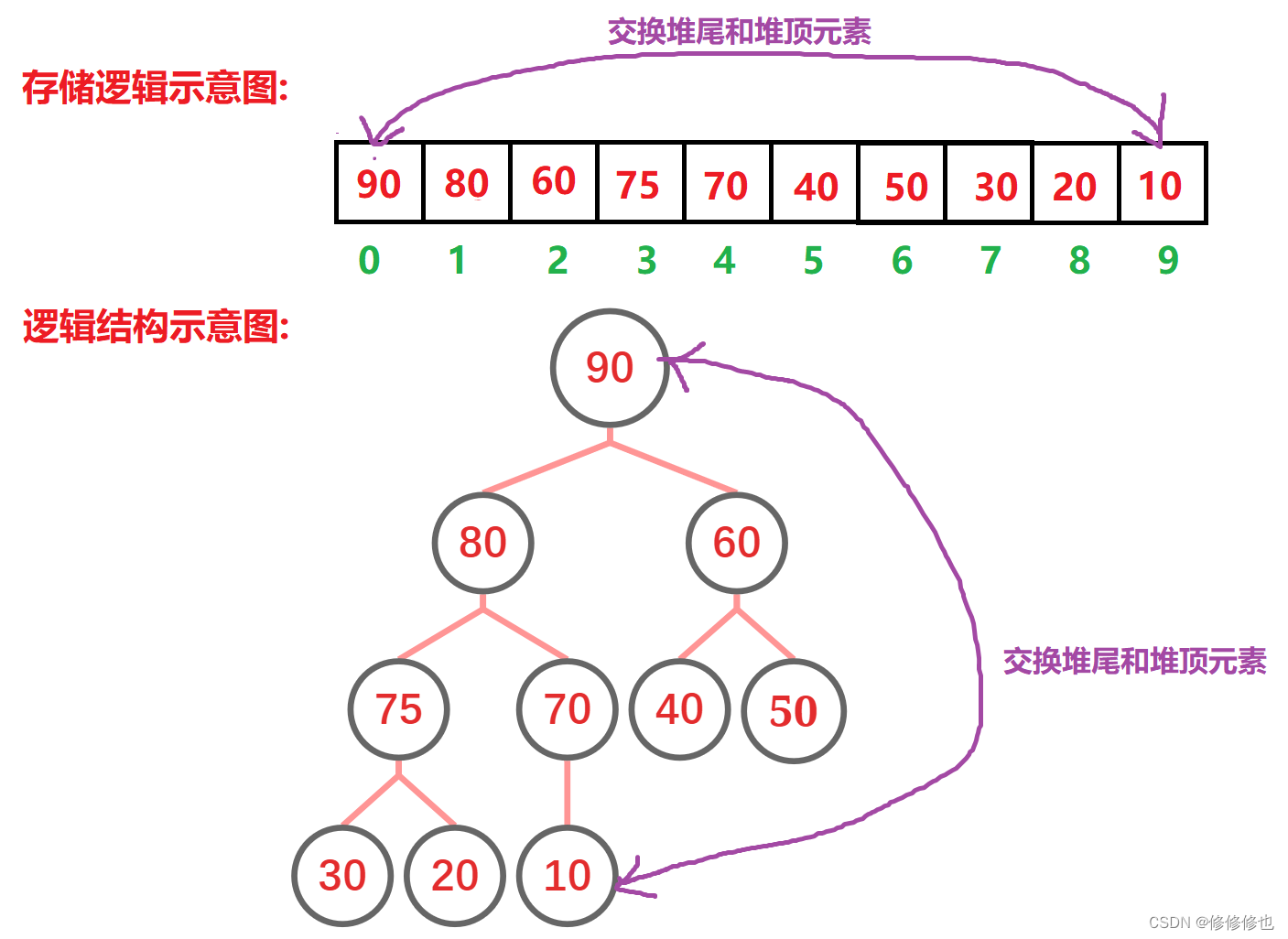
然后再按照堆删除的思想,将堆顶元素移动至堆尾"删除":

再将换到堆顶的元素向下调整:

调整好后再删除"新的堆顶元素":

如此循环"删除堆顶":

最终就会得到一个升序的序列:

2.Top-k问题

Top-k问题:

即求数据集合中前k个最大/最小的元素,一般情况下数据量都比较大.

对于Top-k问题,最容易想到的方法是先整体排序,再取前k个,但当数据量非常大时(可能都无法加载到内存上),排序就不是一个很好的解决方法了.

这时的最佳的方案就是用堆来解决,思路如下:

1.先用数据元素中前K个元素来建堆

求前k个最大的元素,则建小堆
求前k个最小的元素,则建大堆

2.遍历剩余的N-K个元素来比较,遇到符合条件的(如求前k个最大的元素,新元素比堆顶要大)则用其替换堆顶,然后再向下调整,构建为新的大堆/小堆.

3.当遍历完剩下N-K个元素时,堆中剩余的k个元素就是所求的前Top-k个元素.

这个思路有点类似于让一个堆里最"弱"的元素去守"门",如果新来的元素比最弱的强,则让它替换最弱的进堆,再在堆中选出新的最弱的去"守门".如果新来的元素比最弱的还弱,那它就完全不是我们要找的元素,可以直接把它pass掉.

利用这种方式选出top-k,当数据量大到可以忽略建堆以及后续调整堆部分的操作带来的时间复杂度时,我们可以近似的认为这个算法的时间复杂度为O(n).