文章目录
- 什么是并查集?
- 并查集的模拟实现
- 并查集的应用
- 省份数量
- 等式方程的可满足性
本篇总结的是并查集的使用方法和运用
什么是并查集?
给定这样一个场景,n个不同的元素划分成不同的,不相交的集合,在开始的时候,每个元素都是一个集合,经过一些规则后把这些集合进行适当的划分,此时要查询某个元素是属于哪个集合,这样的抽象数据类型就叫做并查集
来一个具体的例子,假设现在有10个人,现在每个人各自是一个小组,那么现在就有10个小组,用一个数组来表示这10个人,每个人都是一个单独的小格子
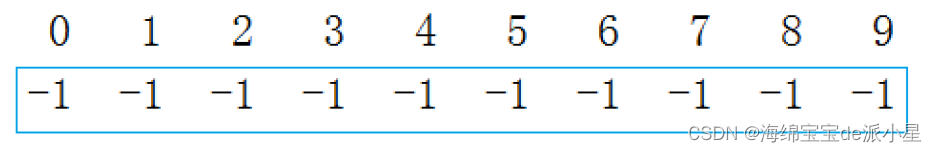
现在由于要减少管理的成本,因此要对这些人进行合并,原本是十个组,现在要变成三个组,那么就要选出来三个人作为组长代领其余的人进行各种工作,那么就可以表示成这样
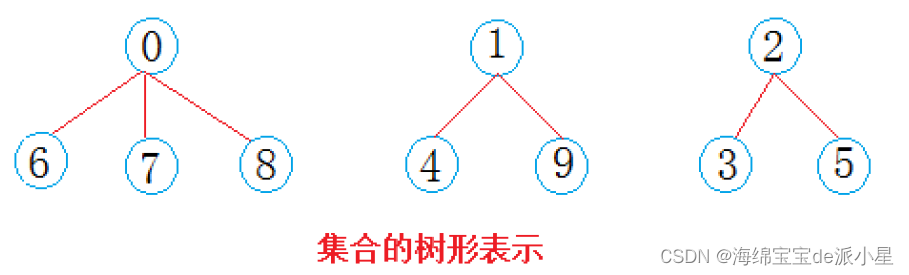
那如何用数组进行表示呢?下面给出了其中一种表示的方法
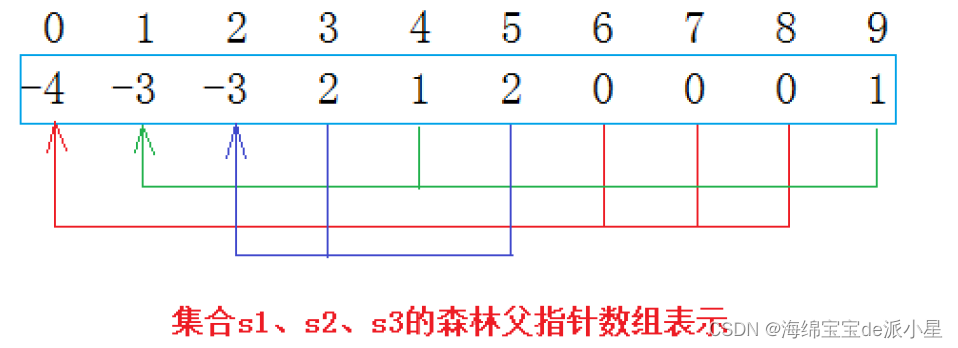
简单来说,数组的下标对应的是集合中元素的编号,如果数组是负数,那么首先说明这是根,其次数字代表的是集合中元素的个数,如果数组是一个非负数,那么这个数字代表的就是父亲所在的数组的下标
现在又出现了意外情况,三个小组又要进行合并了,那么此时如何进行合并?很简单,只需要让组长变成另外一个组的组员即可,他所代领的组员就会变成另外一个组的组员
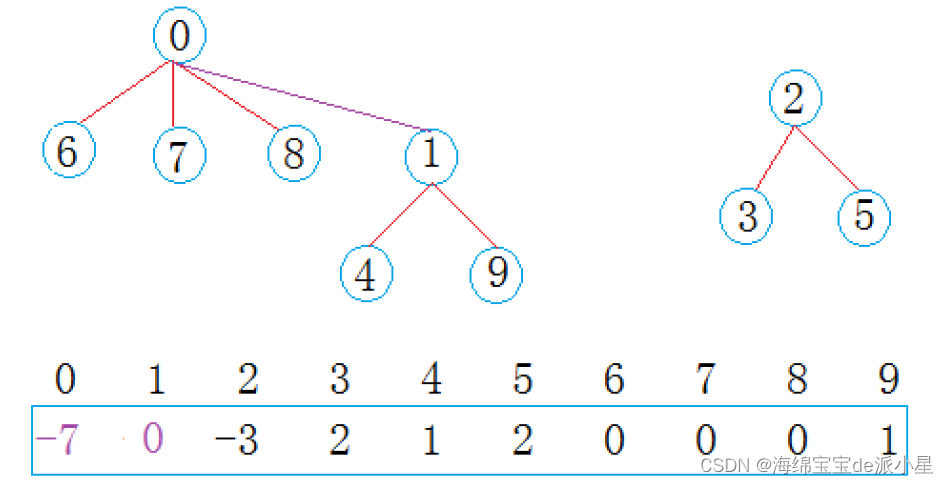
上面的这个过程,就描述了并查集所需要的各种功能和所能完成的各种任务,一般而言,并查集需要具备解决下面这些问题的能力:
- 查找元素属于哪个集合
- 查看两个元素是不是一个集合
- 两个集合合并成一个集合
- 集合的个数
那么基于上面的这四个功能,下面来模拟实现一下并查集
并查集的模拟实现
#pragma once
class UnionFindSet
{
public:
UnionFindSet(int nums)
:_ufs(nums, -1)
{}
// 查找元素属于哪个集合
int find(int root)
{
while (_ufs[root] >= 0)
{
int parent = _ufs[root];
root = parent;
}
return root;
}
// 查看两个元素是否是一个集合
bool IsSame(int x1, int x2)
{
int root1 = find(x1);
int root2 = find(x2);
return root1 == root2;
}
// 将两个集合合并成一个集合
void merge(int x1, int x2)
{
int root1 = find(x1);
int root2 = find(x2);
// 把小的集合合并到大的集合里面
if (abs(_ufs[root1]) < abs(_ufs[root2]))
swap(root1, root2);
if (root1 != root2)
{
_ufs[root1] += _ufs[root2];
_ufs[root2] = root1;
}
}
// 集合的个数
size_t GetSize()
{
int size = 0;
for (auto e : _ufs)
if (e < 0)
size++;
return size;
}
private:
// 底层就是一个数组
vector<int> _ufs;
};
并查集的应用
省份数量

首先一个最简便的方法,就是直接用已经实现的并查集套一下即可
class UnionFindSet
{
public:
UnionFindSet(int nums)
:_ufs(nums, -1)
{}
// 查找元素属于哪个集合
int find(int root)
{
while (_ufs[root] >= 0)
{
int parent = _ufs[root];
root = parent;
}
return root;
}
// 查看两个元素是否是一个集合
bool IsSame(int x1, int x2)
{
int root1 = find(x1);
int root2 = find(x2);
return root1 == root2;
}
// 将两个集合合并成一个集合
void merge(int x1, int x2)
{
int root1 = find(x1);
int root2 = find(x2);
// 把小的集合合并到大的集合里面
if (abs(_ufs[root1]) < abs(_ufs[root2]))
swap(root1, root2);
if (root1 != root2)
{
_ufs[root1] += _ufs[root2];
_ufs[root2] = root1;
}
}
// 集合的个数
size_t GetSize()
{
int size = 0;
for (auto e : _ufs)
if (e < 0)
size++;
return size;
}
private:
// 底层就是一个数组
vector<int> _ufs;
};
class Solution
{
public:
int findCircleNum(vector<vector<int>>& isConnected)
{
UnionFindSet ufs(isConnected.size());
// 利用并查集来解题
for(int i = 0; i < isConnected.size(); i++)
{
for(int j = 0; j < isConnected[i].size(); j++)
{
// 表示这这两个之间应建立关系
if(isConnected[i][j] == 1)
{
ufs.merge(i, j);
}
}
}
return ufs.GetSize();
}
};
当然也可以使用lambda表达式进行一个对象的调用
class Solution
{
public:
int findCircleNum(vector<vector<int>>& isConnected)
{
vector<int> ufs(isConnected.size(), -1);
auto findroot = [&ufs](int x)
{
while (ufs[x] >= 0)
x = ufs[x];
return x;
};
// 利用并查集来解题
for(int i = 0; i < isConnected.size(); i++)
{
for(int j = 0; j < isConnected[i].size(); j++)
{
// 表示这这两个之间应建立关系
if(isConnected[i][j] == 1)
{
int root1 = findroot(i);
int root2 = findroot(j);
if (root1 != root2)
{
ufs[root1] += ufs[root2];
ufs[root2] = root1;
}
}
}
}
int size = 0;
for (auto e : ufs)
if (e < 0)
size++;
return size;
}
};
等式方程的可满足性

class Solution
{
public:
bool equationsPossible(vector<string>& equations)
{
vector<int> ufs(26, -1);
auto findroot = [&ufs](int x)
{
while(ufs[x] >= 0)
x = ufs[x];
return x;
};
// 第一遍把相等的值放到一个集合里面
for(auto& str : equations)
{
if(str[1] == '=')
{
int root1 = findroot(str[0] - 'a');
int root2 = findroot(str[3] - 'a');
if(root1 != root2)
{
ufs[root1] += ufs[root2];
ufs[root2] = root1;
}
}
}
// 第二遍看看有没有相悖的情况
for(auto& str : equations)
{
if(str[1] == '!')
{
int root1 = findroot(str[0] - 'a');
int root2 = findroot(str[3] - 'a');
if(root1 == root2)
return false;
}
}
return true;
}
};