目录
前言:
以后我们要学map,set,AVL,红黑数所以必须要有二叉搜索数做铺垫
1、二叉搜索树概念
2.二叉搜索树操作
1.二叉搜索树的查找
a、从根开始比较,查找,比根大则往右边走查找,比根小则往左边走查找。
2. 二叉搜索树的插入
3.1 二叉搜索树的删除(一)
3.2 二叉搜索树的删除(二)
4. 二叉搜索树的应用
前言:
以后我们要学map,set,AVL,红黑数所以必须要有二叉搜索数做铺垫
1、二叉搜索树概念
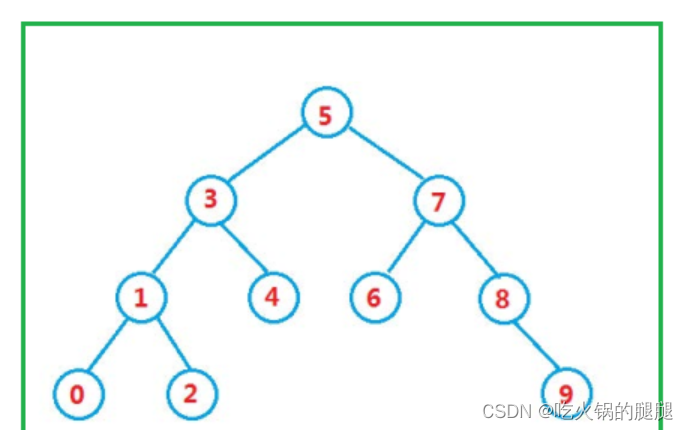
- 二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树。
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值。
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值。
- 它的左右子树也分别为二叉搜索树。
2.二叉搜索树操作
1.二叉搜索树的查找
a、从根开始比较,查找,比根大则往右边走查找,比根小则往左边走查找。
b、最多查找高度次,走到到空,还没找到,这个值不存在。

Node* Find(const K& key) //查找
{
Node* cur = _root;
while (cur)
{
if (key > cur->_key)
{
cur = cur->_right;
}
else if (key < cur->_key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return cur;
}
2. 二叉搜索树的插入
插入的具体过程如下:
a.
树为空,则直接新增节点,赋值给
root
指针
b.
树不空,按二叉搜索树性质查找插入位置,插入新节点
注意:
二叉搜索树中不能出现值相同的节点,若插入时出现值相同的节点就直接返回false,插入失败!
bool insert(const K& key)//左小右大
{
if (_root == nullptr)//第一次插入时的操作 //空树直接插入
{
_root = new Node(key);
return true;
}
//不是空树找到要寻找的位置插入
Node* cur = _root;
Node* prev = nullptr; //记录cur走过的上一个节点
while (cur != nullptr)
{
if (cur->_key < key)
{
prev = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
prev = cur;
cur = cur->_left;
}
else if (cur->_key == key)
return false;
}
cur = new Node(key);
if (prev->_key > key) //把cur节点和父节点连接起来
prev->_left = cur;
else
prev->_right = cur;
return true;
}
3.1 二叉搜索树的删除(一)
首先查找元素是否在二叉搜索树中,如果不存在,则返回
,
否则要删除的结点可能分下面四种情
况:
a. 要删除的结点无孩子结点:直接删除就可以
b. 要删除的结点只有左孩子结点:删除此节点后,将此节点直接连接到父亲节点就可以

c. 要删除的结点只有右孩子结点:也是直接删除,然后直接把节点连接到父节点上
d. 要删除的结点有左、右孩子结点:这个我们在下面分析
bool erase(const K& key)//非递归版本
{
Node* prev = nullptr;
Node* cur = _root;
while (cur != nullptr)//先找到此节点再删除
{
if (cur->_key < key)
{
prev = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
prev = cur;
cur = cur->_left;
}
else//找到了此节点后,开始删除
{
//1. 左边为空
//2. 右边为空
//3. 左右都不为空
if (cur->_left == nullptr)//左孩子为空情况
{
if (cur == _root)
_root = cur->_right;
else
{
if (cur == prev->_left)
prev->_left = cur->_right;
else
prev->_right = cur->_right;
}
delete cur;
return true;
}
else if (cur->_right == nullptr)//右孩子为空情况
{
if (cur == _root)
_root = cur->_left;
else
{
if (cur == prev->_left)
prev->_left = cur->_left;
else
prev->_right = cur->_left;
}
delete cur;
return true;
}
}
3.2 二叉搜索树的删除(二)
要删除的结点有左、右孩子结点
这里我们要找到这个节点的右子树的最小节点,把他替换要删除的节点上,然后在删除这个最小的节点,因为最小节点肯定没有左子节点(如果有,他就不是最小节点)

//注,此时的cur即为要删除的节点
Node* tmp = cur->_right;
Node* prevtmp = cur;
while (1) //寻找右子树中的最左节点
{
if (tmp->_left != nullptr)
{
prevtmp = tmp;
tmp = tmp->_left;
}
else
break;
}
cur->_key = tmp->_key;
if (tmp->_right == nullptr)//如果被替换的节点的右为空
{
if (prevtmp == cur)//被删除节点右边只有一个节点,直接将被删除节点的右置空
prevtmp->_right = nullptr;
else
prevtmp->_left = nullptr;
delete tmp;
tmp = nullptr;
}
else
{
if (prevtmp == cur)
prevtmp->_right = tmp->_right;
else
prevtmp->_left = tmp->_right;
delete tmp;
tmp = nullptr;
}
4. 二叉搜索树的应用
1.
K
模型:
K
模型即只有
key
作为关键码,结构中只需要存储
Key
即可,关键码即为需要搜索到
的值
。
比如:
给一个单词
word
,判断该单词是否拼写正确
,具体方式如下:
- 以词库中所有单词集合中的每个单词作为key,构建一棵二叉搜索树
- 在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误
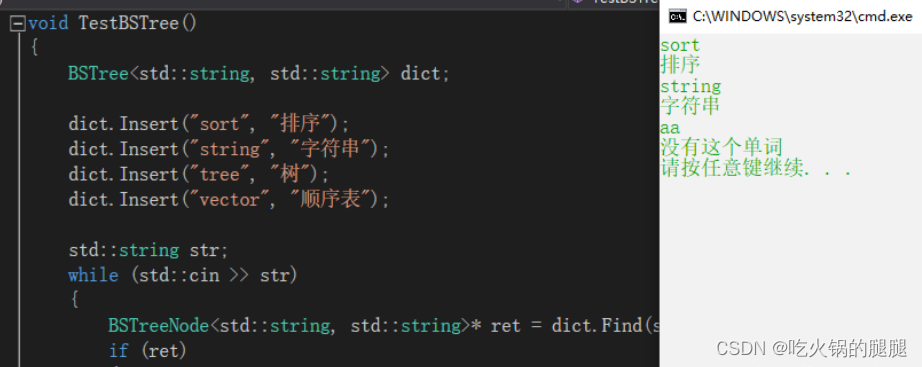
void TestBSTree()
{
BSTree<std::string, std::string> dict;
dict.Insert("sort", "排序");
dict.Insert("string", "字符串");
dict.Insert("tree", "树");
dict.Insert("vector", "顺序表");
std::string str;
while (std::cin >> str)
{
BSTreeNode<std::string, std::string>* ret = dict.Find(str); //节点的指针
if (ret)
{
std::cout << ret->_value << std::endl;
}
else
{
std::cout << "没有这个单词" << std::endl;
}
}
}
2.
KV
模型:每一个关键码
key
,都有与之对应的值
Value
,即
<Key, Value>
的键值对
。该种方
式在现实生活中非常常见:
- 比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英
文单词与其对应的中文<word, chinese>
就构成一种键值对;
- 再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数,单词与其出
现次数就是<word, count>
就构成一种键值对
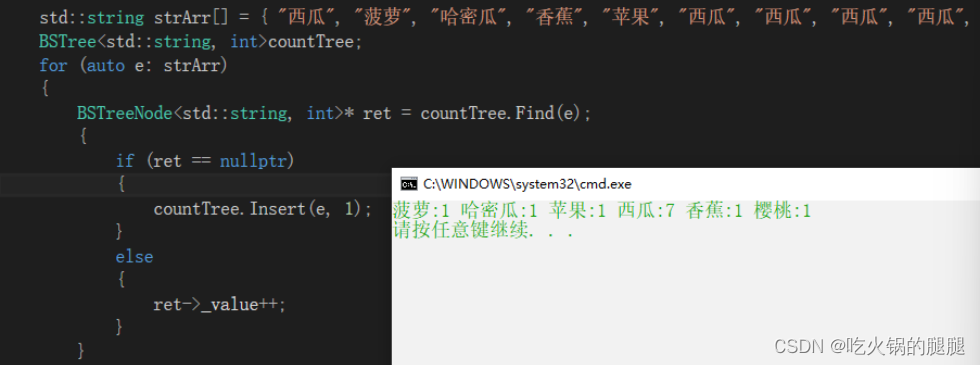
void TestBSTree()
{
std::string strArr[] = { "西瓜", "菠萝", "哈密瓜", "香蕉", "苹果", "西瓜", "西瓜", "西瓜", "西瓜", "西瓜", "西瓜", "樱桃" };
BSTree<std::string, int>countTree;
for (auto e: strArr)
{
BSTreeNode<std::string, int>* ret = countTree.Find(e);
{
if (ret == nullptr)
{
countTree.Insert(e, 1);
}
else
{
ret->_value++;
}
}
}
countTree.InOrder();
}
以上就是今天的内容分享感谢各位的收看!!!



![微服务中如何保证接口的安全性?[基于DDD和微服务的开发实战]](https://img-blog.csdnimg.cn/img_convert/82c853a8bdc86e1d7bb031d3dbe4af47.png)