矩阵和数字相乘
就是矩阵里面每个元素跟这个数字乘一遍,无论是点乘还是叉乘,对于这个都一样。

>> A=ones(3)
A =
1 1 1
1 1 1
1 1 1
>> 10*A
ans =
10 10 10
10 10 10
10 10 10矩阵和矩阵叉乘
能不能相乘,需要前面矩阵的列数等于后面矩阵的行数,出来的矩阵大小是前面矩阵的行数*后面矩阵的列数。

所以大家会发现,矩阵相乘如果前后调转了,结果会完全不一样,阴差阳错地乘出个逆矩阵出来。
有个很形象的图
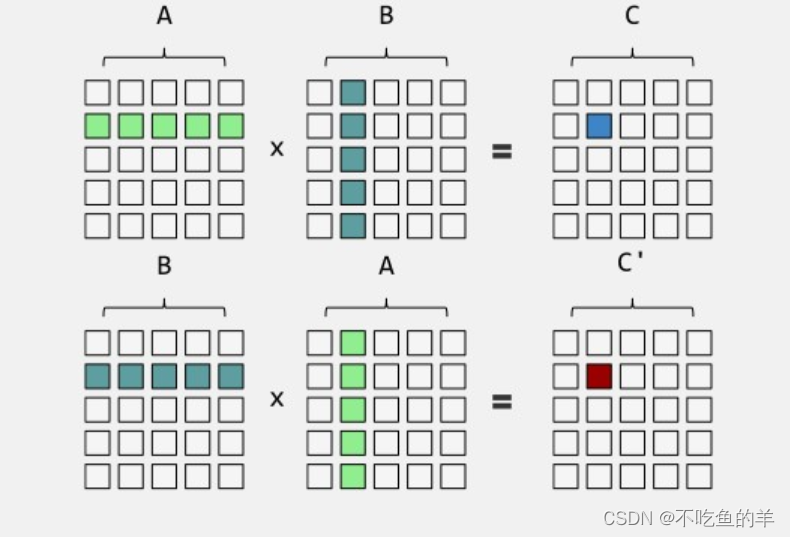
有些教材会把这个称为左乘和右乘,但是本质上其实就是矩阵相乘的先后顺序。
>> A=[1 2 3; 4 5 6;7 8 9]
A =
1 2 3
4 5 6
7 8 9
>> B=[10 20 30;40 50 60;70 80 90]
B =
10 20 30
40 50 60
70 80 90
>> A*B
ans =
300 360 420
660 810 960
1020 1260 1500
矩阵和矩阵点乘
点乘运算指将两矩阵中相同位置的元素进行相乘运算,所以需要矩阵维数和行列数都一样
>> A=[1 2 3; 4 5 6;7 8 9]
A =
1 2 3
4 5 6
7 8 9
>> B=[10 20 30;40 50 60;70 80 90]
B =
10 20 30
40 50 60
70 80 90
>> A.*B
ans =
10 40 90
160 250 360
490 640 810矩阵和数字相除
只有矩阵除以数字,没有数字除以矩阵。跟相乘一样,每个元素除以数字即可。
C =
10 40 90
160 250 360
490 640 810
>> C/10
ans =
1 4 9
16 25 36
49 64 81
>> C./10
ans =
1 4 9
16 25 36
49 64 81矩阵和矩阵除法
一般老师不让学生学除法具体怎么算,太反人类了,大家只需要记得A/B=A*inv(B)就行。当然啦,既然换成了乘法,也要注意取逆之后的两个矩阵的行列数能不能乘起来。
所谓左除右除,就是被除数和除数位置调转而已。
>> A=[1,3,5;3,4,5;2,4,8]
A =
1 3 5
3 4 5
2 4 8
>> B=[2,5,8;3,7,2;5,3,2]
B =
2 5 8
3 7 2
5 3 2
>> A/B
ans =
0.6395 -0.0058 -0.0523
0.5233 0.0407 0.3663
1.0233 -0.2093 0.1163
>> A*inv(B)
ans =
0.6395 -0.0058 -0.0523
0.5233 0.0407 0.3663
1.0233 -0.2093 0.1163矩阵和矩阵点除
也就是元素一一对应相除
>> A=[1,3,5;3,4,5;2,4,8]
A =
1 3 5
3 4 5
2 4 8
>> B=[2,5,8;3,7,2;5,3,2]
B =
2 5 8
3 7 2
5 3 2
>> A./B
ans =
0.5000 0.6000 0.6250
1.0000 0.5714 2.5000
0.4000 1.3333 4.0000dot点乘/内积/点积/数量积
dot(A,B,X)入参X 为1表示按列,为2表示按行,默认按列。算法如下
A=[a1 a2 a3;a4 a5 a6]
B=[b1 b2 b3;b4 b5 b6]
C=[c1 c2 c3]
D=[d1 d2 d3]
dot(A,B)=dot(A,B,1)%按列(每列合在一起变成一行)
=[a1*b1+a4*b4,a2*b2+a5*b5,a3*b3+a6*b6]
dot(A,B,2)%按行(每行合在一起变成一列)
=[a1*b1+a2*b2+a3*b3;a4*b4+a5*b5+a6*b6]
dot(C,D)=dot(D,C)=dot(inv(C),D)%如果是向量,无论方向,合起来变成一个标量
=c1*d1 + c2*d2 + c3*d3 例子如下
%矩阵
>> A=[1 2 3; 4 5 6;7 8 9]
A =
1 2 3
4 5 6
7 8 9
>> B=[10 20 30;40 50 60;70 80 90]
B =
10 20 30
40 50 60
70 80 90
>> dot(A,B,1)
ans =
660 930 1260
>> dot(A,B,2)
ans =
140
770
1940
%向量
>> A=[2 4 6 8]
A =
2 4 6 8
>> B=[3 4 5 6]
B =
3 4 5 6
>> dot(A,B)
ans =
100cross叉积/向量积/矢量积
这个就比较复杂了,要求也多:
1、相乘的两个对象行列相同
2、至少有一个维度的长度是3,也就是要么3行要么3列
算法如下
A=[a1 a2 a3;
a4 a5 a6]
B=[b1 b2 b3;
b4 b5 b6]
cross(A,B)=
[(a2*b3 - a3*b3),(a3*b1 - a1*b3),(a1*b2 - a2*b1);
(a5*b6 - a6*b5),(a6*b4 - a4*b6),(a4*b5 - a5*b4)]举个例子
>> A=[1 2 3]
A =
1 2 3
>> B=[4 5 6]
B =
4 5 6
>> cross(A,B)
ans =
-3 6 -3
>> C=[1 2 3;4 5 6]
C =
1 2 3
4 5 6
>> D=[30 20 10;60 50 40]
D =
30 20 10
60 50 40
>> cross(C,D)
ans =
-40 80 -40
-100 200 -100