逻辑回归原理
线性回归主要用于预测连续的数值输出,基于线性关系模型,其目标是最小化实际值和预测值之间的差异。
逻辑回归主要用于分类问题,尤其是二元分类,它预测属于某一类别的概率,并基于概率输出进行决策,使用的是逻辑(Sigmoid)函数将线性模型的输出转换为概率值。简单说就是:找到一组参数,使得模型对分类结果的预测概率最大化。
举个例子:在预测银行贷款这件事上,线性回归可以帮你预测银行能发放的贷款额度是多少,逻辑回归则是尽可能准确地预测银行能否发放贷款(要么0,要么1)。
在线性回归中,我们着力于在U型曲线里找到局部最低点,以最小损失形成模型去预测结果。而在逻辑回归中,我们着力于最大化似然函数,这通常意味着找到一组参数,使得给定数据集中观测到的分类结果出现的概率最大。这个过程可以视为通过调整模型参数来提高正确分类的概率,从而在概率空间中寻找最优解。简单说:在逻辑回归中,我们致力于找到参数设置,使得模型对数据进行正确分类的可能性最大化。
对于最简单的逻辑回归,我们可以通过Sigmoid函数表示为下图,当预测值>0.5的时候预测结果为1。
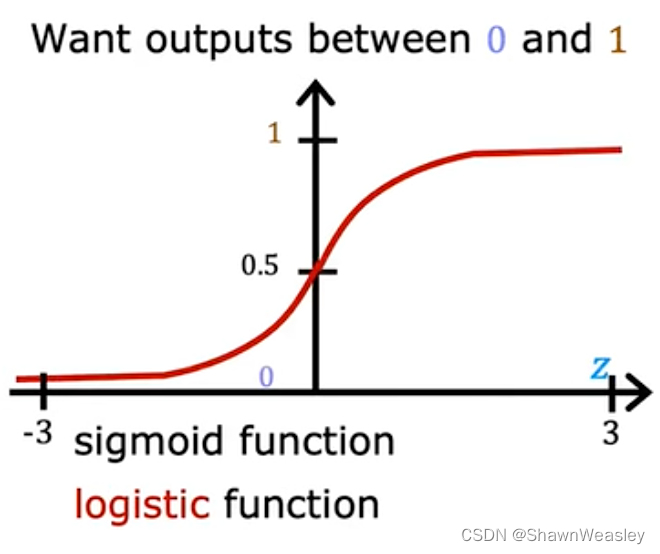
在线性回归中,我们使用特征的加权和:
z
=
β
0
+
β
1
x
1
+
β
2
x
2
+
.
.
.
+
β
n
x
n
z = \beta_0 + \beta_1x_1 + \beta_2x_2 + ... + \beta_nx_n
z=β0+β1x1+β2x2+...+βnxn来代表最终预期得到的函数,而在逻辑回归中,要得到如上图的Sigmoid函数,我们就要使用
σ
(
z
)
=
1
1
+
e
−
(
β
0
+
β
1
x
1
+
β
2
x
2
+
.
.
.
+
β
n
x
n
)
\sigma(z) = \frac{1}{1 + e^{-(\beta_0 + \beta_1x_1 + \beta_2x_2 + ... + \beta_nx_n)}}
σ(z)=1+e−(β0+β1x1+β2x2+...+βnxn)1缩写为:
σ
(
z
)
=
1
1
+
e
−
z
\sigma(z) = \frac{1}{1 + e^{-z}}
σ(z)=1+e−z1其中,
e
e
e是自然对数的底数,约等于2.71828。因此Sigmoid函数的输出值始终位于0和1之间。这个特性使得Sigmoid函数非常适合用于将任意实数值映射为概率。
Sigmoid函数是一个非线性函数。这意味着使用Sigmoid函数可以帮助模型学习非线性关系,这是线性模型所做不到的。
如下图,逻辑回归需要计算出一个函数,来区分该值等于1的概率
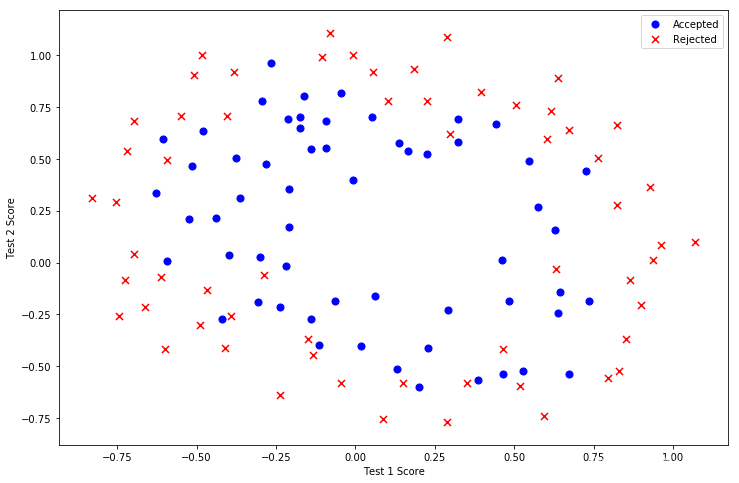
有可能最终的结果就类似于下面的绿线范围,范围内的为1,外的为0
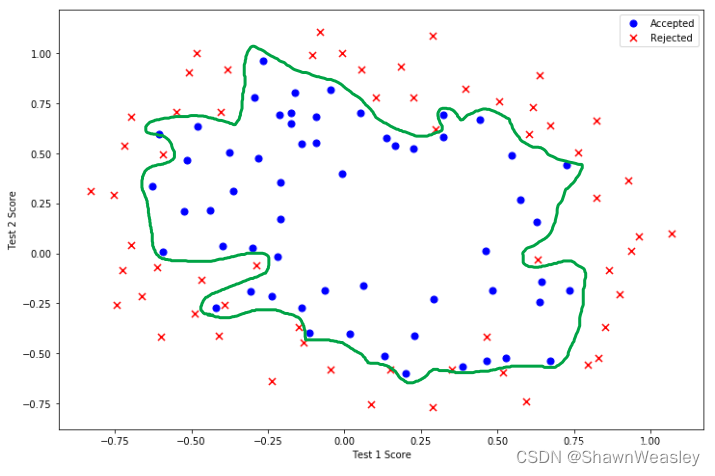
在逻辑回归中的似然函数用来评估模型参数
θ
\theta
θ的效果:
L
(
θ
)
=
∏
i
=
1
n
p
(
y
(
i
)
∣
x
(
i
)
;
θ
)
L(\theta) = \prod_{i=1}^{n} p(y^{(i)}|x^{(i)};\theta)
L(θ)=i=1∏np(y(i)∣x(i);θ) 它是给定参数
θ
\theta
θ下,产生观察到的数据集的概率。似然函数的目标是找到最佳的参数集
θ
\theta
θ,使得观测到的数据出现的概率最大。
在逻辑回归中,这个概率
p
(
y
∣
x
;
θ
)
p(y|x;\theta)
p(y∣x;θ)就是由Sigmoid函数计算出来的。
简单来说,Sigmoid函数提供了一种机制来预测事件发生的概率,而似然函数则用这些概率来评估模型参数的好坏。在训练过程中,我们通过调整参数 θ \theta θ最大化似然函数(梯度上升),寻找能够最好地解释观测数据的模型参数。
所以从核心方法上来说,无论是线性回归还是逻辑回归都是在找到一组参数使得某个目标函数达到最优。
逻辑回归代码
逻辑回归示例代码如下:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.optimize as opt
# 导入数据并添加列名
data = pd.read_csv('ex2data1.txt', header=None, names=['Exam 1', 'Exam 2', 'Admitted'])
# 绘制散点图
def plot_data(data):
positive = data[data['Admitted'] == 1]
negative = data[data['Admitted'] == 0]
plt.figure(figsize=(12,8))
plt.scatter(positive['Exam 1'], positive['Exam 2'], s=50, c='b', marker='o', label='Admitted')
plt.scatter(negative['Exam 1'], negative['Exam 2'], s=50, c='r', marker='x', label='Not Admitted')
plt.legend()
plt.xlabel('Exam 1 Score')
plt.ylabel('Exam 2 Score')
plt.show()
plot_data(data)
# 定义sigmoid函数
def sigmoid(z):
return 1 / (1 + np.exp(-z))
# 定义代价函数
def cost(theta, X, y):
theta = np.matrix(theta)
first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T)))
return np.sum(first - second) / len(X)
# 定义梯度函数
def gradient(theta, X, y):
theta = np.matrix(theta)
error = sigmoid(X * theta.T) - y
return ((X.T * error) / len(X)).T
# 数据预处理
data.insert(0, 'Ones', 1)
X = data.iloc[:, :-1].values
y = data.iloc[:, -1:].values
theta = np.zeros(X.shape[1])
# 使用优化函数找到最优参数
result = opt.fmin_tnc(func=cost, x0=theta, fprime=gradient, args=(X, y))
# 定义预测函数
def predict(theta, X):
probability = sigmoid(np.dot(X, theta))
return [1 if x >= 0.5 else 0 for x in probability]
# 计算准确率
theta_min = np.array(result[0])
predictions = predict(theta_min, X)
correct = [1 if a == b else 0 for (a, b) in zip(predictions, y.flatten())]
accuracy = sum(correct) / len(correct)
print('Accuracy = {}%'.format(accuracy * 100))
"""
绘制决策边界
"""
def plot_decision_boundary(data, theta):
# 绘制原始数据的散点图
positive = data[data['Admitted'].isin([1])]
negative = data[data['Admitted'].isin([0])]
plt.figure(figsize=(12,8))
plt.scatter(positive['Exam 1'], positive['Exam 2'], s=50, c='b', marker='o', label='Admitted')
plt.scatter(negative['Exam 1'], negative['Exam 2'], s=50, c='r', marker='x', label='Not Admitted')
# 添加决策边界
x_value = np.array([np.min(X[:,1]), np.max(X[:,1])])
y_value = -(theta[0] + theta[1]*x_value) / theta[2]
plt.plot(x_value, y_value, 'g', label='Decision Boundary')
plt.xlabel('Exam 1 Score')
plt.ylabel('Exam 2 Score')
plt.legend()
plt.show()
# 使用最优化的theta绘制决策边界
plot_decision_boundary(data, result[0])
输出后的结果:
| NIT(迭代次数) | NF(函数评估次数) | F(代价函数的值) | GTG(梯度的平方和) |
|---|---|---|---|
| 0 | 1 | 6.931471805599453E-01 | 2.71082898E+02 |
| 1 | 3 | 6.318123602631673E-01 | 7.89087138E-01 |
| 2 | 5 | 5.892425284546917E-01 | 7.39225968E+01 |
| 3 | 7 | 4.227824467516530E-01 | 1.85266404E+01 |
| 4 | 9 | 4.072926898646252E-01 | 1.68671176E+01 |
| 5 | 11 | 3.818855078923481E-01 | 1.07734992E+01 |
| 6 | 13 | 3.786234920021553E-01 | 2.31584985E+01 |
| 7 | 16 | 2.389267774352392E-01 | 3.00820981E+00 |
| 8 | 18 | 2.047203844871719E-01 | 1.52224659E-01 |
| 9 | 20 | 2.046713871134023E-01 | 6.62490915E-02 |
| 10 | 22 | 2.035303175123319E-01 | 9.30774264E-04 |
| 11 | 24 | 2.035293534076603E-01 | 8.07450037E-06 |
| 12 | 26 | 2.035251130726250E-01 | 1.80180151E-04 |
| 13 | 28 | 2.034984116011556E-01 | 5.02836428E-04 |
| 14 | 30 | 2.034978388892823E-01 | 9.96725740E-06 |
| 15 | 32 | 2.034977911359196E-01 | 3.79191989E-06 |
| 16 | 34 | 2.034977391259835E-01 | 1.95701962E-05 |
| 17 | 36 | 2.034977015894753E-01 | 2.30450436E-13 |
NIT:迭代次数,表示优化过程中总共执行了多少次迭代。
NF:函数评估次数,即目标函数(在这种情况下是代价函数)计算了多少次。
F:代价函数的值,即当前参数下的代价。
GTG:梯度的平方和,用于评估优化的进度和停止条件。
模型预测正确率Accuracy = 89.0%
基于本数据的决策边界图:
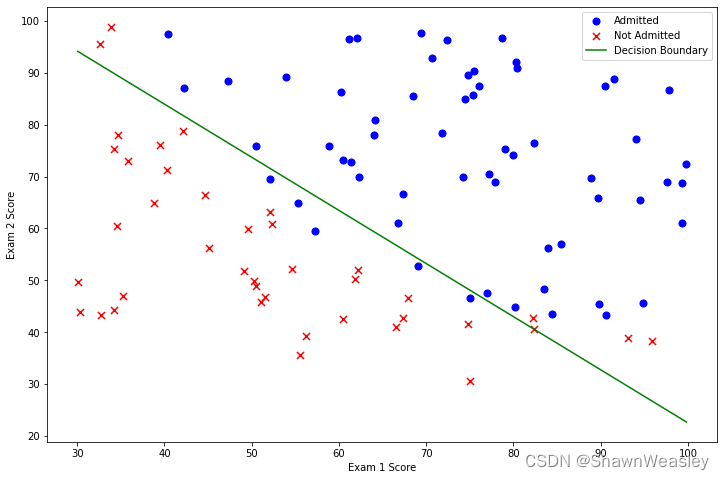
注:本文为学习吴恩达版本机器学习教程的代码整理,使用的数据集为https://github.com/fengdu78/Coursera-ML-AndrewNg-Notes/blob/f2757f85b99a2b800f4c2e3e9ea967d9e17dfbd8/code/ex2-logistic%20regression/ex2data1.txt